Bài toán xâu con chung dài nhất là một bài toán quan trọng trong lĩnh vực xử lý xâu. Nhiều ứng dụng thực tế sử dụng bài toán này để tìm ra xâu con chung lớn nhất giữa các xâu khác nhau. Không nên nhầm lẫn giữa bài toán này với bài toán chuỗi con chung dài nhất.
Ví dụ
Ví dụ với ba xâu "ABAB", "BABA" và "ABBA": Xâu con chung dài nhất là các xâu "AB" và "BA" với độ dài bằng 2. Các xâu con khác có độ dài ngắn hơn là "A" và "B".
Định nghĩa bài toán
- Định nghĩa: Cho hai xâu S độ dài m và xâu T độ dài n, tìm xâu có độ dài lớn nhất là xâu con của cả hai xâu S và T.
- Tổng quát hóa bài toán này là bài toán tìm xâu con k-chung (k-common substring problem): Cho một tập xâu S = { S1, ..., SK }, trong đó | Si | = ni và Σ ni = N. Với mỗi giá trị k thỏa mãn 2 ≤ k ≤ K, tìm các xâu con chung dài nhất của ít nhất k xâu.
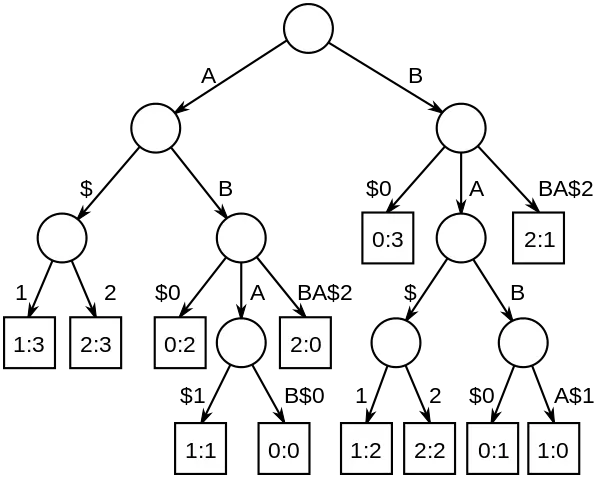
Thuật toán
Có thể tìm độ dài và vị trí bắt đầu của các xâu con dài nhất của S và T trong Θ ( n + m ) bằng cách sử dụng Cây hậu tố khái quát (Generalized suffix tree). Ngoài ra, cũng có thể giải quyết bài toán theo phương pháp Quy hoạch động với độ phức tạp Θ ( n * m ).
Cây hậu tố
Hình trên là cây hậu tố tổng quát cho các xâu "ABAB", "BABA" và "ABBA", được đánh số tương ứng 0, 1 và 2.
Quy hoạch động
Có thể tìm các hậu tố dài nhất của các tiền tố của các xâu. Hậu tố dài nhất được định nghĩa: LCSuff(S1..p, T1..q) = LCSuff(S1..p-1, T1..q-1) + 1 if S[p] = T[q] else 0.
Ví dụ với hai xâu "ABAB" và "BABA": A B A B 0 0 0 0 0 B 0 0 0 1 0 1 0 2 0 0 0 B 0 3 0 1 0 0
Hậu tố dài nhất của các tiền tố của xâu S và T chính là xâu con dài nhất của chúng. Các xâu con này được đánh dấu theo đường chéo, màu đỏ trong bảng. Ví dụ: các xâu con dài nhất là "BAB" và "ABA".
Có thể mở rộng phương pháp này để tìm xâu con dài nhất của nhiều xâu hơn nữa bằng cách đưa thêm 1 chiều vào bảng cho mỗi xâu mới.
