Bitweiser Operator – Tìm hiểu các phép toán trên bit trong lập trình

Bạn đã bao giờ nghe về "bitweiser operator" trong lập trình chưa? Trong ngành công nghệ thông tin, "bitweiser operator" là một phép toán được áp dụng trên các chuỗi bit, trường bit, dãy bit hoặc vectơ bit trên cấp độ từng bit. Đặc biệt trong các ngôn ngữ lập trình thuộc gia đình C, các số nhị phân có thể được xem như các dãy bit mà không cần các đánh dấu cú pháp bổ sung khác.

Các phép toán trên từng bit cơ bản này là những phép toán đơn giản nhất từ góc độ kỹ thuật mạch, và tất cả các phép toán cao hơn đều có thể được giảm xuống thành các phép toán này. Tuy nhiên, các phép toán "bitweiser" thường ít được ưu tiên tối ưu hóa so với các phép toán số học phức tạp hơn như cộng và trừ, vì chúng không quan trọng đối với tốc độ của hệ thống máy tính.

Phép toán "bitweiser" (bitwise operators)

Sử dụng thuật ngữ "bitweiser" cho thấy các toán hạng đa phần được xử lý thành từng thành phần. (Tất nhiên, chúng cũng có thể là đơn phần.) Đối với nhiều ngôn ngữ lập trình thuộc gia đình C, có sự phân biệt cú pháp và ý nghĩa giữa "bitwise" (nhiều phần) và "logical" (Boolean, một phần duy nhất). Vì nguy cơ nhầm lẫn có thể xảy ra, trong bài viết này, chúng tôi sẽ liệt kê cả hai loại phép toán.

Phép NOT (bitwise NOT)

Phép NOT bit (phủ định bit) hoặc Complement là một phép gắn kết một bit logic và thực hiện đảo ngược logic (đảo ngược) của mỗi bit. Nếu chuỗi bit được coi là một số nhị phân, đây là việc tạo số bù nhất định. Mỗi 0 thay thế bằng 1 và mỗi 1 thay thế bằng 0. Ví dụ:

NOT 0111 = 1000

Trong nhiều ngôn ngữ lập trình thuộc gia đình C, phép NOT bit được biểu diễn bằng dấu ~ (Tilde), trong khi toán tử NOT logic (!) được sử dụng để đại diện cho NOT logic, trong đó toàn bộ giá trị được xem như một biểu thức Boolean true (không bằng 0) hoặc false (bằng 0). NOT logic không phải là phép toán trên từng bit.

Phép AND (bitwise AND)

Phép AND bit (AND bit) được áp dụng trên hai chuỗi bit cùng độ dài và trả về một chuỗi bit có cùng độ dài bằng cách kết hợp từng bit tại cùng một vị trí (từng bit đầu tiên, từng bit thứ hai, v.v.) với một phép toán logic AND (tích logic). Đối với mỗi cặp, bit kết quả là 1 nếu cả hai bit đều là 1, ngược lại là 0. Ví dụ:

0101 AND 0011 = 0001

Trong các ngôn ngữ lập trình liên quan đến C, phép AND bit được biểu diễn bằng ký hiệu & (Dấu &), trong khi phép AND logic tương ứng, mà xem xét mỗi toán hạng của nó là một giá trị logic, được biểu diễn bằng ký hiệu && (Hai dấu &).

Phép AND bit có thể được sử dụng để áp dụng một "mặt nạ" lên một chuỗi bit. Điều này cho phép cô lập các phần của chuỗi bit, và bạn có thể xác định xem một bit cụ thể có được thiết lập hay không. Ví dụ:

0011
AND
0010
=
0010

Để xác định xem bit thứ ba có được thiết lập hay không trong chuỗi bit trên, bạn có thể áp dụng một phép AND bit với mặt nạ chứa một bit 1 tại vị trí thứ ba:

0011
AND
0100
=
0000

Phép AND bit có thể được kết hợp với phép NOT bit để xóa các bit. Ví dụ, để xóa bit thứ hai trong chuỗi bit trên, bạn có thể áp dụng một phép NOT bit với một mặt nạ có một bit 1 tại vị trí thứ hai, sau đó áp dụng một phép AND bit với chuỗi bit gốc:

0101
NOT
0010
=
1101

0101
AND
1101
=
0101

Phép OR (bitwise OR)

Phép OR bit (OR bit) được áp dụng trên hai chuỗi bit cùng độ dài và trả về một chuỗi bit cùng độ dài bằng cách kết hợp từng bit tại cùng một vị trí với một phép toán logic OR (tổng logic). Đối với mỗi cặp, bit kết quả là 0 nếu cả hai bit đều là 0, ngược lại là 1. Ví dụ:

0101 OR 0011 = 0111

Trong các ngôn ngữ lập trình liên quan đến C, phép OR bit được biểu diễn bằng dấu | (Dấu thiết lập), trong khi phép OR logic (tổng logic) tương ứng được biểu diễn bằng dấu || (Hai dấu thiết lập).

Phép OR bit được sử dụng khi nhiều bit được sử dụng như các cờ (flags). Các bit của một số nhị phân có thể đại diện cho một biến Boolean riêng biệt. Khi áp dụng phép OR bit với một số nhị phân như vậy và một "mặt nạ" chứa một bit 1 ở các vị trí cụ thể, mỗi bit trong chuỗi nhị phân kết quả sẽ được thiết lập nếu bit tương ứng hoặc bit từ trước đó tương ứng có giá trị là 1. Ví dụ:

0010
OR
1000
=
1010

Phép OR bit cũng có thể được sử dụng để tiết kiệm không gian lưu trữ khi các chương trình cần quản lý nhiều giá trị Boolean. Bằng cách áp dụng phép OR bit lên một giá trị nhị phân và một "mặt nạ" chứa một bit 1 tại các vị trí cụ thể, bạn có thể tạo ra một chuỗi bit mới trong đó các bit tại các vị trí tương ứng sẽ được thiết lập bổ sung với các bit đã có từ trước đó. Ví dụ:

0010
OR
1000
=
1010

Phép XOR (bitwise XOR)

Phép XOR bit (XOR bit) được áp dụng trên hai chuỗi bit cùng độ dài và trả về một chuỗi bit cùng độ dài bằng cách kết hợp từng bit tại cùng một vị trí với một phép toán XOR (XOR logic). Kết quả là 1 nếu hai bit tương ứng là khác nhau, trong khi kết quả là 0 nếu hai bit tương ứng là giống nhau. Ví dụ:

0101 XOR 0011 = 0110

Trong các ngôn ngữ lập trình liên quan đến C, phép XOR bit (XOR bit) được biểu diễn bằng dấu ^ (Dấu ngoại trừ), trong khi phép XOR logic tương ứng được biểu diễn bằng dấu ^^.

Phép XOR bit được sử dụng trong việc chuyển đổi hoặc đảo ngược giá trị bit của các cờ (flags). Bằng cách áp dụng phép XOR bit với một số nhị phân và một "mặt nạ" chứa các bit 1 tại các vị trí cụ thể, từng bit trong chuỗi nhị phân kết quả sẽ được chuyển đổi nếu bit tương ứng với bit từ trước đó tương ứng có giá trị là 1. Ví dụ:

0101
XOR
0011
=
0110

Phép XOR bit cũng có thể được sử dụng để chuyển đổi các cờ trong chuỗi bit. Bằng cách áp dụng phép XOR bit với một giá trị nhị phân như vậy và một "mặt nạ" chứa các bit 1 tại vị trí cụ thể, mỗi bit trong chuỗi bit kết quả sẽ được chuyển đổi nếu bit tương ứng tại vị trí đã được đặt ở 1. Ví dụ:

0101
XOR
1000
=
1101

Phép XOR bit cũng có thể được sử dụng để xoay các bit trong chuỗi bit. Bằng cách áp dụng phép XOR bit với một giá trị nhị phân như vậy và một "mặt nạ" chứa một bit 1 tại vị trí cụ thể, các bit từ bit chuyển tiếp được chuyển đổi từ 0 thành 1 và ngược lại. Ví dụ:

0101
XOR
0010
=
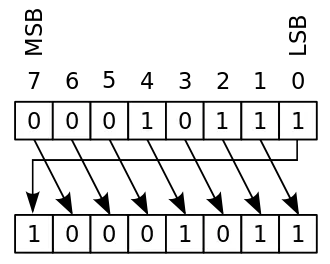
0111

Phép dịch bit (bitwise shift)

Trong các phép toán "dịch bit" (bitwise shift), các bit được coi là các ký tự đơn tại một vị trí bit cụ thể - và không phải là các cặp bit tương ứng như các phép toán trên đây. Điều này có nghĩa là việc dịch bit theo hướng toán học tạo ra một số nhị phân hoặc, trong trường hợp cụ thể hơn, một chuỗi bit (hoặc một số nhị phân không có dấu (unsigned)).

Dưới đây là bảng mô tả các phép dịch bit:

Phép dịch trái (left shift)	Phép dịch phải (right shift)

Trong các ngôn ngữ lập trình như C, C++, Java, và ARM-Assembler, phép dịch trái tương đương với việc nhân một số nhị phân với 2^n, trong khi phép dịch phải tương đương với việc chia một số nhị phân cho 2^n.

Phép dịch bit có thể được sử dụng để tính toán phần dư của một số nhị phân chia cho 2^k bằng cách dịch bit sang trái và sau đó dịch bit sang phải. Việc này đặt tất cả các bit từ vị trí thứ k trở đi từ phải sang 0. Ví dụ, 17 mod 8 = 1 tương ứng với:

010001 (17)
AND
000111 (7 = 8−1)
=
000001

Ứng dụng

Mặc dù các máy tính thường đã được tích hợp sẵn các lệnh hiệu quả để thực hiện các phép toán số học và logic, tất cả các phép toán này cũng có thể được thực hiện bằng cách kết hợp các phép toán "bitweiser" và so sánh với không. Mã giả dưới đây cho thấy cách nhân hai số nguyên tương ứng a và b chỉ bằng dịch bit và cộng:

c := 0
WHILE b ≠ 0
    IF (b AND 1) ≠ 0
        c := c + a
    shift a left by 1
    shift b right by 1
RETURN c

Đoạn mã này thực hiện một phép nhân nhị phân theo cách viết từ cuối lên đầu (bắt đầu từ chữ số cuối cùng của b).