Các Bài Toán về Khoảng Cách trong Không Gian và Cách Giải

Hãy cùng tìm hiểu về một số bài toán thú vị về khoảng cách trong không gian và cách giải chúng. Đây là những bài toán quan trọng trong môn Toán 12 giúp bạn nắm vững lý thuyết và biết cách làm bài tập. Đồng thời, nắm bắt được các kỹ năng giải quyết vấn đề để đạt kết quả cao trong các bài thi.

Các Bài Toán về Khoảng Cách trong Không Gian

I. LÝ THUYẾT

1. Khoảng cách từ một điểm đến một mặt phẳng, đến một đường thẳng.

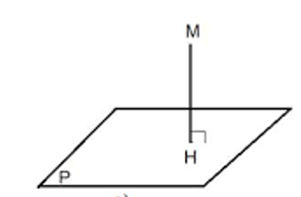
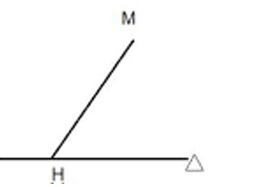
Khoảng cách từ một điểm M đến một mặt phẳng (P) hoặc đến đường thẳng ∆ là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên mặt phẳng (P) hoặc trên đường thẳng ∆.

• Kí hiệu khoảng cách từ M đến (P) là d(M, (P))

• Kí hiệu khoảng cách từ M đến ∆ là d(M, ∆)

2. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song.

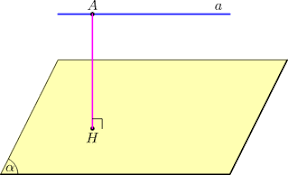
a) Khoảng cách giữa đường thẳng a và mặt phẳng (α) song song với a là khoảng cách từ một điểm bất kỳ của a tới mặt phẳng (α) cụ thể d(a,(α)) = d (A,(α)) với A thuộc a.

Ta có: d(a, (α)) = d(A, (α)) = AH

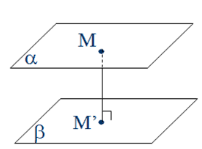
b) Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kỳ của mặt phẳng này tới mặt phẳng kia, cụ thể d((α),(β)) = d(M,(β)) với M thuộc mặt phẳng (α).

3. Khoảng cách giữa hai đường thẳng chéo nhau

Đường thẳng MN cắt và vuông góc với cả a và b gọi là đường vuông góc chung của a và b.

Khoảng cách giữa hai đường thẳng chéo nhau bằng độ dài đoạn vuông góc chung của hai đường thẳng chéo nhau đó. Cụ thể: d (a, b) = MN.

II. PHƯƠNG PHÁP GIẢI VÀ VÍ DỤ MINH HỌA

1. Khoảng cách từ một điểm đến mặt phẳng.

Phương pháp giải: Khoảng cách từ M0(x0;y0;z0) đến mặt phẳng (P): Ax + By + Cz + D = 0 là:

Ví dụ 1: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x + 2y - 2z + 5 = 0 và điểm M (0; 2; 4). Tính d (M; (P)).

Hướng dẫn giải: Ta có . Chọn A.

2. Khoảng cách giữa hai mặt phẳng song song.

Phương pháp giải: Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm thuộc mặt phẳng này đến mặt phẳng kia. Cụ thể, để tính khoảng cách giữa hai mặt phẳng song song (P) và (Q) ta thực hiện các bước như sau: +) Lấy điểm M thuộc mặt phẳng (P). +) Tính khoảng cách từ điểm M đến mặt phẳng (Q) (áp dụng công thức khoảng cách từ một điểm đến mặt phẳng).

Hướng dẫn giải: Ví dụ 2: Khoảng cách giữa hai mặt phẳng song song (P): 4x - 3y + z - 2 = 0 và (Q): 12x - 9y + 3z + 1 = 0 là

Hướng dẫn giải: Lấy điểm M(0;0;2) ∈ (P). Chọn D.

3. Khoảng cách từ một điểm đến một đường thẳng

Phương pháp giải: Khoảng cách từ điểm M đến một đường thẳng d đi qua điểm A có vectơ chỉ phương được xác định bởi công thức:

Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz khoảng cách từ điểm M (2; 0; 1) đến đường thẳng là

Hướng dẫn giải: Đường thẳng d đi qua A (1; 0; 2) có một vectơ chỉ phương là . Ta có: . Suy ra Khoảng cách từ điểm M (2; 0; 1) đến đường thẳng là:

Chọn C.

4. Khoảng cách giữa hai đường thẳng song song

Phương pháp giải: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia. Cụ thể, để tính khoảng cách giữa hai đường thẳng song song d và d’ ta thực hiện như sau: +) Lấy M thuộc đường thẳng d. +) Tính khoảng cách từ M đến đường thẳng d’ (bằng công thức khoảng cách từ một điểm đến một đường thẳng).

Ví dụ 4: Trong không gian Oxyz cho hai đường thẳng có phương trình lần lượt là. Tính khoảng cách giữa hai đường thẳng đó.

Hướng dẫn giải: Ta lấy M (1; 2; 3) thuộc đường thẳng d1 . Ta có d2 đi qua A (3; 2; 5) và có một vectơ chỉ phương là . Khi đó: Vì d1,d2 song song nên ta có:

5. Khoảng cách giữa hai đường thẳng chéo nhau:

Phương pháp giải: d đi qua điểm A và có vectơ chỉ phương và d’ đi qua điểm B và có vectơ chỉ phương là:

Ví dụ 5: Tính khoảng cách giữa hai đường thẳng chéo nhau.

Hướng dẫn giải: Đường thẳng d1 có vectơ chỉ phương là và đi qua điểm M1 (7;-1;0) . Đường thẳng d2 có vectơ chỉ phương là và đi qua điểm M2 (-2;2;3). Ta có:

Khoảng cách giữa hai đường thẳng d1 và d2 là

Chọn D.

6. Khoảng cách giữa đường thẳng d song song với mặt phẳng (P)

Phương pháp giải: Khoảng cách giữa đường thẳng d song song với mặt phẳng (P) là khoảng cách từ một điểm M thuộc đường thẳng d đến mặt phẳng (P), cụ thể:

Ví dụ 6: Trong không gian Oxyz, cho đường thẳng và mặt phẳng (P): x + 2y - 2z + 1 = 0. Khoảng cách giữa đường thẳng d và mặt phẳng (P) bằng

Hướng dẫn giải: Đường thẳng d đi qua M (1; 0; -3) và nhậnlàm véc tơ chỉ phương. Mặt phẳng (P) nhậnlàm véc tơ pháp tuyến. Ta có Vậy

Chọn B.

III. BÀI TẬP ÁP DỤNG

Câu 1: Trong không gian Oxyz, khoảng cách từ điểm A (1; 2; 2) đến mặt phẳng (α) : x + 2y - 2z - 4 = 0 bằng:

Câu 2: Tính khoảng cách giữa hai mặt phẳng song song (P): 2x - y - 2z - 4 = 0 và (Q): 2x - y - 2z = 2 = 0.

Câu 3: Tính khoảng cách giữa mặt phẳng (P): 2x - y - 2z - 4 = 0 và đường thẳng

Câu 4: Khoảng cách từ điểm E (1; 1; 3) đến đường thẳng bằng

Câu 5: Trong không gian Oxyz khoảng cách từ điểm M (3; -4; 1) tới mặt phẳng (Oyz) bằng

A. 1. B. 14. C. 4. D. 3.

Câu 6: Tính khoảng cách h từ điểm A (2; 1; 4) đến đường thẳng

Câu 7: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 2z + m = 0 và điểm A (1; 1; 1). Khi đó m nhận giá trị nào sau đây để khoảng cách từ điểm A đến mặt phẳng (P) bằng 1?

A. -2. B. -8. C. -2 hoặc - 8. D. 3.

Câu 8: Trong không gian Oxyz, khoảng cách từ điểm M (1; 3; 2) đến đường thẳng là

Câu 9: Khoảng cách giữa hai đường thẳng chéo nhau là

Câu 10: Tính khoảng cách giữa hai đường thẳng chéo nhau

ĐÁP ÁN

Câu 1 2 3 4 5 6 7 8 9 10 Đáp án B A B D D C C C C D

IV. BÀI TẬP TỰ LUYỆN

Bài 1. Tính khoảng cách giữa hai mặt phẳng song song (P): 4x - 3y + z - 2 = 0 và (Q): 12x - 9y + 3z + 1 = 0.

Bài 2. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (Q): x + 2y - 3z + 5 = 0 và điểm M (0; 1; 2). Tính d (M; (Q)).

Bài 3. Trong không gian với hệ trục tọa độ Oxyz. Tính khoảng cách từ điểm M (2;0;1) đến đường thẳng d: x−12=y1=z+23.

Bài 4. Tính khoảng cách giữa hai đường thẳng chéo nhau d1: x−73=y+12=z−5 và d2: x=−2−ty=2+tz=3+2t.

Bài 5. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 2z + m = 0 và điểm A (1; 1; 1). Tính m để khoảng cách từ điểm A đến mặt phẳng (P) bằng 1?

Xem thêm phương pháp giải các dạng bài tập Toán lớp 12 hay, chi tiết khác:

• Bài toán Cực trị trong hình học không gian và cách giải
• Tọa độ điểm, tọa độ vectơ và cách giải
• Tích vô hướng và tích có hướng của hai vectơ và cách giải
• Các bài toán về phương trình mặt phẳng và cách giải
• Phương trình đường thẳng và cách giải bài tập

Săn SALE shopee Tết:

• Đồ dùng học tập giá rẻ
• Sữa dưỡng thể Vaseline chỉ hơn 40k/chai
• Tsubaki 199k/3 chai
• L'Oreal mua 1 tặng 3