Trong bài viết này, chúng ta sẽ cùng tìm hiểu về các khái niệm cơ bản về các loại số thường được sử dụng trong lập trình nhúng.
Mục tiêu
- Hiểu được số nhị phân (binary), số thập lục phân (hexadecimal), kiểu số nguyên có dấu và không dấu (signed và unsigned integers).
- Cách chuyển đổi giữa các kiểu số.
Giới thiệu
Chúng ta đã quá quen với hệ thập phân, gồm các số từ 0 đến 9. Hệ nhị phân tương tự nhưng chỉ có hai giá trị là 0 và 1. Còn hệ thập lục phân sử dụng các số từ 0 đến 9 và các chữ cái từ A đến F. Hãy xem qua một số ví dụ để hiểu thêm về cách chuyển đổi.
Hệ thập phân: 1984 = 1 10^3 + 9 10^2 + 8 10^1 + 4 10^0
Hệ nhị phân: 01101010 = 0 2^7 + 1 2^6 + 1 2^5 + 0 2^4 + 1 2^3 + 0 2^2 + 1 2^1 + 0 2^0 = 64 + 32 + 8 + 2 = 106
Hệ thập lục phân: 0x12AD = 1 16^3 + 2 16^2 + 10 16^1 + 13 16^0 = 4096 + 512 + 160 + 13 = 4781
Chuyển đổi giữa số nhị phân và thập phân
Hầu hết các số nhị phân được lưu trong bộ nhớ của máy tính sẽ có độ dài là 8, 16, hoặc 32 bit. 8-bit được gọi là 1 byte, 16-bit được gọi là halfword, và 32-bit được gọi là word.
Chuyển từ nhị phân sang thập phân
Ví dụ: Giá trị thập phân của số nhị phân 8 bit 11111111 là bao nhiêu?
11111111 = 1 2^7 + 1 2^6 + 1 2^5 + 1 2^4 + 1 2^3 + 1 2^2 + 1 2^1 + 1 2^0 = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
Ví dụ: Giá trị thập phân của số nhị phân 8 bit 01101010
01101010 = 0 2^7 + 1 2^6 + 1 2^5 + 0 2^4 + 1 2^3 + 0 2^2 + 1 2^1 + 0 2^0 = 64 + 32 + 8 + 2 = 106
Chuyển từ thập phân sang nhị phân
Ví dụ: Giá trị nhị phân của số thập phân 123 là bao nhiêu?
123/2 = 61 dư 1 61/2 = 30 dư 1 30/2 = 15 dư 0 15/2 = 7 dư 1 7/2 = 3 dư 1 3/2 = 1 dư 1 1/2 = 0 dư 1
Giá trị số nhị phân là 1111011
Ví dụ: Giá trị nhị phân của số thập phân 254
254/2 = 127 dư 0 127/2 = 63 dư 1 63/2 = 31 dư 1 31/2 = 15 dư 1 15/2 = 7 dư 1 7/2 = 3 dư 1 3/2 = 1 dư 1 1/2 = 0 dư 1
Giá trị số nhị phân là 11111110
Chuyển đổi giữa số nhị phân và thập lục phân
Số nhị phân là ngôn ngữ mặc định của máy tính, nhưng lại gây quá nhiều bối rối cho chúng ta. Để đơn giản hóa công việc với các số nhị phân, chúng ta sử dụng số thập lục phân (hexadecimal).
Với số thập lục phân, các giá trị có thể là các số từ 0 đến 9 và các chữ cái từ A đến F. Trong các máy tính, không có sự phân biệt giữa chữ hoa và chữ thường trong số thập lục phân, nên các giá trị 0-9 và a-f được coi là giống nhau.
Chúng ta thường gọi số thập lục phân là số "hex" và để phân biệt với các số khác, thường có 0x hoặc $ ở phía trước số thập lục phân. Trong C, thường sử dụng 0x. Các số thập lục phân cơ bản là 16, 161, 162, 163, ... hoặc 1, 16, 256, 4096, ...
Nibble thường được dùng để định nghĩa 4 bit nhị phân hoặc 1 số thập lục phân (16 = 2^4). Mỗi nibble này tương ứng với 1 số hex như sau:
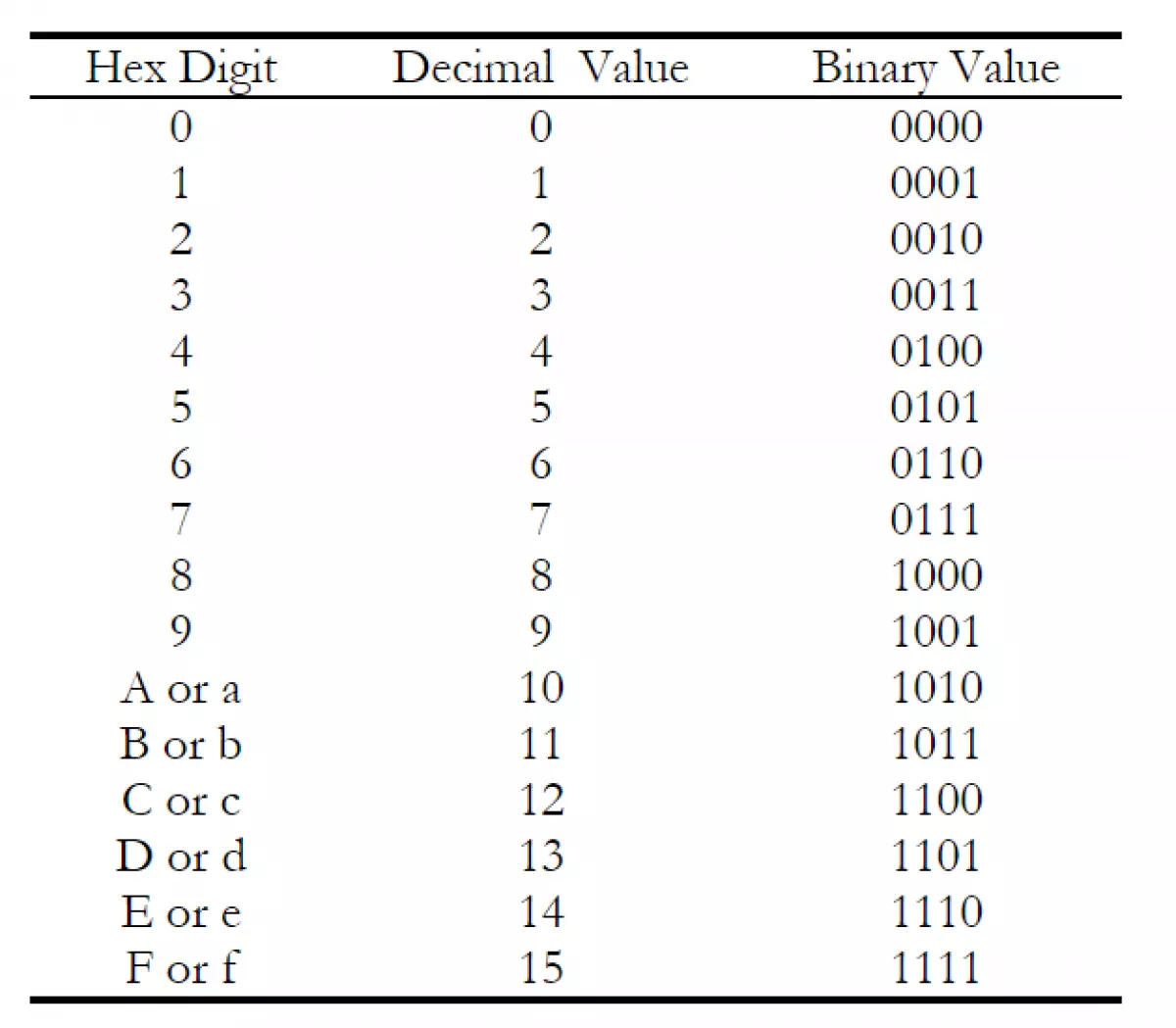
Để chuyển từ số nhị phân (binary) sang thập lục phân (hexadecimal) và ngược lại, chúng ta sẽ xem hình minh họa sau:
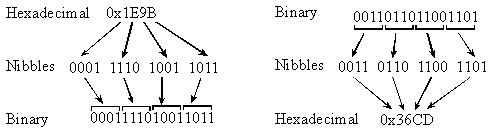
Chuyển từ thập lục phân sang nhị phân
Bước 1: Chuyển từng số trong số hex sang nibble.
Bước 2: Kết hợp các nibble lại thành số nhị phân.
Ví dụ: Chuyển số hex 0x40 về số nhị phân
Đầu tiên chia từng số hex ra và chuyển về số nhị phân 0x4 = 0100 và 0x0 = 0000. Sau đó kết hợp 2 số này lại thành 1 là 01000000. Vậy 0x40 = 01000000.
Ví dụ: Chuyển số hex 0x63F về số nhị phân
Đầu tiên chia từng số hex ra và chuyển về số nhị phân 0x6 = 0110, 0x3 = 0011, 0xF = 1111. Sau đó kết hợp 3 số này lại thành 1 là 011000111111. Vậy 0x63F = 011000111111.
Chuyển từ nhị phân sang thập lục phân
Bước 1: Chia các số nhị phân thành các nibble hợp lý.
Bước 2: Chuyển các nibble này thành số hex tương ứng.
Ví dụ: Chuyển số nhị phân 01000101 về số hex
Đầu tiên chia số nhị phân thành nhóm 4 bit 0100 = 0x4 và 0101 = 0x5. Tiếp tục kết hợp 2 số này lại thành 1 là 0x45. Vậy 01000101 = 0x45.
Ví dụ: Chuyển số nhị phân 11001010 về số hex
Đầu tiên chia số nhị phân thành nhóm 4 bit 1100 = 0xC và 1010 = 0xA. Tiếp tục kết hợp 2 số này lại thành 1 là 0xCA. Vậy 11001010 = 0xCA.
Vậy giá trị thập phân của số thập lục phân 8 bit 0xFF là bao nhiêu?
0xFF = 15 16^1 + 15 16^0 = 255
Precision và Byte
Precision có ý nghĩa là số giá trị riêng biệt hoặc các giá trị khác biệt, được biểu thị dưới dạng alternative (số thay thế), byte, hoặc binary bit (bit nhị phân).
Ví dụ: Định dạng của một số 8-bit có thể biểu diễn được 256 số khác nhau. Cụ thể, với 8-bit của DAC (chuyển đổi số tương tự), có thể tạo ra 256 giá trị output analog hoặc với 8-bit ADC (chuyển đổi tương tự số), có thể đo được 256 giá trị khác nhau từ input analog.
Ta có thể xem bảng sau để biết mối quan hệ giữa precision trong bit nhị phân và trong alternative. Ký hiệu [[x]] được định nghĩa là giá trị integer lớn nhất. Cột byte là số byte mà bộ nhớ sử dụng để lưu trữ.
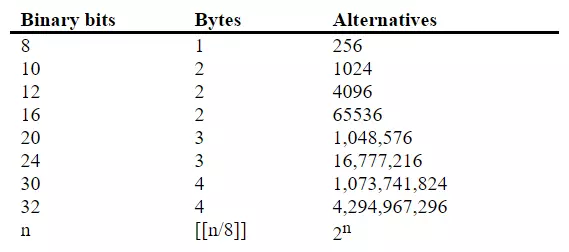
Một byte sẽ bao gồm 8-bit, với từng bit từ b7 đến b0 là các số nhị phân có giá trị là 1 hoặc 0. b7 thường được gọi là Most Significant Bit (MSB) hoặc bit có trọng số lớn nhất, và b0 là Least Significant Bit (LSB) hay bit có trọng số nhỏ nhất.
Nếu 1 byte được dùng để biểu diễn số unsigned, giá trị của số này sẽ được tính bằng công thức:
N = 128 b7 + 64 b6 + 32 b5 + 16 b4 + 8 b3 + 4 b2 + 2 * b1 + b0
Trọng số của bit n là 2^n và có tới 256 số unsigned 8-bit khác nhau. Số nhỏ nhất là 0 và số lớn nhất là 255.
Ví dụ: Số nhị phân 00001010 là 8 + 2 = 10
Ngoài ra, với LSB, ta có thể biết một số là số chẵn (even) hay lẻ (odd).
Ví dụ:

2's Complement
Trước khi bắt đầu, hãy nhớ rằng:
- Nếu bit nhị phân trọng số thấp là 0, thì số đó là số chẵn.
- Nếu bit ngoài cùng bên phải của n bit là 0, thì số đó chia hết cho 2^n.
- Với một số 8-bit unsigned, nếu bit 7 là low (0), thì số đó sẽ có giá trị từ 0 - 127, và bit 7 là high (1), thì số sẽ có giá trị từ 128 - 255.
Một trong những cách đầu tiên để biểu diễn số signed được gọi là one's complement. Với cách này, chúng ta sẽ đảo toàn bộ các bit của số unsigned để có được số âm.
Ví dụ: Nếu số 25 = 00011010, thì số -25 = 11100101. Do đó, một số 8-bit one's complement sẽ có giá trị từ -127 tới +127. Bit đầu tiên sẽ là bit sign (bit có dấu) bằng 1 nếu đó là số âm. Tuy nhiên, vấn đề ở đây là một số one's complement không có dạng cơ bản. Vì vậy, two's complement ra đời để khắc phục điều này.
Với two's complement, cách thực hiện là giống với one's complement, nhưng chúng ta sẽ cộng thêm 1.
Ví dụ: Nếu số 25 = 00011010, thì -25 = 11100110.
Vậy giá trị của một số signed 8-bit two's complement là:
N = -128 b7 + 64 b6 + 32 b5 + 16 b4 + 8 b3 + 4 b2 + 2 * b1 + b0
Ta có thể xác định các thành phần cơ bản của số 8-bit signed là {-128, 64, 32, 16, 8, 4, 2, 1}.
Chúng ta tiếp tục qua một số ví dụ nữa:
Ví dụ: Giá trị của số 11100111 dưới dạng signed và unsigned integer
Giá trị Unsigned = 1 2^7 + 1 2^6 + 1 2^5 + 0 2^4 + 0 2^3 + 1 2^2 + 1 2^1 + 1 2^0 = 231 Giá trị Signed = -1 2^7 + 1 2^6 + 1 2^5 + 0 2^4 + 0 2^3 + 1 2^2 + 1 2^1 + 1 2^0 = -25
Chuyển đổi số 45 decimal về 8-bit binary và hexadecimal
45 = 32 + 8 + 4 + 1, nên 45 = 00101101 = 0x2D.
Chuyển đổi số 200 decimal về 8-bit binary và hexadecimal
200 = 128 + 64 + 8, nên 200 = 11001000 = 0xC8.
Chuyển số signed 11011010 về decimal.
-128 + 64 + 16 + 8 + 2 = -38.
Giá trị của số signed và unsigned là khác nhau do MSB. Do đó, máy tính không thể xác định được đó là số signed hay unsigned, do đó người lập trình phải biết được điều này bằng cách sử dụng biến dữ liệu 32-bit kiểu long.
Words và Halfwords
Một halfword hoặc double byte gồm 16 bit, với mỗi bit b15,...,b0 là số nhị phân có giá trị 0 hoặc 1.
Nếu halfword được sử dụng để biểu thị số unsigned, thì giá trị của nó sẽ là:
N = 32768 b15 + 16384 b14 + 8192 b13 + 4096 b12+ 2048 b11 + 1024 b10 + 512 b9 + 256 b8+ 128 b7 + 64 b6 + 32 b5 + 16 b4 + 8 b3 + 4 b2 + 2 * b1 + b0
Có 65536 giá trị khác nhau của số 16-bit unsigned. Số nhỏ nhất là 0 và lớn nhất là 65535. Các thành phần cơ bản là {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768}.
Ví dụ: Giá trị của 0010000110000100 hoặc 0x2184 là 8192 + 256 + 128 + 4 = 8580.
Một word trong ARM Cortex-M sẽ gồm 32 bit. Giống như số unsigned với 32 bit, mỗi bit b31,...,b0 sẽ là số nhị phân và có giá trị 1 hoặc 0.
Nếu số 32-bit được dùng để biểu diễn số unsigned integer, thì giá trị của số này là:
N = 231 b31 + 230 b30 + ... + 2 b1 + b0 = sum(2^i bi) for i=0 to 31
Có 232 số unsigned 32-bit khác nhau. Số nhỏ nhất là 0 và lớn nhất là 232-1. Các thành phần cơ bản là {1, 2, 4, ..., 229, 230, 231}.
Nếu số 32-bit được dùng để biểu diễn số signed, thì giá trị của nó là:
N = -231 b31 + 230 b30 + ... + 2 b1 + b0 = -231 b31 + sum(2^i * bi) for i=0 to 30
Và các thành phần cơ bản {1, 2, 4, ..., 229, 230, -231}
Tạm Kết
Chúng ta đã tìm hiểu về các khái niệm và ví dụ minh họa về các hệ số và các cách chuyển đổi giữa các số nhị phân, thập phân, thập lục phân, các khái niệm về precision và byte, 2's Complement với signed và unsigned, word và halfword.












