Tam giác vuông là một trong những chủ đề quan trọng trong toán học. Việc hiểu và áp dụng đúng hệ thức về góc và cạnh trong tam giác vuông không chỉ giúp các em học sinh ôn tập mà còn giúp các em xây dựng nền tảng vững chắc cho các chủ đề toán cao cấp hơn. Trong bài viết này, chúng ta sẽ tìm hiểu cách giải bài tập về hệ thức về góc và cạnh trong tam giác vuông lớp 9.
Lý thuyết và Phương pháp giải
1. Các hệ thức
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề
b) Cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề
Chuyên đề Toán lớp 9
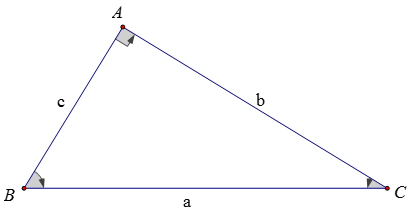
Ví dụ: b = a.sinB = a.cosC, c = a.sinC = a.cosB, b = c.tanB = c.cotC, c = b.tanB = b.cotC
2. Giải tam giác vuông
Là tìm tất cả các yếu tố còn lại của một tam giác vuông khi biết trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông)
Ví dụ minh họa
Ví dụ 1: Giải tam giác ABC vuông tại A biết AC = 4,1 cm; BC = 5,7 cm
Lời giải:
Xét tam giác ABC vuông tại A:
Áp dụng định lí Pytago có:
BC^2 = AB^2 + AC^2
Chuyên đề Toán lớp 9
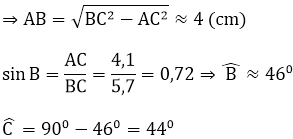
Ví dụ 2: Cho tam giác ABC nhọn, Vẽ 3 đường cao AD, BE, CF. Chứng minh rằng:
AE BF CD = AB BC CA cosA cosB * cosC
Chuyên đề Toán lớp 9
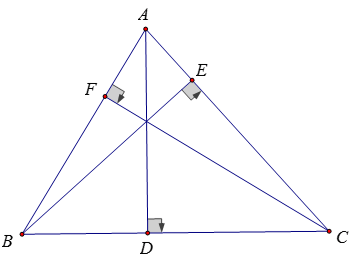
Lời giải:
Đặt ΔABE vuông tại E có: AE = AB * cosA
Đặt ΔFBC vuông tại F có: BF = BC * cosB
Đặt ΔADC vuông tại D có: CD = AC * cosC
⇒ AE BF CD = AB BC CA cosA cosB * cosC
Ví dụ 3: Cho tam giác nhọn ABC, AB < AC, đường cao AH = h và đường trung tuyến AM, đặt góc HAM bằng α. Chứng minh rằng:
a) HC - HB = 2h * tanα
Lời giải:
Chuyên đề Toán lớp 9
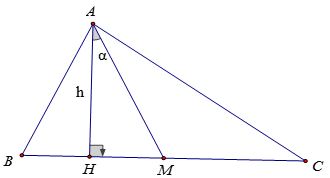
a) Ta có:
HC - HB = HM + MC - (MB - HM)
= HM + MC - MB + HM = 2HM (Do MB = MC)
= 2AH tanα = 2h tanα
b) Δ AHC vuông tại H có: HC = AH cotC = h cotC
Δ AHB vuông tại H có: HB = AH cotB = h cotB
Do đó: HC - HB = h(cotC - cotB)
⇒ 2h * tanα = h(cotC - cotB)
Ví dụ 4: Tam giác ABC có diện tích S, các đường cao không nhỏ hơn 1 cm. Chứng minh rằng S ≥ √3/3 cm^2
Lời giải:
Chuyên đề Toán lớp 9
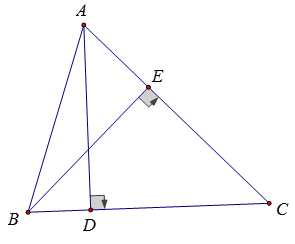
Giả sử:
SinC ≤ √3/2
Vẽ các đường cao AD và BE
Xét tam giác EBC vuông tại E có: BE = BC * sinC
Diện tích tam giác ABC là:
Vậy S ≥ √3/3 cm^2 (dấu bằng xảy ra khi ΔABC đều)
Ví dụ 5: Cho hình bình hành ABCD, góc D bằng α < 90°. Vẽ BH ⊥ CD; BK ⊥ AD.
a) Chứng minh rằng ΔBHK ~ ΔABD
b) Chứng minh rằng HK = BD * sinα
c) Tính diện tích tứ giác KBHD biết AB = 6cm; AD = 4cm; α = 60°
Lời giải:
Chuyên đề Toán lớp 9
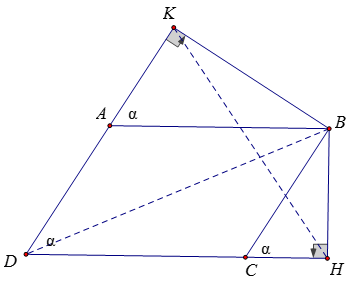
Xét tam giác ABK và tam giác CBH có:
Chuyên đề Toán lớp 9
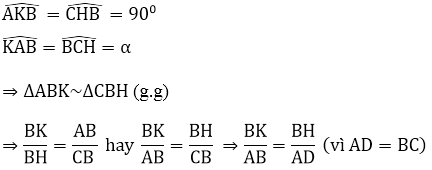
Xét ΔBHK và ΔADB có:
Chuyên đề Toán lớp 9
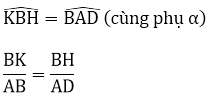
⇒ ΔBHK ~ ΔADB (c.g.c)
b) ΔBHK ~ ΔADB
Xét ΔBCH vuông tại H có: BH = BC * sinα
c) Xét ΔKAB vuông tại K có: AK = AB cosα = 6 cos 60° = 3(cm) ⇒ DK = 7cm, BK = AB sinα = 6 sin 60° =3√3 (cm)
Xét ΔHBC vuông tại H có: CH = BC cosα = 4 cos 60° = 2(cm) ⇒ DH = 8cm
Diện tích tứ giác KBHD là:
Chuyên đề Toán lớp 9
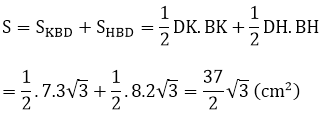
Đây chỉ là một số ví dụ đơn giản về cách giải bài tập về hệ thức về góc và cạnh trong tam giác vuông lớp 9. Hy vọng qua bài viết này, các em đã hiểu được cách áp dụng các hệ thức này để giải quyết các bài toán thực tế. Hãy ôn tập và luyện tập thường xuyên để nắm vững kiến thức này nhé!
Săn SALE shopee Tết:
-
Đồ dùng học tập giá rẻ
-
Sữa dưỡng thể Vaseline chỉ hơn 40k/chai
-
Tsubaki 199k/3 chai
-
L'Oreal mua 1 tặng 3
-
Hơn 20.000 câu trắc nghiệm Toán, Văn, Anh lớp 9 có đáp án
