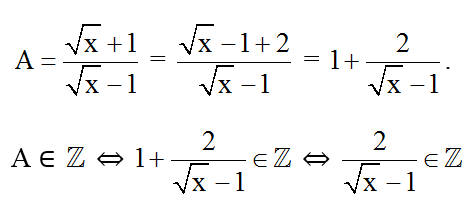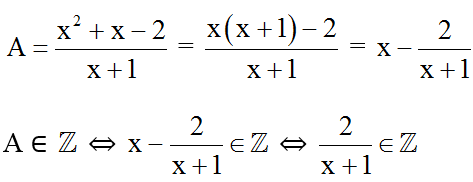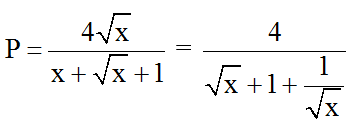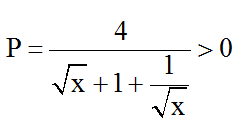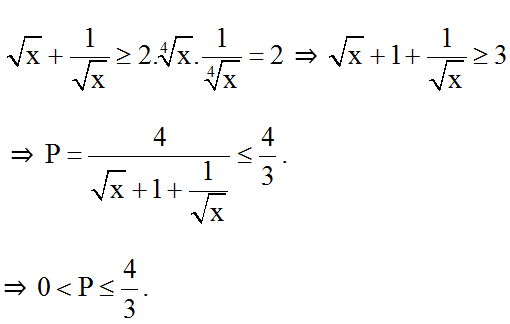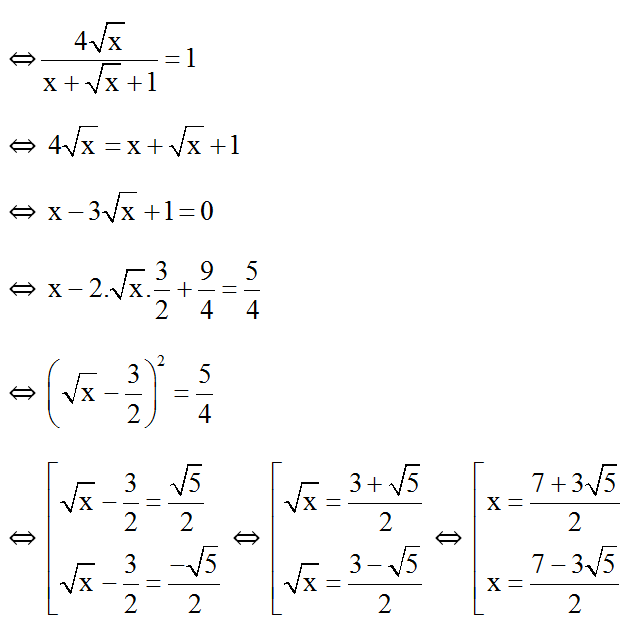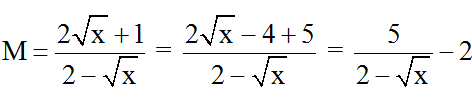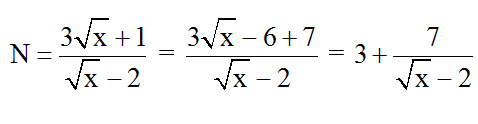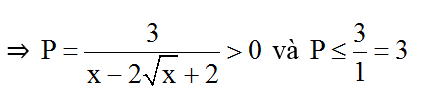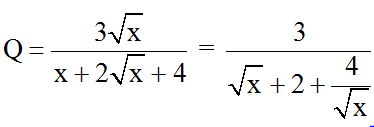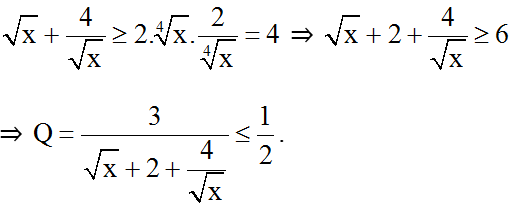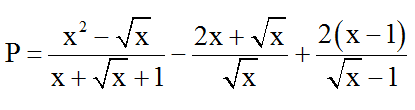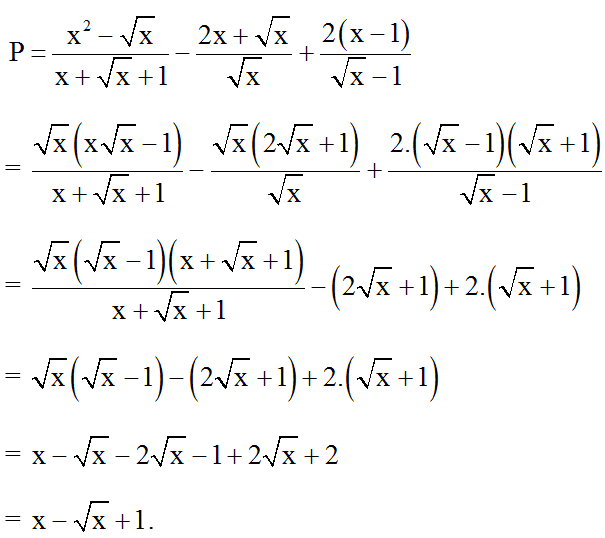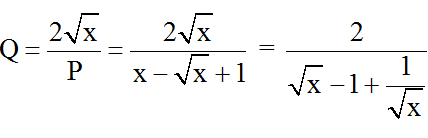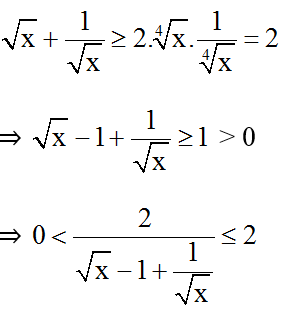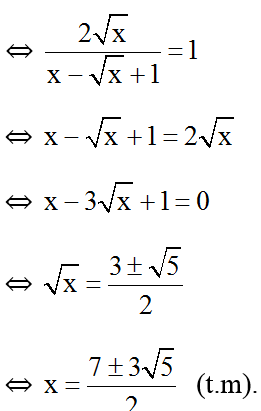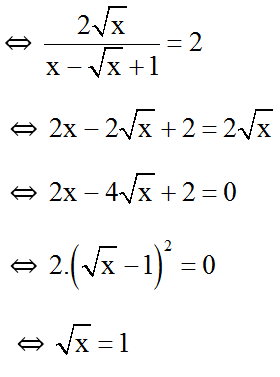Bài tập Tìm giá trị của biến để biểu thức có giá trị nguyên cực kỳ quan trọng trong việc ôn tập và nắm vững kiến thức cho học sinh. Với phương pháp giải chi tiết và đa dạng bài tập, học sinh sẽ nắm vững cách làm và áp dụng vào các bài tập tương tự.
Dạng bài tập Tìm giá trị của biến để biểu thức có giá trị nguyên cực hay
Phương pháp giải
a) Tìm x nguyên để biểu thức A = nguyên.
Bước 1. Tách A thành dạng trong đó h(x) là một biểu thức nguyên khi x nguyên, m là nguyên.
Bước 2: A nguyên ⇔ g(x) ∈ Ư(m).
Bước 3. Với mỗi giá trị của g(x), tìm x tương ứng và kết luận.
b) Tìm x để biểu thức A nguyên (Sử dụng phương pháp kẹp).
Bước 1: Áp dụng các bất đẳng thức để tìm hai số m, M sao cho m < A < M.
Bước 2: Tìm các giá trị nguyên trong khoảng từ m đến M.
Với mỗi trường hợp, tìm giá trị của x và kết luận.
Lưu ý: Đối chiếu điều kiện xác định của biểu thức.
Ví dụ minh họa
Ví dụ 1: Với giá trị nguyên nào của x thì biểu thức cũng đạt giá trị nguyên?
Hướng dẫn giải:
Điều kiện xác định: x ≥ 0; x ≠ 1 .
Ta có:
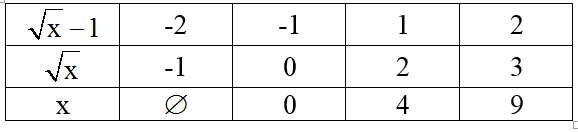
⇔ √x - 1 ∈ Ư(2) = {-2; -1; 1; 2}
Ta có bảng sau:
Vậy với x ∈ {0; 4; 9} thì biểu thức A đạt giá trị nguyên.
Ví dụ 2: Tìm giá trị nguyên của x để biểu thức nguyên.
Hướng dẫn giải:
Đkxđ: x ≠ -1.
Ta có:
⇔ x + 1 ∈ Ư(2) = {-2; -1; 1; 2}
⇔ x ∈ {-3; -2; 0; 1}.
Vậy với x ∈ {-3; -2; 0; 1} thì biểu thức A nguyên.
Ví dụ 3: Tìm x để biểu thức đạt giá trị nguyên.
Hướng dẫn giải:
Đkxđ: x ≥ 0.
Ta có:
Ta có: với mọi x
⇒
Áp dụng bất đẳng thức Cô-si ta có:
P đạt giá trị nguyên ⇔ P = 1
Vậy với thì biểu thức P đạt giá trị nguyên.
Bài tập trắc nghiệm tự luyện
Bài 1: Giá trị nào của x dưới đây không làm cho biểu thức nguyên.
A. 1/4 B. 4 C. 2 D. 0.
Bài 2: Có bao nhiêu giá trị nguyên của x để biểu thức nguyên?
A. 3 B. 4 C. 6 D. 8
Bài 3: Có tất cả bao nhiêu giá trị nguyên của x để biểu thức nguyên?
A. 2 B. 3 C. 4 D. 5
Bài 4: Với tất cả các số nguyên x, giá trị nguyên lớn nhất của biểu thức là:
A. 1 B. 2 C. 3 D. 4
Bài 5: Có bao nhiêu giá trị của x để biểu thức nguyên?
A. 2 B. Vô số C. 3 D. 1
Bài 6: Tìm các giá trị nguyên của x để các biểu thức dưới đây nguyên:
Hướng dẫn giải:
a) Đkxđ: x ≠ -3.
A ∈ Z ⇔ ⇔ x + 3 ∈ Ư(3) = {-3; -1; 1; 3} ⇔ x ∈ {-6; -4; -2; 0}
b) Đkxđ: x ≠ 1/3 .
B ∈ Z ⇔ ⇔ 1 - 3x ∈ Ư(6) = {-6; -3;-2; -1; 1; 2; 3; 6}
Ta có bảng:
Trong các giá trị trên, chỉ có x = 1 hoặc x = 0 thỏa mãn x nguyên.
Vậy x = 0 hoặc x = 1.
c) ⇔ 2 - 3√x ∈ Ư(2) = {-2; -1; 1; 2}
Ta có bảng sau:
Trong các giá trị trên chỉ có x = 1 hoặc x = 0 thỏa mãn.
Vậy x = 0 hoặc x = 1.
Bài 7: Tìm các giá trị nguyên của x để các biểu thức dưới đây nguyên:
Hướng dẫn giải:
a)
Đkxđ: x ≥ 0; x ≠ 4 .
Ta có:
.
M ∈ Z ⇔ ∈ Z ⇔ 2 - √x ∈ Ư(5) = {-5; -1; 1; 5}.
Ta có bảng:
Vậy với x ∈ {49; 9; 1} thì biểu thức M có giá trị nguyên.
b)
Đkxđ: x ≥ 0 ; x ≠ 4 .
Ta có:
N ∈ Z ⇔ ⇔ √x - 2 Ư(7) = {-7; -1; 1; 7}
Ta có bảng sau:
Trong các giá trị trên chỉ có x = 1 hoặc x = 0 thỏa mãn.
Vậy x = 0 hoặc x = 1.
Bài 8: Tìm các giá trị của x để các biểu thức nguyên
Hướng dẫn giải:
Điều kiện: x ≥ 0 .
Ta có: x - 2√x + 2 = x - 2√x + 1 + 1 = (√x - 1)2 + 1 ≥ 1 > 0
⇒ 0 < P ≤ 3 .
P nguyên ⇔ P ∈ {1; 2; 3}.
-
P = 1 ⇔ x - 2√x + 2 = 1 ⇔ x - 2√x + 1 = 0 ⇔ √x - 1 = 0 ⇔ x = 1.
-
P = 2 ⇔ x - 2√x + 2 = 1/4 ⇔ (√x - 1)2 = -3/4 < 0. Vô nghiệm.
-
P = 3 ⇔ x - 2√x + 2 = 1/9 ⇔ (√x - 1)2 = -8/9 < 0. Vô nghiệm.
Vậy chỉ có x = 1 làm cho P nguyên.
Bài 9: Chứng minh rằng biểu thức không nguyên với mọi giá trị của x làm cho biểu thức xác định.
Hướng dẫn giải:
Ta có:
Áp dụng bất đẳng thức Cô-si ta có:
Mà Q > 0 với mọi x.
⇒ 0 < Q ≤ 1/2
Vậy không có giá trị nào của x làm cho Q nguyên.
Bài 10: Cho
a) Rút gọn biểu thức P.
b) Tìm x để biểu thức nguyên.
Hướng dẫn giải:
a) Điều kiện xác định: x > 0; x ≠ 1.
b) Ta có:
Áp dụng bất đẳng thức Cô-si ta có:
⇒ hay 0 < Q ≤ 2 .
Q nguyên ⇔ Q = 1 hoặc Q = 2.
-
Q = 1
-
Q = 2
⇔ x = 1 (không t.m đkxđ).
Vậy với thì biểu thức Q có giá trị nguyên.
Xem thêm các dạng bài tập Toán lớp 9 có đáp án và lời giải chi tiết khác: link
Mục lục các Chuyên đề Toán lớp 9:
- Chuyên đề Đại Số 9
- Chuyên đề: Căn bậc hai
- Chuyên đề: Hàm số bậc nhất
- Chuyên đề: Hệ hai phương trình bậc nhất hai ẩn
- Chuyên đề: Phương trình bậc hai một ẩn số
- Chuyên đề Hình Học 9
- Chuyên đề: Hệ thức lượng trong tam giác vuông
- Chuyên đề: Đường tròn
- Chuyên đề: Góc với đường tròn
- Chuyên đề: Hình Trụ - Hình Nón - Hình Cầu
Săn SALE shopee Tết:
-
Đồ dùng học tập giá rẻ
-
Sữa dưỡng thể Vaseline chỉ hơn 40k/chai
-
Tsubaki 199k/3 chai
-
L'Oreal mua 1 tặng 3
-
Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 9 có đáp án