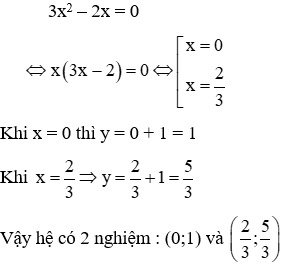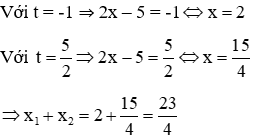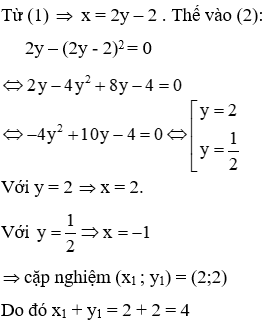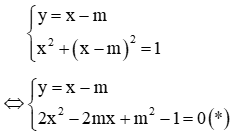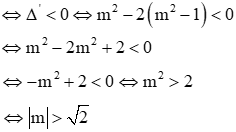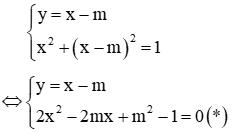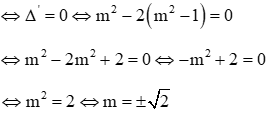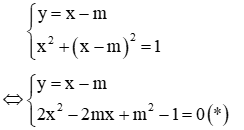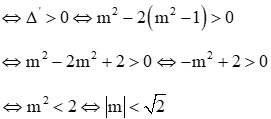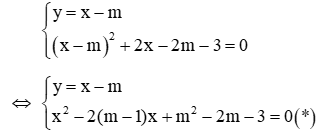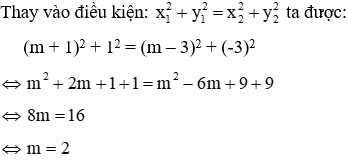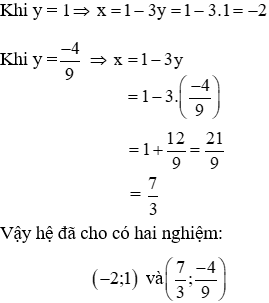Hệ phương trình 2 ẩn bậc hai có thể làm đau đầu nhiều học sinh. Tuy nhiên, không nên lo lắng! Bài viết này sẽ giúp bạn hiểu rõ cách giải hệ phương trình này một cách đơn giản và chi tiết.
Phương pháp giải
Để giải hệ phương trình chứa 2 ẩn x và y, gồm một phương trình bậc nhất và một phương trình bậc hai, chúng ta có thể rút x hoặc y từ phương trình bậc nhất và thế vào phương trình bậc hai.
Ví dụ 1: Giải hệ phương trình:
x + y = 3 (1) 2x^2 - 3y = 5 (2)Giải Từ phương trình (1) ⇒ y = 3 - x (*). Thế vào phương trình (2) ta được: 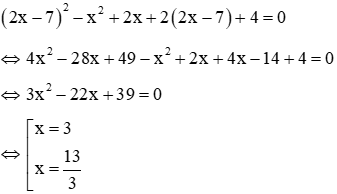
Ví dụ 2: Giải hệ phương trình:
2x + y = 5 (1) x^2 + y = 3 (2)Giải Từ phương trình (2) ⇒ y = 3 - x (*). Thế vào phương trình (1) ta được: 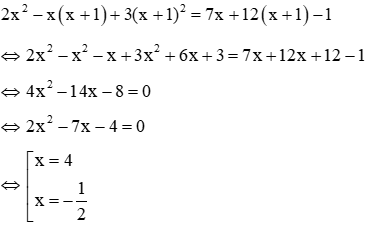
Ví dụ 3: Cho hệ phương trình:
2x + y = 3 (1) x^2 - mx + 2 = 0 (2)a. Giải hệ với m = 3 b. Tìm m để hệ có nghiệm duy nhất
Giải Từ phương trình (1) ⇒ y = 3 - 2x. Thế vào phương trình (2) ta được: a. Với m = 3 thì phương trình (*) trở thành: 3x^2 - 2x = 0
b. Hệ có nghiệm duy nhất khi () có nghiệm duy nhất. Ta có: TH1: Nếu m = 0 thì phương trình (): 4x - 3 = 0 (thỏa mãn) TH2: Nếu m ≠ 0 thì () là phương trình bậc 2. Khi đó () có nghiệm duy nhất khi:
Vậy với m = 0 hoặc m = 4 thì hệ có nghiệm duy nhất.
Bài tập
Câu 1: Cho hệ phương trình:
x + 2y = 0 (1) 2x^2 + x + 2y = 0 (2)Rút y từ phương trình (1) thế vào phương trình (2) ta được phương trình nào sau đây? A. x + 3 = 0 B. 2x^2 + x + 3 = 0 C. -x + 3 = 0 D. -x^2 + x + 3 = 0
Giải Từ (1)⇒ y = -x/2. Thế vào (2):
2x^2 - 3x - 5 = 0 ⇔ x^2 + x - x^2 + 3 = 0 ⇔ x + 3 = 0Vậy đáp án đúng là A
Câu 2: Cho hệ phương trình:
x + y = -5 (1) 2(x + y)^2 - 3(x + y) - 5 = 0 (2)Biết rằng hệ đã cho có 2 nghiệm (x1 ; y1) và (x2 ; y2), tính x1 + x2
Giải Từ (1) ⇒ y = -x - 5. Thế vào (2): 2(x + (-x - 5))^2 - 3(x + (-x - 5)) - 5 = 0 ⇔ 2(-6)^2 - 3(-6) - 5 = 0 ⇔ 2(36) + 18 - 5 = 0
Đặt t = -6. Phương trình trở thành: 2t^2 - 3t - 5 = 0
Vậy đáp án đúng là C
Câu 3: Cho hệ phương trình:
x + y = 1 (1) x^2 + y = 4 (2)Biết rằng hệ đã cho có 2 nghiệm (x1 ; y1) và (x2 ; y2) trong đó x1 > x2, tính x1 + y1 A. 1 B. 2 C. 3 D. 4
Giải
Vậy đáp án đúng là D
Câu 4: Cho hệ phương trình:
x + y = 2 (1) (x - 2)^2 + (y + 4) = 0 (2)Rút x từ phương trình (1) thế vào phương trình (2) ta được phương trình nào sau đây? A. 2x^2 + 4 = 0 B. x^2 - 10x - 2 = 0 C. -x^2 - 4 = 0 D. x^2 - 5x + 4 = 0
Giải Từ (1) x = 2 - y. Thế vào (2): (2 - y - 2)^2 + (y + 4) = 0 ⇔ (-y)^2 + 4y - 4 + y + 4 = 0 ⇔ y^2 - 4y + 4 = 0 ⇔ (y - 2)^2 = 0 ⇔ y - 2 = 0 ⇔ y = 2
Vậy đáp án đúng là C
Câu 5: Cho hệ phương trình:
x + y = 1 (1) (x - 3)^2 + (y - 1)^2 + m = 0 (2)Giá trị của m để hệ vô nghiệm là:
Giải Biến đổi hệ đã cho về dạng:
Hệ vô nghiệm khi phương trình (*) vô nghiệm
Vậy đáp án đúng là B
Câu 6: Cho hệ phương trình:
x + y = 1 (1) (m - 2)x + y = 3 (2)Giá trị của m để hệ có nghiệm duy nhất là:
Giải Biến đổi hệ đã cho về dạng:
Hệ có nghiệm duy nhất khi phương trình (*) có nghiệm duy nhất
Vậy đáp án đúng là A
Câu 7: Cho hệ phương trình:
2x + y = 4 (1) 3x^2 - 4x + y = 4 (2)Giá trị của m để hệ có hai nghiệm là:
Giải Biến đổi hệ đã cho về dạng:
Hệ có 2 nghiệm khi phương trình (*) có 2 nghiệm
Vậy đáp án đúng là C
Câu 8: Cho hệ phương trình:
2x + y = 4 (1) (x + 1)(x - 3) + y = m (2)Tìm m để hệ có hai nghiệm (x1 ; y1) và (x2 ; y2) sao cho x1 + y1 = x2 + y2
Giải Biến đổi hệ đã cho về dạng:
Hệ có 2 nghiệm khi phương trình () có 2 nghiệm ⇔ Δ' > 0 ⇔ (m - 1)^2 - m^2 + 2m + 3 > 0 ⇔ 4 > 0 (∀ m) ⇒ phương trình () luôn có 2 nghiệm : x1 = m + 1; x2 = m - 3 Với x1 = m + 1 ⇒ y1 = 1 Với x2 = m - 3 ⇒ y2 = -3
Vậy đáp án đúng là B
Câu 9: Cho hệ phương trình:
x + 2y = 0 (1) 2x^2 + 4x - 3y = 0 (2)Rút y từ phương trình (1) thế vào phương trình (2) ta được phương trình nào sau đây? A. 2x^2 + 4x - 3 = 0 B. x^2 - 10x - 2 = 0 C. 3x^2 - 4x + 4 = 0 D. x^2 - 5x + 1 = 0
Giải Từ (1)⇒ y = -x/2. Thế vào (2):
2x^2 + 4x - 3(-x/2) = 0 ⇔ 2x^2 + 4x + 3x/2 = 0Vậy đáp án đúng là B
Câu 10: Số nghiệm của hệ phương trình là A. 1 B. 2 C. 3 D. 4
Giải Từ (1)⇒ x = 1 - y. Thế vào (2): (1 - y)^2 + y - 5 = 0 ⇔ 9y^2 - 6y + 1 + y - 5 = 0 ⇔ 9y^2 - 5y - 4 = 0 Phương trình 9y^2 - 5y - 4 = 0 có a + b + c = 9 - 5 - 4 = 0 nên có 2 nghiệm y = 1, y = -4
Vậy đáp án đúng là B