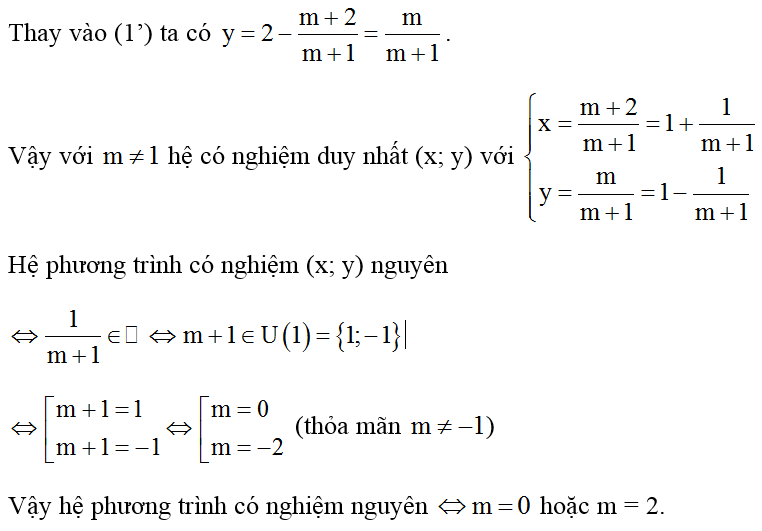Hệ phương trình là một chủ đề quan trọng trong môn Toán lớp 9. Việc giải hệ phương trình cần sự tỉ mỉ và khéo léo để tìm ra các giá trị nghiệm thích hợp. Trong bài viết này, chúng ta sẽ tìm hiểu về cách giải hệ phương trình và sẽ có một số bài tập để ôn tập và nắm vững kiến thức.
Giải hệ phương trình Toán lớp 9
A. Phương pháp giải
- Bước 1: Từ một phương trình của hệ phương trình đã cho, ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại để được một phương trình mới (chỉ còn một ẩn).
- Bước 2: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ phương trình đã cho.
Chú ý:
- Để có lời giải đơn giản, ta thường chọn các phương trình có hệ số không quá lớn (bằng 1 hoặc -1) và biểu diễn ẩn có hệ số nhỏ hơn qua ẩn còn lại.
- Thay một phương trình trong hệ bởi phương trình một ẩn vừa tìm ta được hệ phương trình mới tương đương với hệ phương trình đã cho.
B. Bài tập tự luận
Bài 1: Giải các hệ phương trình sau bằng phương pháp thế:
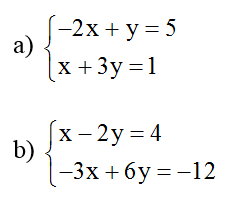
Hướng dẫn giải Thế (1) vào (2) ta được: x + 3(2x + 5) = 1 ⇔ x + 6x + 15 = 1 ⇔ 7x = -14 ⇔ x = -2 Thay x = -2 vào (1) ta được y = 2.(-2) + 5 = 1 Vậy hệ phương trình có nghiệm duy nhất (-2;1)
Thế (1) vào (2) ta được: -3(2y + 4) + 6y = -12 ⇔ -6y -12 + 6y = -12 ⇔ 0y = 0 (luôn đúng) Vậy hệ phương trình có vô số nghiệm (x;y) thỏa mãn x = 2y +4 và y ∈ R.
Bài 2: Cho hàm số y = ax + b. Xác định a, b để đồ thị hàm số đi qua hai điểm M(-1; 2) và N(√3;-7).
Hướng dẫn giải Do hàm số y = ax + b có đồ thị đi qua M(-1; 2) nên thay x = -1 và y = 2 vào phương trình ta có: 2 = -a + b (1) Tương tự, hàm số y = ax + b đi qua N(√3;-7) nên ta có: -7 = √3a + b (2)

Bài 3: Trong mặt phẳng Oxy, viết phương trình đường thẳng AB trong các trường hợp: a) A(-1; 1) và B(2; 4) b) A(0; -1) và B(1; 0)
Hướng dẫn giải a) Gọi phương trình đường thẳng cần tìm là y=ax+b Vì đường thẳng đi qua A(-1; 1) nên ta có: 1=-a+b (1) Vì đường thẳng đi qua B(2;4) nên ta có: 4=2a+b (2) Từ (1) và (2) => a = 3 và b = 4 Vậy phương trình đường thẳng cần tìm là y = 3x + 4.
b) Gọi phương trình đường thẳng cần tìm là y = ax + b Vì đường thẳng đi qua A(0;-1) nên ta có: -1 = 0.a + b ⇔ b = -1. Vì đường thẳng đi qua B(1;0) nên ta có: 0 = a + b (1) Thay b = -1 vào (1) ta được a = 1 Vậy đường thẳng cần tìm là y = x - 1.
Bài 4: a) Giải hệ phương trình với m = -2. b) Tìm m để hệ phương trình có nghiệm nguyên.
Hướng dẫn giải

Săn SALE shopee Tết:
- Đồ dùng học tập giá rẻ
- Sữa dưỡng thể Vaseline chỉ hơn 40k/chai
- Tsubaki 199k/3 chai
- L'Oreal mua 1 tặng 3
Những bài tập trên là một số ví dụ về việc giải hệ phương trình lớp 9. Hy vọng qua bài viết này, bạn đã nắm vững cách giải và có thể áp dụng vào việc ôn tập và giải các bài tập khó hơn. Chúc bạn có một hành trình học tập vui vẻ và thành công!