Phương trình bậc 2 là một trong những dạng phương trình thường gặp trong quá trình học, làm bài tập và trong các bài thi THCS. Để giải phương trình này, không ít học sinh đã gặp khó khăn. Trong bài viết này, chúng ta sẽ tìm hiểu cách giải phương trình bậc 2 để nắm bắt kiến thức tổng quát về dạng phương trình này.
A. Phương trình bậc 2 là gì
Phương trình bậc 2 là phương trình tổng quát có dạng: ax² + bx + c = 0 (với điều kiện: a≠0). Việc giải phương trình bậc 2 là tìm tất cả các giá trị của x để thỏa mãn phương trình này.
Để hiểu thêm về phương trình bậc 2, bạn có thể tham khảo bài viết Phương trình bậc 2 một ẩn.
B. Phương pháp giải phương trình bậc 2
Để giải phương trình bậc 2, ta cần thực hiện theo các bước sau:
Bước 1: Tính giá trị của Δ (delta) với Δ = b² - 4ac
Bước 2: Xét tập nghiệm của phương trình bằng cách so sánh Δ với 0
- Δ < 0: phương trình bậc 2 vô nghiệm
- Δ = 0: phương trình bậc 2 có nghiệm kép (x1 = x2 = -b/2a)
- Δ > 0: phương trình bậc 2 có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau:
Lưu ý: Trong một số trường hợp đặc biệt, bạn có thể nhẩm nhanh nghiệm của phương trình bậc 2.
- Trong trường hợp a + b + c = 0 thì x1 = 1, x2 = c/a
- Trong trường hợp a - b + c = 0 thì x1 = -1, x2 = -c/aĐể biết thêm về công thức nghiệm của phương trình bậc 2, bạn có thể tham khảo bài viết Công thức nghiệm của phương trình bậc 2.
Một số ví dụ giải phương trình bậc 2
Ví dụ 1: Giải phương trình 4x² - 2x - 6 = 0 Ta có: Δ = (-2)² - 4.4.(-6) = 4 + 96 = 100 > 0 => Vậy phương trình 4x² - 2x - 6 = 0 có 2 nghiệm phân biệt. Áp dụng công thức ta có:
x1 = (-(-2) + √100) / (2.4) = 3/2
x2 = (-(-2) - √100) / (2.4) = -1/2Ví dụ 2: Giải phương trình 2x² - 7x + 3 = 0 Ta có Δ = (-7)² - 4.2.3 = 49 - 24 = 25 > 0 => Vậy phương trình 2x² - 7x + 3 = 0 có 2 nghiệm phân biệt. Áp dụng công thức ta có:
x1 = (7 + √25) / (2.2) = 3
x2 = (7 - √25) / (2.2) = 1/2Ví dụ 3: Giải phương trình 3x² + 2x + 5 = 0 Ta có Δ = 2² - 4.3.5 = -56 < 0 => Vậy phương trình 3x² + 2x + 5 = 0 là phương trình vô nghiệm.
Ví dụ 4: Giải phương trình x² - 4x + 4 = 0 Ta có Δ = (-4)² - 4.4.1 = 0 => Vậy phương trình x² - 4x + 4 = 0 có nghiệm kép (hoặc còn gọi là phương trình có 2 nghiệm giống nhau). Bên cạnh đó, trong câu hỏi này, bạn có thể áp dụng hằng đẳng thức đáng nhớ: (a - b)² = a² - 2ab + b² nên phương trình trên về dạng (a - 2)² = 0 => x = 2.
C. Một số dạng bài về giải phương trình bậc 2
Dạng 1: Bài tập giải phương trình bậc 2 không chứa tham số
Để giải được phương trình thuộc dạng này, phương pháp phổ biến nhất là sử dụng công thức tính Δ hoặc Δ', sau đó áp dụng công thức để tìm các nghiệm của phương trình.
Ví dụ: Giải các phương trình sau:
- x² - 3x + 2 = 0
- x² + x - 6 = 0
Hướng dẫn giải:
-
Ta có Δ = (-3)² - 4 . 2 = 1. Vậy nghiệm của phương trình là: x1 = (3 + 1) / 2 = 2 x2 = (3 - 1) / 2 = 1
-
Ta có Δ = 1² - 4 . (-6) = 25. Vậy nghiệm của phương trình đã cho là: x1 = (-1 + 5) / 2 = 2 x2 = (-1 - 5) / 2 = -3
Một số trường hợp đặc biệt của phương trình bậc 2 không chứa tham số:
-
Trường hợp 1: Phương trình khuyết hạng tử Phương trình khuyết hạng tử có dạng: ax² + c = 0 => x² = -c/a => Nếu -c/a > 0 thì nghiệm của phương trình là x = ±√(-c/a) => Nếu -c/a < 0 thì phương trình vô nghiệm => Nếu -c/a = 0 thì phương trình có nghiệm x = 0
Phương trình khuyết hạng tử tự do có dạng: ax² + bx = 0 Phương pháp: Ta đặt x là nhân tử chung. Lúc này, phương trình được chuyển về dạng: x.(ax + b) = 0 Nghiệm của phương trình là:
- x = 0
- x = -b/a
-
Trường hợp 2: Phương trình đưa về dạng bậc 2. Phương trình dạng phương trình trùng phương: ax⁴ + bx² + c = 0 (a≠0) Phương pháp làm:
- Đặt t = x² (thỏa điều kiện: t ≥ 0).
- Phương trình đã cho về dạng phương trình mới: at² + bt + c = 0
- Giải giống như phương trình bậc 2 bình thường. Lưu ý khi tìm nghiệm phải thỏa mãn t ≥ 0
Phương trình có chứa ẩn ở mẫu: Phương pháp làm:
- Tìm điều kiện để phương trình xác định (điều kiện có mẫu số khác 0).
- Thực hiện quy đồng để khử mẫu.
- Giải phương trình mới vừa nhận được. Khi tìm được nghiệm, lưu ý so sánh với điều kiện ban đầu.
Lưu ý: Phương pháp giải phương trình trung phương đặt t = x² (t ≥ 0) còn được gọi là phương pháp đặt ẩn phụ. Bên cạnh đó, phương pháp này không phải lúc nào cũng cứng nhắc chỉ được đặt t = x², bạn cũng cần khéo léo lựa chọn ẩn phụ sao cho vừa đưa về dạng phương trình bậc 2, vừa tạo ra phương trình mới tối giản nhất. Ví dụ, có thể đặt ẩn phụ có dạng t = x + 1, t = x² + x, t = x² - 1… tùy từng bài toán khác nhau.
Dạng 2: Phương trình bậc 2 một ẩn có chứa tham số
Biện luận tham số về số nghiệm của phương trình bậc 2
Phương pháp giải: Sử dụng công thức tính Δ theo tham số m. Sau đó xét dấu của Δ để biện luận số nghiệm của phương trình theo m:
- Δ < 0: phương trình bậc 2 vô nghiệm
- Δ = 0: phương trình bậc 2 có nghiệm kép (1 nghiệm)
- Δ > 0: phương trình bậc 2 có 2 nghiệm phân biệt
Ví dụ: Giải và biện luận số nghiệm của phương trình: mx² - 5x - m - 5 = 0 theo m
Hướng dẫn giải:
- Xét trường hợp m = 0, khi đó phương trình có dạng -5x - 5 = 0 => x = -1
- Xét trường hợp m ≠ 0, khi đó phương trình là phương trình bậc 2 Ta có: Δ = (-5)² - 4m(-m - 5) = (2m + 5)² Vì Δ ≥ 0 nên phương trình trên luôn có nghiệm Trong trường hợp Δ = 0 => m = -5/2, phương trình có 1 nghiệm duy nhất Δ > 0 => m ≠ -5/2, phương trình có 2 nghiệm phân biệt. Nghiệm của phương trình là:
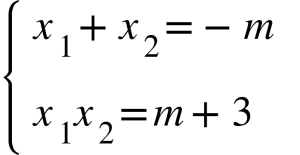
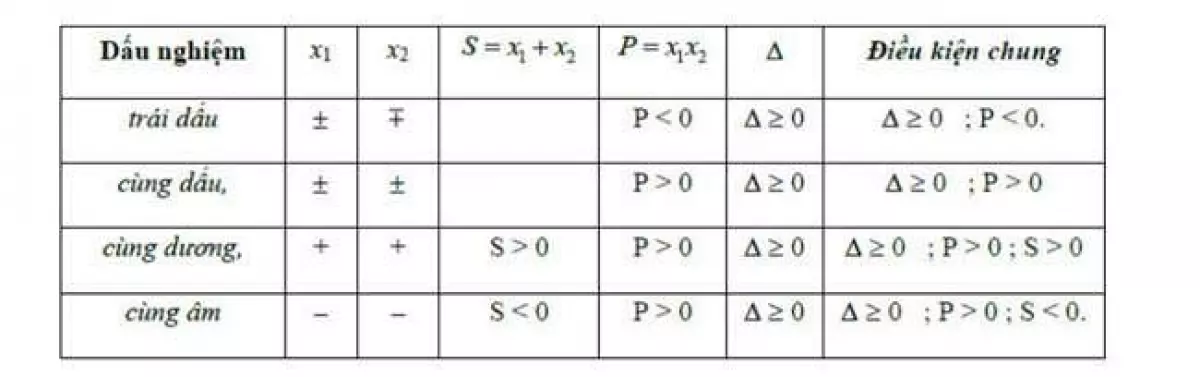
Bên cạnh đó, để tìm điều kiện của tham số thỏa mãn yêu cầu của đề bài, cần thực hiện các bước sau:
- Tính Δ, tìm điều kiện để phương trình có nghiệm (Δ không âm)
- Dựa trên định lý Vi-et, ta có được các hệ thức giữa tích và tổng của nghiệm, từ đó biện luận nghiệm của phương trình đã cho.
Ví dụ: Cho phương trình bậc 2 có dạng x² + mx + m + 3 = 0. Tìm m để phương trình trên có 2 nghiệm thỏa mãn điều kiện sau:
Hướng dẫn giải: Để phương trình trên có nghiệm <=> Δ không âm Vậy ta có: Δ = m² - 2m - 6 = 9 => m = 5 hoặc m = -3 Thay thế m vào Δ ta có: Khi m = 5 => Δ = -7 < 0 (loại) Khi m = -3 => Δ = 9 > 0 (thỏa mãn điều kiện) Vậy khi m = -3 thì phương trình x² + mx + m + 3 = 0 có 2 nghiệm thỏa mãn yêu cầu như đề bài ra.
Trên đây là toàn bộ kiến thức cần nắm về cách giải phương trình bậc 2. Hy vọng với bài viết trên sẽ giúp bạn nắm bắt kiến thức và đạt kết quả tốt nhất trong các kì thi sắp tới.












