Trong bài viết này, chúng ta sẽ tìm hiểu về cách giải phương trình bậc 4 một cách dễ hiểu nhất. Bài viết sẽ giới thiệu 4 phương pháp giải cho 4 dạng phương trình khác nhau. Mỗi phương pháp sẽ được đi kèm với cách giải cụ thể và các bài tập áp dụng giúp bạn hiểu sâu về cách giải phương trình bậc 4.
Cách giải phương trình trùng phương
A. Phương pháp giải
Giải phương trình trùng phương có dạng ax4 + bx2 + c = 0 (a ≠ 0) (1)
Bước 1: Đặt x2 = t (t ≥ 0), ta được phương trình bậc hai ẩn t: at2 + bt + c = 0 (a ≠ 0) (2)
Bước 2: Giải phương trình bậc hai ẩn t.
Bước 3: Giải phương trình x2 = t để tìm nghiệm.
Bước 4: Kết luận.
Biện luận số nghiệm của phương trình trùng phương
- Phương trình (1) có 4 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm dương phân biệt.
- Phương trình (1) có 3 nghiệm phân biệt ⇒ phương trình (2) có 1 nghiệm dương và một nghiệm t = 0.
- Phương trình (1) có 2 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm trái dấu hoặc có nghiệm kép dương.
- Phương trình (1) có duy nhất 1 nghiệm ⇒ phương trình (2) có nghiệm kép x = 0 hoặc có một nghiệm x = 0 và một nghiệm âm.
- Phương trình (1) vô nghiệm ⇒ phương trình (2) vô nghiệm hoặc có hai nghiệm âm.
B. Các ví dụ điển hình
Ví dụ 1: Số nghiệm của phương trình x4 - 6x2 + 8 = 0 là:
Lời giải
Chọn D

Ví dụ 2: Phương trình x4 + 2(m + 1)x2 + m2 = 0 vô nghiệm khi:

Lời giải
Chọn B

Ví dụ 3: Cho phương trình x4 - 2(m + 1)x2 + 2m + 3 = 0 là tham số. Tìm số tự nhiên m nhỏ nhất để phương trình có bốn nghiệm phân biệt.
Lời giải
Chọn A

C. Bài tập vận dụng
Bài 1: Phương trình x4 - 8x2 + 4 = 0 có tập nghiệm là
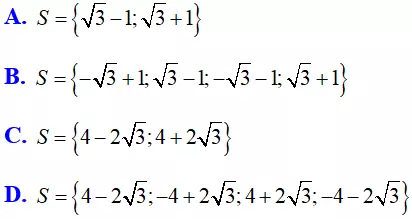
Lời giải:
Chọn B

Bài 2: Số nghiệm của phương trình (x2 - 3x)2 - 2x2(1 - 3x) = 8 là:
Lời giải:
Chọn B

Bài 3: Cho các phương trình. Số nghiệm của các phương trình theo thứ tự là:
Lời giải:
Chọn D

Bài 4: Chọn kết luận đúng về phương trình (1).
Lời giải:
Chọn A

Bài 5: Cho phương trình m2x4 + x2 - m2 - 1 = 0 với m là tham số. Chọn khẳng định sai.
Lời giải:
Chọn A

Bài 6: Phương trình có nghiệm là:
Lời giải:
Chọn

Bài 7: Tìm m để phương trình (m + 1)x4 + 5x2 - m - 1 = 0. Tìm giá trị của m để phương trình có đúng hai nghiệm phân biệt.
Lời giải:
Chọn D

Bài 8: Cho phương trình x4 - 13x2 + m = 0 (1). Với giá trị của m để phương trình (1) có ba nghiệm phân biệt, ba nghiệm đó là:
Lời giải:
Chọn C

Bài 9: Tìm m để phương trình x4 + 2mx2 + 8 = 0 có bốn nghiệm phân biệt sao cho tổng của bình phương các nghiệm bằng 32
Lời giải:
Chọn C

Bài 10: Điều kiện của a và b để phương trình x4 - 2(a2 + b2)x2 + (a2 - b2)2 = 0 có ba nghiệm phân biệt là:
Lời giải:
Chọn D
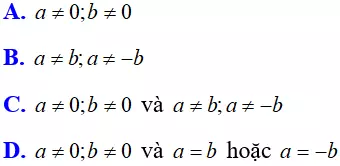
A. Phương pháp giải
Vì x = 0 không là nghiệm của phương trình (1) nên chia hai vế của (1) cho x2 ta được
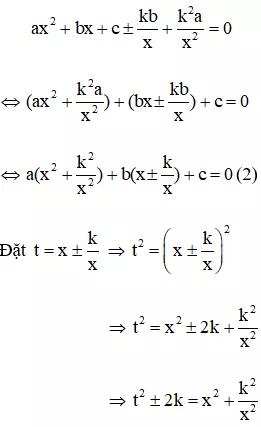
Thay vào phương trình (2) ta có:
Giải phương trình trên tìm t rồi sau đó tìm x
Bài tập
Câu 1: Giải phương trình x4 + 4 = 5x(x2 - 2)
Giải
Phương trình (1) ⇔ x4 + 4 = 5x3-10x ⇔ x4 - 5x3 + 10x + 4 = 0
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được:
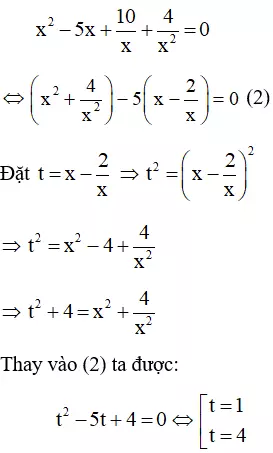
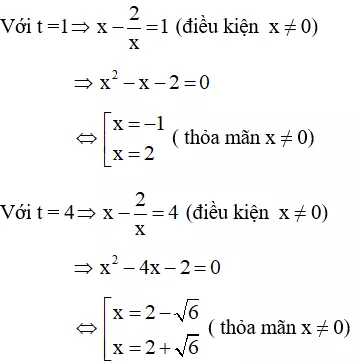
Vậy phương trình có 4 nghiệm: x = -1, x = 2, x = 2 ± √6
Câu 2: Giải phương trình x4 + 9 = 5x(x2 - 3)
Giải
Phương trình (1) ⇔ x4 + 9 = 5x3 - 15x ⇔ x4 - 5x3 + 15x + 9 = 0
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được
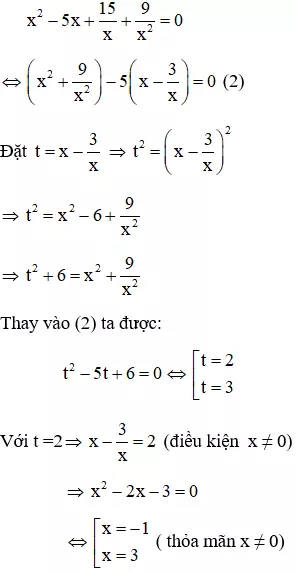
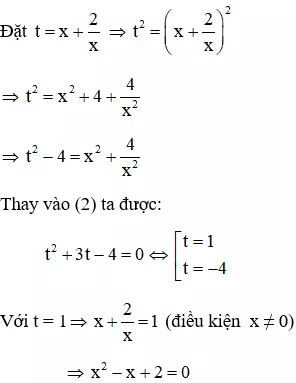
Câu 3: Giải phương trình x4 + 4 = -3x3 - 6x
Giải
Phương trình x4 + 4 = -3x3 - 6x ⇔ x4 + 3x3 + 6x + 4 = 0 (1)
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được
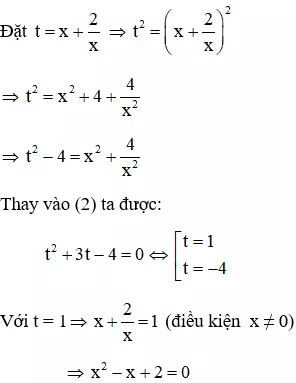
(phương trình vô nghiệm vì ∆ = (-1)2 - 4.1.2 = -7 < 0)
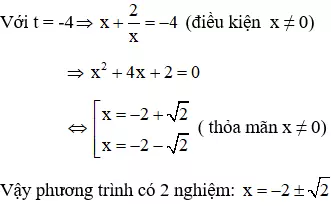
Câu 4: Giải phương trình x4 + 4x3 - 8x + 4 = 0 (1)
Giải
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được
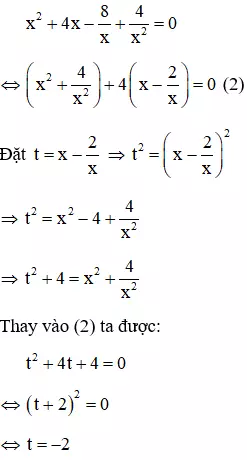
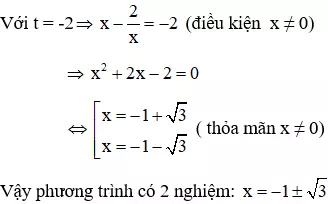
Câu 5: Giải phương trình x4 + 5x3 + 2x2 - 35x + 49 = 0 (1)
Giải
Vì x = 0 không là nghiệm của phương trình (1) nên chia cả hai vế của (1) cho x2 ta được
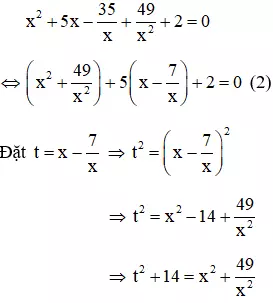
Thay vào (2) ta được: t2 + 5t + 16 = 0
Phương trình trên có ∆ = 52 - 4.1.16 = 25 - 64 = -39 < 0 nên phương trình vô nghiệm
Vậy phương trình (1) vô nghiệm
A. Phương pháp giải
- B1: Đặt t = (x + a)(x + b) ⇒ t = x2 + (a + b)x + ab
- B2: Biến đổi biểu thức (x + c)(x + d) theo biến t
- Ta có: (x + c)(x + d) = x2 + (c + d)x + cd = x2 + (a + b)x + cd = t - ab + cd
- B3: Biến đổi phương trình (x + a)(x + b)(x + c)(x + d) = m theo biến t
- t(t - ab + cd) = m ⇔ t2 + (- ab + cd)t - m = 0(*)
- Giải phương trình (*) tìm t sau đó tìm x
Bài tập
Câu 1: Giải phương trình x(x + 1)(x + 2)(x + 3) = 24 (1)
Giải
Phương trình (1) ⇔ x(x + 3)(x + 1)(x + 2) = 24
Đặt t = x(x + 3) = x2 + 3x
(x + 1)(x + 2) = x2 + 3x + 2 = t + 2
Khi đó phương trình trở thành:
Với t = -6 ⇒ x2 + 3x = -6 ⇔x2 + 3x + 6 = 0 (phương trình vô nghiệm vì ∆ < 0)
Với t = 4 ⇒ x2 + 3x = 4 ⇔x2 + 3x - 4 = 0. Phương trình có a + b + c = 0 nên có 2 nghiệm x = 1, x = -4
Vậy phương trình có 2 nghiệm: x = 1, x = -4
Câu 2: Giải phương trình (x + 4)(x + 5)(x + 7)(x + 8) = 4 (1)
Giải
Phương trình (1) ⇔ (x + 4)(x + 8)(x + 5)(x + 7) = 4
Đặt t = (x + 4)(x + 8) = x2 + 12x + 32
(x + 5)(x + 7) = x2 + 12x + 35 = t + 3
Khi đó phương trình trở thành:
Với t = 1 ⇒ x2 + 12x + 32 = 1 ⇔ x2 + 12x + 31 = 0. Phương trình có ∆ > 0 nên có 2 nghiệm phân biệt: x = -6 ± √5
Với t = -4 ⇒ x2 + 12x + 32 = -4 ⇔ x2 + 12x + 36 = 0 ⇔(x + 6)2 = 0 ⇔ x = -6
Vậy phương trình có 3 nghiệm: x = -6, x = -6 ± √5
Câu 3: Giải phương trình (x + 5)(x + 6)(x - 4)(x - 5) = -21 (1)
Giải
Phương trình (1) ⇔ (x + 5)(x - 4)(x + 6)(x - 5) = -21
Đặt t = (x -4)(x + 5) = x2 + x - 20
(x + 6)(x - 5) = x2 + x - 30 = t - 10
Khi đó phương trình trở thành:
Với t = 3 ⇒ x2 + x-20 = 3 ⇔ x2 + x - 23 = 0. Phương trình có ∆ > 0 nên phương trình có 2 nghiệm phân biệt
Với t = 7 ⇒ x2 + x-20 = 7 ⇔ x2 + x - 27 = 0. Phương trình có ∆ > 0 nên phương trình có 2 nghiệm phân biệt
Vậy phương trình có 4 nghiệm:
Câu 4: Giải phương trình (x +5)(x + 4)(x - 1)(x - 2) = 112 (1)
Giải
Phương trình (1) ⇔ (x +5)(x - 2)(x + 4)(x - 1) = 112
Đặt t = (x -2)(x + 5) = x2 + 3x - 10
(x + 4)(x - 1) = x2 + 3x + 2 = t + 6
Khi đó phương trình trở thành:
Với t = 8 ⇒ x2 + 3x - 10 = 8 ⇔ x2 + 3x - 18 = 0. Phương trình có ∆ > 0 nên phương trình có 2 nghiệm phân biệt: x = -6, x = 3
Với t = -14 ⇒ x2 + 3x - 10 = -14 ⇔ x2 + 3x + 4 = 0. Phương trình có ∆ < 0 nên phương trình vô nghiệm
Vậy phương trình có 2 nghiệm: x = -6, x = 3
Câu 5: Giải phương trình (x +1)(x + 3)(x + 6)(x + 4) = -8 (1)
Giải
Phương trình (1) ⇔ (x +1)(x + 6)(x + 4)(x + 3) = -8
Đặt t = (x + 1)(x + 6) = x2 + 7x + 6
(x + 4)(x + 3) = x2 + 7x + 12 = t + 6
Khi đó phương trình trở thành:
Với t = -2 ⇒ x2 + 7x + 6 = -2 ⇔ x2 + 7x + 8 = 0. Phương trình có ∆ > 0 nên phương trình có 2 nghiệm phân biệt
Với t = -4 ⇒ x2 + 7x + 6 = -4 ⇔ x2 + 7x + 10 = 0. Phương trình có ∆ < 0 nên phương trình vô nghiệm
Vậy phương trình có nghiệm duy nhất x = -4
Trong bài viết này, chúng ta đã tìm hiểu về cách giải phương trình bậc 4 dễ hiểu nhất. Đối với từng dạng phương trình, chúng ta đã có cách giải cụ thể và áp dụng các bài tập để tăng cường kiến thức. Hy vọng rằng thông qua bài viết này, bạn đọc có thể nắm bắt được cách giải phương trình bậc 4 một cách nhanh chóng và chính xác.












