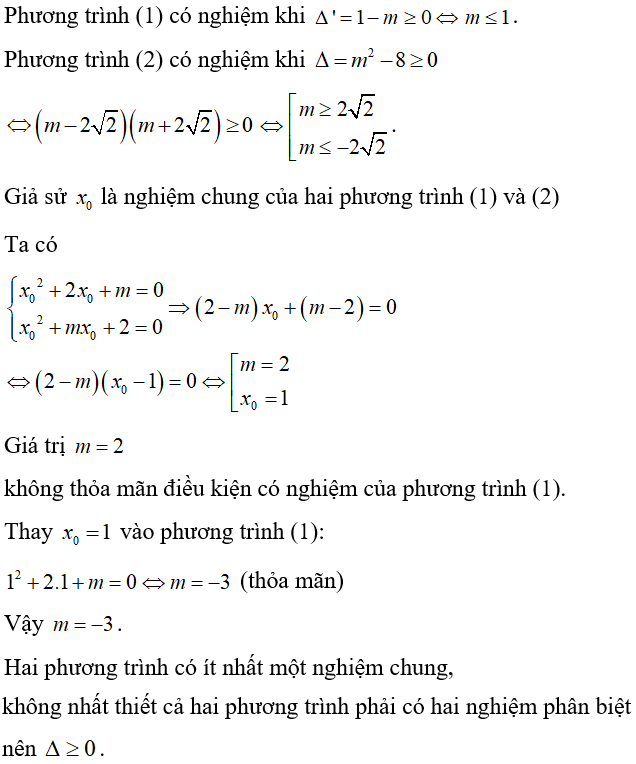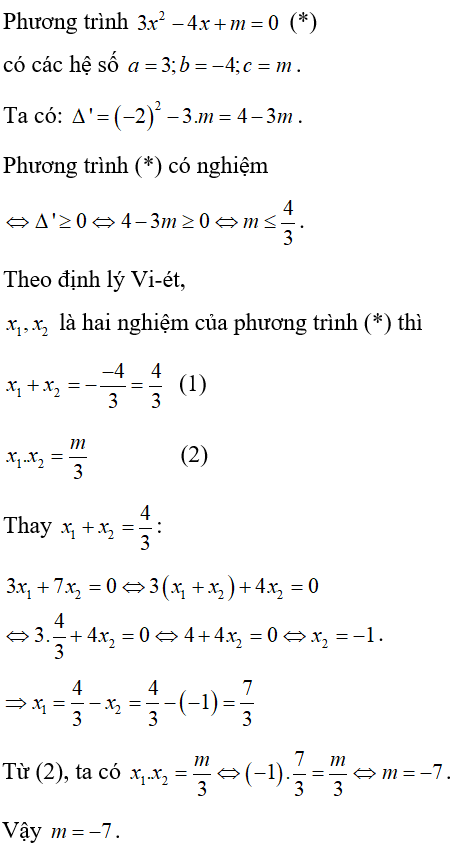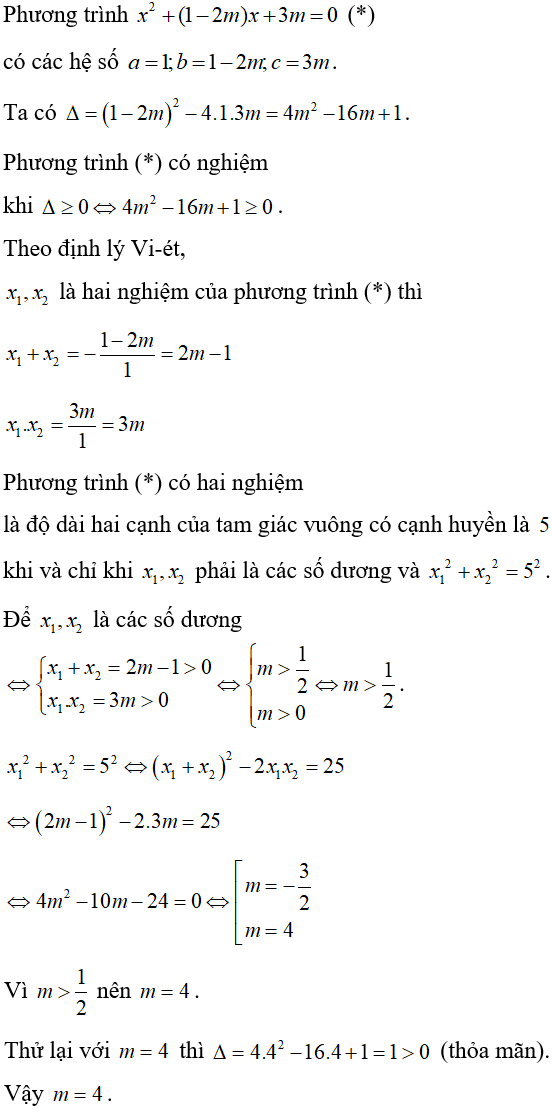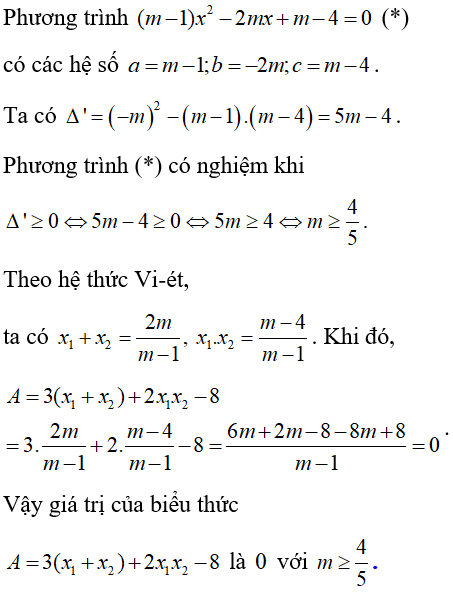A. Phương pháp giải
Dạng 3.1: Giải và biện luận phương trình theo tham số m
- Bước 1: Xác định các hệ số a, b, c (hoặc a, b', c).
- Bước 2: Giải phương trình theo m:
- Với giá trị của m mà a = 0, giải phương trình bậc nhất.
- Với giá trị của m mà a ≠ 0, giải phương trình bậc hai: Tính Δ = b'2 - ac (hoặc Δ' = b2 - 4ac), xét các trường hợp của Δ chứa tham số và tìm nghiệm theo tham số.
- Bước 3: Kết luận.
Biện luận phương trình:
- Phương trình có nghiệm khi:
- Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.
- Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm.
- Phương trình có một nghiệm khi:
- Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.
- Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm kép.
- Phương trình có hai nghiệm phân biệt khi: Giá trị của m mà a ≠ 0, phương trình bậc hai có hai nghiệm phân biệt.
Dạng 3.2: Xác định dấu các nghiệm của phương trình
- Bước 1: Xác định hệ số.
- Bước 2: Tính Δ = b2 - 4ac (hoặc Δ' = b2 - 4ac) để kiểm tra phương trình có nghiệm hay không.
- Bước 3: Trong trường hợp phương trình có nghiệm (Δ ≥ 0 hoặc Δ' ≥ 0), tính tổng S và tích P của hai nghiệm theo định lý Vi-ét để xét dấu các nghiệm của phương trình.
- Phương trình có hai nghiệm cùng dấu: P > 0.
- Phương trình có hai nghiệm dương: .
- Phương trình có hai nghiệm âm: .
- Phương trình có hai nghiệm trái dấu: P < 0. Chú ý: Phương trình có hai nghiệm trái dấu chỉ cần xét P < 0 hoặc a.c < 0.
- Bước 4: Kết luận.
Dạng 3.3: Tìm m để phương trình có nghiệm thỏa mãn điều kiện cho trước
Dạng 3.3.1: Tìm m để phương trình có nghiệm thỏa mãn điều kiện về dấu hoặc thỏa mãn đẳng thức, bất đẳng thức liên hệ giữa các nghiệm
- Bước 1: Tìm điều kiện a ≠ 0 (nếu cần) và điều kiện để phương trình có nghiệm.
- Bước 2: Tính tổng S và tích P của hai nghiệm theo định lý Vi-ét.
- Bước 3: Sử dụng hệ thức Vi-ét, kết hợp biến đổi đẳng thức, bất đẳng thức để tìm tham số.
- Bước 4: Đối chiếu điều kiện và kết luận.
Dạng 3.3.2: Tìm tham số m để phương trình có một nghiệm là x0
- Bước 1: Thay giá trị x0 vào phương trình để tìm tham số.
- Bước 2: Thay giá trị của tham số vào phương trình hoặc hệ thức Vi-ét để tìm nghiệm còn lại.
- Bước 3: Kết luận.
Dạng 3.3.3: Tìm giá trị của tham số để hai phương trình có ít nhất một nghiệm chung
- Bước 1: Tìm điều kiện để các phương trình có nghiệm.
- Bước 2: Tìm nghiệm chung và tìm tham số: Có thể giả sử x0 là nghiệm chung, lập hệ phương trình trình hai ẩn (x0 và tham số) và giải hệ phương trình.
- Bước 3: So sánh với điều kiện và kết luận.
B. Các ví dụ điển hình
Ví dụ 1: Giải phương trình x2 - 2x + 1 - m2 = 0 với m là tham số, m ≠ 0. 
Ví dụ 2: Cho phương trình x2 + √7x + 1 = 0. Khẳng định nào sau đây là đúng? 
Ví dụ 3: Số các giá trị nguyên của tham số m để phương trình x2 - 2x + m = 0 có hai nghiệm phân biệt x1; x2 sao cho x12.x22 ≤ 4 là:. Lời giải: Chọn B
Ví dụ 4: Phương trình bậc hai mx2 + (2m + 1)x + 3 = 0 có một nghiệm là x = -1. Giá trị của m và nghiệm còn lại là: Lời giải: Chọn A
Ví dụ 5: Cho hai phương trình bậc hai x2 + 2x + m = 0 (1) và x2 + mx + 2 = 0 (2) (với m là tham số). Tìm m để hai phương trình có ít nhất một nghiệm chung. Lời giải: Chọn B
C. Bài tập vận dụng
Bài 1: Cho phương trình bậc hai (m - 1)x2 - 2mx + m + 2 = 0 (với m là tham số). Giải phương trình trong trường hợp m < 2. Lời giải: Chọn C
Bài 2: Cho m là số nguyên để phương trình 2x2 - 4x + m - 3 = 0 có hai nghiệm phân biệt cùng dấu. Giá trị của biểu thức là: Lời giải: Chọn B
Bài 3: Phương trình 2x2 + (m - 1)x + 2m + 4 = 0 có một nghiệm bằng 5. Nghiệm còn lại của phương trình là: Lời giải: Chọn B
Bài 4: Với giá trị nào của m thì hai phương trình x2 - mx + m + 1 = 0 (1) và x2 - (m - 2)x + m - 3 = 0 (2) có ít nhất một nghiệm chung ? Lời giải: Chọn C
Bài 5: Giá trị nguyên dương của m để phương trình 2x2 - 4x + m = 0 có hai nghiệm dương phân biệt là: Lời giải: Chọn D
Bài 6: Tìm giá trị của tham số m để phương trình 3x2 - 4x + m = 0 có hai nghiệm x1; x2 thỏa mãn 3x1 + 7x2 = 0. Lời giải: Chọn A
Bài 7: Tìm m để phương trình x2 + (1 - 2m)x + 3m = 0 có hai nghiệm x1, x2 là độ dài hai cạnh của tam giác vuông có cạnh huyền là 5. 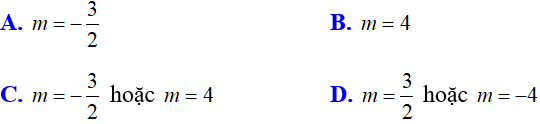
Bài 8: Cho phương trình (m - 1)x2 - 2mx + m - 4 = 0(m là tham số, m ≠ 0). Gọi x1, x2 là hai nghiệm của phương trình. Giá trị của biểu thức A = 3(x1 + x2) + 2x1x2 - 8 là: 
Bài 9: Cho phương trình bậc hai x2 - mx + m - 1 = 0 (với m là tham số). Gọi x1, x2 là hai nghiệm của phương trình. Tìm m để đạt giá trị lớn nhất. 
Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có đáp án khác.