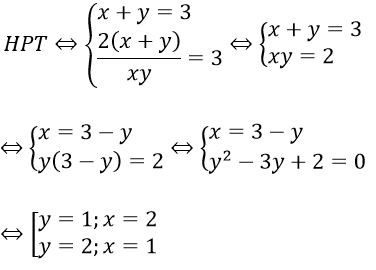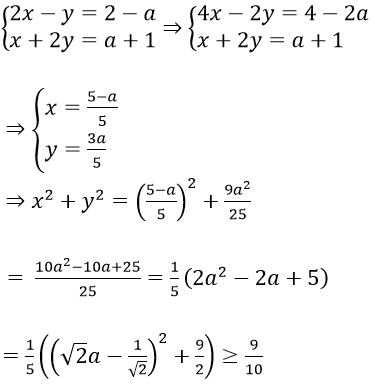Bài viết này sẽ giới thiệu về cách giải và biện luận hệ phương trình bậc nhất, cung cấp những phương pháp giải chi tiết để học sinh có thể ôn tập và làm bài tập một cách hiệu quả. Chúng ta sẽ khám phá lý thuyết và phương pháp giải cho các loại hệ phương trình bậc nhất, và cùng nhau tìm hiểu về biểu diễn hình học của tập nghiệm. Hãy bắt đầu!
Cách giải và biện luận hệ phương trình bậc nhất (cực hay)
Lý thuyết & Phương pháp giải
1. Phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn có dạng tổng quát là ax + by = c, trong đó a, b, c là các hệ số và a, b không đồng thời bằng 0.
CHÚ Ý:
- Khi a = b = 0, phương trình vô nghiệm nếu c ≠ 0, còn nếu c = 0 thì mọi cặp số (x0; y0) đều là nghiệm.
- Khi b ≠ 0, phương trình
ax + by = ctrở thànhy = (-a/b)x + c/b. Cặp số (x0; y0) là nghiệm của phương trình (1) khi và chỉ khi điểm M(x0; y0) thuộc đường thẳng (2).
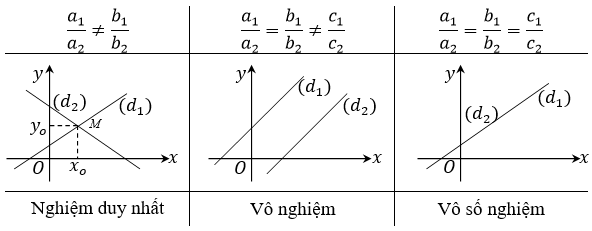
Từ đó, chúng ta có thể chứng minh rằng phương trình bậc nhất hai ẩn luôn có vô số nghiệm và biểu diễn hình học của nghiệm là một đường thẳng trong mặt phẳng tọa độ Oxy.
2. Hệ hai phương trình bậc nhất hai ẩn
Hệ phương trình bậc nhất hai ẩn có dạng tổng quát là:
{ a1x + b1y = c1
{ a2x + b2y = c2Nếu cặp số (x0; y0) đồng thời là nghiệm của cả hai phương trình của hệ thì (x0; y0) được gọi là một nghiệm của hệ phương trình (1). Để giải hệ phương trình này, chúng ta sử dụng quy tắc Cramé.
Xét DKết quả:
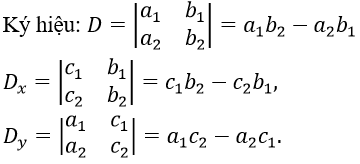
- D ≠ 0: Hệ có nghiệm duy nhất x = Dx/D, y = Dy/D.
- D = 0:
- Dx ≠ 0 hoặc Dy ≠ 0: Hệ vô nghiệm.
- Dx = Dy = 0: Hệ có vô số nghiệm.
Có nhiều cách giải hệ phương trình bậc nhất hai ẩn như phương pháp thế, phương pháp cộng đại số. Biểu diễn hình học của tập nghiệm được thể hiện qua việc đi qua hai đường thẳng.
3. Hệ ba phương trình bậc nhất ba ẩn
Phương trình bậc nhất ba ẩn có dạng tổng quát là ax + by + cz = d, trong đó x, y, z là ba ẩn; a, b, c, d là các hệ số và a, b, c không đồng thời bằng 0.
Hệ phương trình bậc nhất ba ẩn có dạng tổng quát là:
{ a1x + b1y + c1z = d1
{ a2x + b2y + c2z = d2
{ a3x + b3y + c3z = d3Mỗi bộ ba số (x0, y0, z0) nghiệm đúng của ba phương trình của hệ được gọi là một nghiệm của hệ phương trình (2). Để giải hệ phương trình này, ta có thể sử dụng phương pháp khử bớt ẩn, cộng đại số hoặc phương pháp thế.
Ví dụ minh họa
Bài 1: Giải hệ phương trình
Lời giải:
a. Ta có: y = 1-√2x ⇒ 3x + √2(1-√2.x) = 2 ⇒ x = 2 - √2 ⇒ y = 3 - 2√2
b. Ta có: Thế y = 4 - 2x vào phương trình y + z = 2 + √2 ta được -2x + z = -2 + √2
Giải hệ ta được x = 1; z = √2 ⇒ y = 2
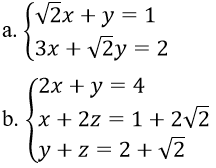
Bài 2: Giải hệ phương trình
Lời giải:
ĐK: xy ≠ 0. Khi đó
Bài 3: Có bao nhiêu cặp số nguyên (a; b) sao cho hệ phương trình vô nghiệm
Lời giải: Ta có ax + y = 2 ⇒ y = 2 - ax Thay vào phương trình 6x + by = 6 có 6x + b(2-ax) = 6 ⇔ x(6-ab) + 2b - 6 = 0 Hệ vô nghiệm khi và chỉ khi phương trình x(6-ab) + 2b - 6 = 0 vô nghiệm. Do (a; b) nguyên nên (a; b) = {(6; 1); (1; 6); (-6; -1); (-1; -6); (-2; -3); (-3; -2); (3; 2)}
Bài 4: Gọi (x0; y0; z0) là nghiệm của hệ phương trình
Tính giá trị của biểu thức P = x0y0z0
Lời giải:
Ta có
Phương trình (3) ⇔ z = 24 - 3x - 2y. Thay vào (1) và (2) ta được hệ phương trình
Suy ra z = 24 - 3.4 - 2.5 = 2
Vậy hệ phương trình có nghiệm (x; y; z) = (4; 5; 2) → P = 4.5.2 = 40
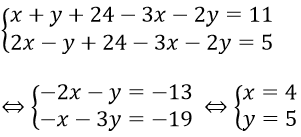
Bài 5: Tìm giá trị thực của tham số m để hệ phương trình có duy nhất một nghiệm.
Lời giải: Từ hệ phương trình đã cho ta suy ra Hệ phương trình Có nghiệm duy nhất khi (1; -2) là nghiệm của phương trình 2mx + 5y - m = 0 tức là 2m.1 + 5.(-2) - m = 0 ⇔ m = 10
Bài 6: Cho hệ phương trình. Tìm các giá trị thích hợp của tham số a để tổng bình phương hai nghiệm của hệ phương trình đạt giá trị nhỏ nhất.
Lời giải:
Ta có:
Đẳng thức xảy ra khi a = 1/2
Trên đây là những phương pháp giải chi tiết cho các loại hệ phương trình bậc nhất. Hy vọng rằng thông qua bài viết này, các bạn sẽ có cái nhìn tổng quan và hiểu rõ hơn về cách giải và biện luận hệ phương trình bậc nhất. Chúc các bạn học tốt và thành công trong việc ôn tập và làm bài tập!
