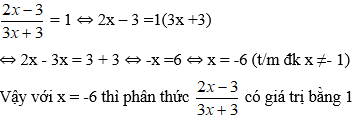Có thể bạn đang gặp khó khăn trong việc tìm giá trị của biến x để phân thức có giá trị bằng. Trong bài viết này, chúng ta sẽ cùng nhau khám phá cách giải bài tập này một cách dễ dàng và nhanh chóng.
A. Phương pháp giải
Bước 1: Tìm điều kiện để phân thức có nghĩa. Điều kiện này thường bao gồm những giá trị của biến x mà khi thay vào phân thức sẽ không làm phân thức trở thành vô nghĩa.
Bước 2: Vận dụng các tính chất của phân thức để khử dạng phân thức, đưa bài toán về dạng tìm x.
Bước 3: Đối chiếu giá trị của biến tìm được với điều kiện đã tìm được và trả lời.
B. Ví dụ minh họa
Ví dụ 1: Với giá trị nào của x để phân thức có giá trị bằng 1.
Lời giải: Phân thức xác định khi 3x + 3 ≠ 0 ⇔ 3x ≠ -3 ⇔ x ≠ -1
Ví dụ 2: Với giá trị nào của x để phân thức có giá trị bằng 0.
Lời giải: Điều kiện để phân thức xác định: 2x - x^2 - 1 ≠ 0 ⇔ -(x - 1)^2 ≠ 0 ⇔ x ≠ 1 = 0 ⇔ x - 2 = 0 ⇔ x = 2 (tm đk x ≠ 1) Vậy với x = 2 thì phân thức có giá trị bằng 0.
Ví dụ 3: Cho biểu thức. Tìm x để image.
Lời giải:
C. Bài tập vận dụng
Bài 1: Với giá trị nào của x để A. 1 B. 2 C. -5 D. -3
Lời giải: Đáp án: C. ĐKXĐ: x ≠ 3
Bài 2: Với giá trị nào của x để A. 2 B. -2 C. 8 D. -8
Lời giải: Đáp án: C ĐKXĐ: x ≠ -4
Bài 3: Với giá trị nào của x để A. 5 B. -5 C. 2 D. -2
Lời giải: Đáp án: B. ĐKXĐ: x ≠ - 2
Bài 4: Với giá trị nào của x để A. 1 B. 2 C. -1/2 D. -3/2
Lời giải: Đáp án: C ĐKXĐ: x ≠ -1; x ≠ 0. Ta có:
Bài 5: Với giá trị nào của x để A. 7 B. 5 C. 3 D. -1
Lời giải: Đáp án: A ĐKXĐ: x ≠ 3; x ≠ 5. Ta có:
Bài 6: Cho biểu thức. Tìm x để A = 0
Lời giải:
Bài 7: Cho biểu thức
Lời giải:
Bài 8: Tìm giá trị của x để phân thức có giá trị bằng 2
Lời giải:
Bài 9: Cho biểu thức. Tìm x để P = 5
Lời giải:
Bài 10: Cho biểu thức. Tìm x để Q = 1
Lời giải:
Sau khi đã tìm hiểu cách giải bài tập tìm giá trị của biến x để phân thức có giá trị bằng, hy vọng rằng bạn đã nắm vững kiến thức và có thể áp dụng vào các bài tập khác. Cố gắng làm nhiều bài tập và ôn tập thường xuyên để nâng cao khả năng giải toán của mình. Chúc bạn thành công!