Mặt phẳng trung trực là gì?
1.1. Định nghĩa
Trong không gian, mặt phẳng trung trực của một đoạn thẳng AB là mặt phẳng (P) đi qua trung điểm I của đoạn thẳng AB và vuông góc với đường thẳng AB.
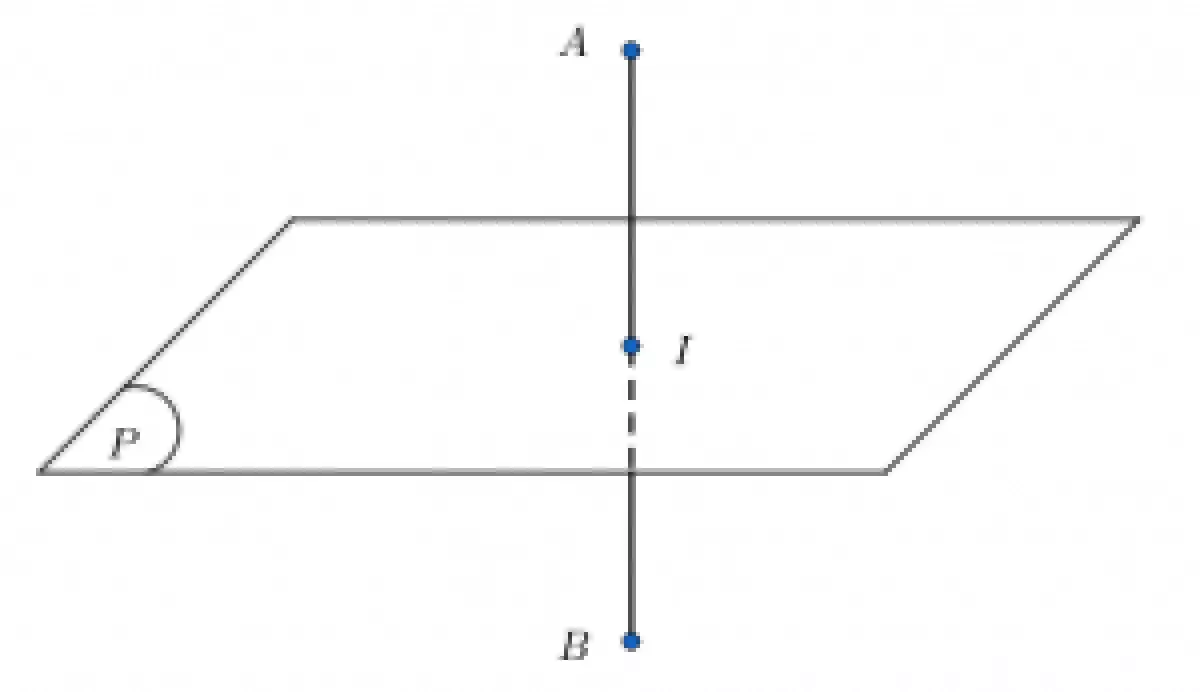
1.2. Tính chất:
Mọi điểm trên mặt phẳng trung trực cách đều hai đầu đoạn thẳng.
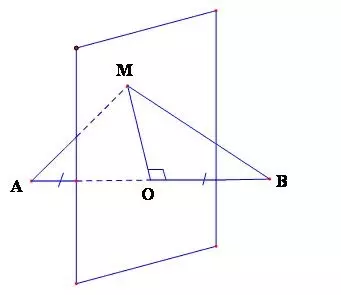
Như vậy, khái niệm mặt phẳng trung trực tương tự với khái niệm đường trung trực của đoạn thẳng trong mặt phẳng.
2. Cách viết phương trình mặt phẳng trung trực của đoạn thẳng
Chúng ta đã hiểu về mặt phẳng trung trực của đoạn thẳng và để viết phương trình mặt phẳng trung trực trong không gian, chúng ta sẽ dựa vào khái niệm này.
Theo định nghĩa đã nêu, nếu (P) là mặt phẳng trung trực của đoạn AB, thì vector AB chính là vector pháp tuyến của mặt phẳng (P) và trung điểm I của đoạn AB là một điểm thuộc mặt phẳng (P).
Khi đó, phương trình mặt phẳng trung trực (P) đoạn thẳng AB được viết theo 3 bước sau:
- Bước 1: Tìm tọa độ trung điểm I của đoạn thẳng AB (lấy trung bình cộng tọa độ điểm A và điểm B).
- Bước 2: Tìm vector AB (lấy tọa độ điểm cuối B trừ đi tọa độ điểm đầu A). Ta sẽ có vector pháp tuyến của mặt phẳng (P).
- Bước 3: Viết phương trình mặt phẳng (P) đi qua điểm I và nhận vector AB là vector pháp tuyến.
Ví dụ 1: Cho điểm A (2;1;1) và B (2;-1;-1) trong không gian Oxyz. Viết phương trình mặt phẳng trung trực (P) của đoạn AB.
Giải
Gọi I (x,y,z) là trung điểm của AB, khi đó:
- x = (xA + xB)/2 => x = 2
- y = (yA + yB)/2 => y = 0
- z = (zA + zB)/2 => z = 0
Ta có vector AB = (0;-2;-2)
Vậy mặt phẳng trung trực (P) này đi qua điểm I (2;0;0) có vector pháp tuyến n = AB = (0;-2;-2)
Nên (P) có phương trình là: 0(x-2) - 2(y-0)-2(z-0) = 0 <=> y + z = 0
Ví dụ 2: Trong không gian Oxyz, cho điểm A (0;2;-5) và B (2;-4;7). Vậy mặt phẳng trung trực của đoạn thẳng AB có phương trình:
A. 2x - 6y + 12z - 10 = 0 B. -2x + 6y -12z +10 = 0 C. x - 3y +6z -10 = 0 D. -x + 3y - 6z +10 = 0
Giải
Trung điểm I của đoạn thẳng AB có tọa độ là (1;-1;1)
Véc-tơ AB có tọa độ là (2;-6;12) là một véc-tơ pháp tuyến của mặt phẳng trung trực của đoạn AB.
Mặt phẳng có phương trình dưới đây: 2(x-1) - 6(y+1) +12(z-1) = 0 <=> 2x - 6y + 12z -20 = 0 <=> x - 3y + 6z -10 = 0
Chọn đáp án C
Cách nhẩm nhanh phương trình mặt phẳng trung trực
Khi làm các bài toán trắc nghiệm về viết phương trình mặt phẳng trung trực, ta có thể giản lược các bước trên để nhận kết quả nhanh chóng. Ví dụ:
"Viết phương trình tổng quát (P) biết trong không gian Oxyz, cho điểm A(1;2;3) và điểm B(3;6;1). Biết rằng đoạn thẳng AB nhận mặt phẳng (P) là mặt phẳng trung trực."
-
Đầu tiên, ta nhận véc-tơ AB (2;4;-2). Khi đó, ta có phần của phương trình là: 2x + 4y - 2z + ... = 0
-
Sau đó, ta nhận tọa độ trung điểm AB là I(2;4;2) và thay vào phần phương trình vừa tìm được. Ta có: 2.2 + 4.4 - 2.2 = 16. Lấy phần phương trình trên trừ đi kết quả vừa tìm được: 2x + 4y - 2z -16 = 0
Dưới đây là cách nhẩm nhanh phương trình mặt phẳng trung trực của đoạn thẳng. Hãy luyện tập để làm bài nhanh chóng và thành thạo hơn.
Đăng ký ngay để được tóm tắt kiến thức hình học không gian và xây dựng lộ trình học phù hợp nhất phục vụ quá trình ôn thi tốt nghiệp THPT môn Toán

3. Một số bài tập viết phương trình mặt phẳng trung trực của đoạn thẳng
Bài 1: Cho điểm A(1;2;3) và điểm B(3;6;1) trong không gian Oxyz, ta biết mặt phẳng (P) là mặt phẳng trung trực của đoạn thẳng AB. Viết phương trình tổng quát (P).
Giải: Đoạn thẳng AB có tọa độ (2;4;2) là trung điểm I.
Vectơ AB có tọa độ (2;4;-2) là một vectơ pháp tuyến của mặt phẳng (P).
Phương trình mặt phẳng (P) là: 2(x-2) + 4(y-4) - 2(z-2) = 0 <=> 2x + 4y - 2z - 16 = 0 <=> x - 3y + 6z - 10 = 0
Bài 2: Trong không gian Oxyz, điểm A(-1,2,3) và điểm B(1,6,-1). Phương trình mặt phẳng trung trực AB có dạng như thế nào?
Giải: Trung điểm I của đoạn thẳng AB có tọa độ (0;4;1).
Mặt phẳng trung trực đoạn AB có vector pháp tuyến AB có tọa độ (2;4;-4).
Mặt phẳng ta cần tìm có phương trình như sau: 2(x-0) + 4(y-4) - 4(z-1) = 0 <=> 2x + 4y - 4z - 16 = 0 <=> x - 2y + 2z + 8 = 0
Bài 3: Lập phương trình mặt phẳng có chứa trục Oy, điểm Q(1;4;-3)
(A) Mặt phẳng có chứa trục Oy và Q (1;4;-3) (B) Mặt phẳng có chứa Oy ⇒ vector chỉ phương là j = (0;1;0) (C) Mặt phẳng có chứa O(0;0;0) và Q (1;4;-3) ⇒ nhận OA = (1;4;-3) là một vector chỉ phương (D) ⇒ Mặt phẳng nhận n = [j, OA] = (-3;0;-1) là vector pháp tuyến (E) ⇒ Mặt phẳng (Q): -3(x - 0) - 1.(z - 0) = 0 (F) Hoặc (Q): 3x + z = 0
Bài 4: Đoạn AB có phương trình mặt phẳng trung trực là?
Giải: Gọi trung điểm AB là điểm M.
Ta có tọa độ của M là:
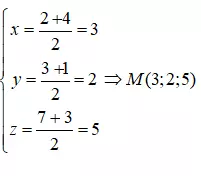
Đoạn thẳng AB có P là mặt phẳng trung trực nên P đi qua M và nhận vector AB là vector pháp tuyến. Vậy phương trình của mặt phẳng P là:
Bài 5: Phương trình tổng quát MP (MNP) với M(1;1;1), N(4;3;2), P(5;2;1) là?
Giải:
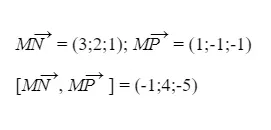
Một vector pháp tuyến của mặt phẳng (MNP) là n (1;-4;5)
Mặt phẳng (MNP) với M(1;1;1), N(4;3;2), P(5;2;1) có phương trình tổng quát là:
(x-1) - 4(y-1) + 5(z-1) = 0 <=> x + 2y - 2z - 6 = 0
Như vậy, đó là toàn bộ kiến thức và tổng hợp đầy đủ các dạng bài tập về phương trình mặt phẳng trung trực. Hy vọng sau bài viết này, bạn có thể áp dụng công thức để giải các bài tập một cách dễ dàng. Để học tập và ôn tập kiến thức lớp 12 ôn thi THPT Quốc gia, hãy truy cập Vuihoc.vn và đăng ký khóa học ngay hôm nay nhé!
Xem thêm:
- Cách xác định góc giữa đường thẳng và mặt phẳng trong không gian
- Phương Trình Đường Thẳng Trong Không Gian: Lý Thuyết Và Bài Tập












