Cây nhị phân là một cấu trúc dữ liệu quan trọng trong lĩnh vực khoa học máy tính. Để làm việc với cây, chúng ta cần có một cơ chế để duyệt qua các phần tử của cây. Quá trình này được gọi là duyệt cây và là chủ đề chính của phần này. Trong cấu trúc dữ liệu tuyến tính như danh sách liên kết, ngăn xếp, hàng đợi, chúng ta có thể truy cập các phần tử theo thứ tự tuần tự. Nhưng trong cây, có nhiều cách khác nhau để duyệt qua các phần tử. Trong bài viết này, chúng ta sẽ tìm hiểu về các phương pháp duyệt cây và cách sắp xếp chúng thành các loại duyệt cụ thể.
Các khả năng duyệt cây
Bắt đầu từ gốc của cây nhị phân, chúng ta có ba bước chính và thứ tự thực hiện chúng xác định phương pháp duyệt. Các bước đó là: thực hiện một hành động trên nút hiện tại (được gọi là "ghé thăm" nút và được ký hiệu là "D"), đi qua cây con bên trái (được ký hiệu bằng "L") và đi qua cây con bên phải (được ký hiệu là "R"). Quá trình này có thể được mô tả dễ dàng thông qua đệ quy. Dựa trên định nghĩa trên, có 6 khả năng duyệt cây:
- Duyệt cây con bên trái, xử lý nút hiện tại và sau đó duyệt cây con bên phải (LDR).
- Duyệt cây con bên trái, duyệt cây con bên phải và sau đó xử lý nút hiện tại (LRD).
- Xử lý nút hiện tại, duyệt cây con bên trái và sau đó duyệt cây con bên phải (DLR).
- Xử lý nút hiện tại, duyệt cây con bên phải và sau đó duyệt cây con bên trái (DRL).
- Duyệt cây con bên phải, xử lý nút hiện tại và sau đó duyệt cây con bên trái (RDL).
- Duyệt cây con bên phải, duyệt cây con bên trái và sau đó xử lý nút hiện tại (RLD).
Phân loại Duyệt cây
Phương pháp duyệt được sử dụng để xác định thứ tự xử lý các nút. Nếu chúng ta phân loại dựa trên nút hiện tại (D) và nếu D nằm ở giữa thì sự sắp xếp của L và R không quan trọng. Tương tự, vị trí của L và R cũng không quan trọng. Do đó, có tổng cộng 6 khả năng nhưng sau khi loại bỏ những khả năng trùng lặp, chỉ còn lại 3, đó là:
- Preorder (DLR) Traversal
- Inorder (LDR) Traversal
- Postorder (LRD) Traversal
Ngoài ra, còn có một phương pháp duyệt khác không phụ thuộc vào các đơn đặt hàng trên đó là Duyệt theo cấp độ (Level Order Traversal). Phương pháp này được lấy cảm hứng từ Breadth First Traversal của thuật toán Đồ thị.
Dưới đây là sơ đồ thể hiện các phương pháp duyệt cây:
Duyệt PreOrder
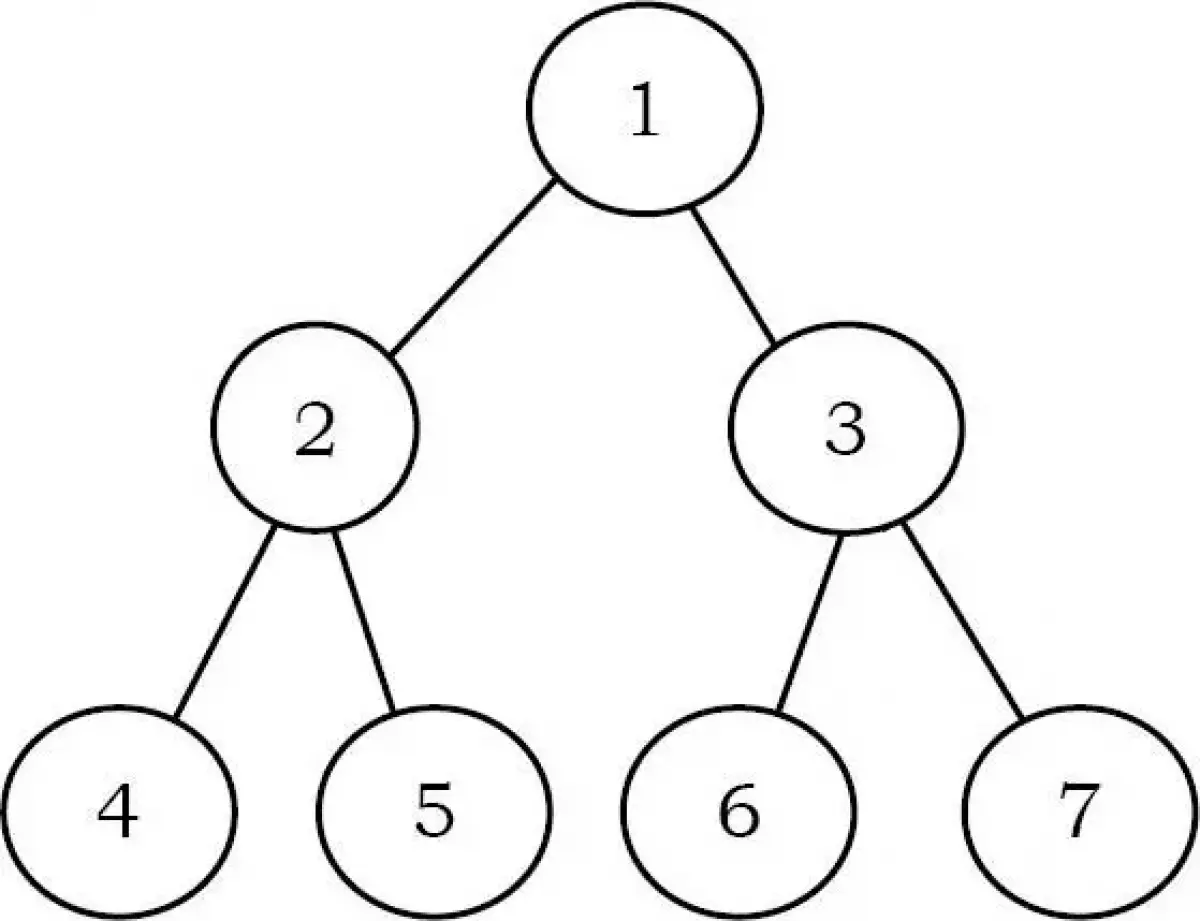
Trong Preorder Traversal, mỗi nút được xử lý trước (trước) một trong các cây con của nó. Đây là cách duyệt đơn giản nhất. Tuy nhiên, mặc dù mỗi nút được xử lý trước các cây con, nó vẫn yêu cầu một số thông tin phải được duy trì trong quá trình di chuyển xuống cây. Ví dụ: trong cây ở trên, số 1 được xử lý đầu tiên, sau đó là cây con bên trái và cuối cùng là cây con bên phải.
Do đó, để chuyển sang cây con bên phải sau khi xử lý cây con bên trái, chúng ta phải duy trì thông tin về gốc. Thông tin như vậy có thể được lưu trữ trong một ngăn xếp. Do cấu trúc LIFO của ngăn xếp, chúng ta có thể lấy lại thông tin về cây con bên phải theo thứ tự ngược lại.
Preorder Traversal được định nghĩa như sau:
- Ghé thăm gốc.
- Di chuyển qua cây con bên trái.
- Di chuyển qua cây con bên phải.
Các nút của cây sẽ được duyệt theo thứ tự: 1 2 4 5 3 6 7
public void preOrder(BinaryTreeNode root) {
if (root != null) {
System.out.println(root.data);
preOrder(root.left);
preOrder(root.right);
}
}Độ phức tạp thời gian: O(n). Độ phức tạp không gian: O(n).
Duyệt PreOrder theo vòng lặp
Trong phiên bản vòng lặp, chúng ta cần có một ngăn xếp để lưu trữ nút hiện tại, để khi hoàn thành xử lý cây con bên trái, chúng ta có thể chuyển sang cây con bên phải. Đầu tiên, chúng ta xử lý nút hiện tại và trước khi chuyển sang cây con bên trái, chúng ta lưu trữ nút hiện tại trên ngăn xếp. Sau khi hoàn thành xử lý cây con bên trái, chúng ta sẽ lấy phần tử trên đỉnh ngăn xếp và chuyển đến cây con bên phải của nó. Quá trình này được lặp lại cho đến khi ngăn xếp trống.
public ArrayList preOrderTraversal(BinaryTreeNode root) {
ArrayList res = new ArrayList<>();
if (root == null) {
return res;
}
Stack s = new Stack<>();
s.push(root);
while (!s.isEmpty()) {
BinaryTreeNode tmp = s.pop();
res.add(tmp.data);
if (tmp.right != null) {
s.push(tmp.right);
}
if (tmp.left != null) {
s.push(tmp.left);
}
}
return res;
} Duyệt InOrder
Trong Inorder Traversal, gốc được truy cập giữa việc duyệt các cây con. Duyệt Inorder được định nghĩa như sau:
- Di chuyển qua cây con bên trái trong Inorder.
- Ghé thăm gốc.
- Di chuyển qua cây con bên phải trong Inorder.
Các nút của cây sẽ được duyệt theo thứ tự: 4 2 5 1 6 3 7
public void inOrder(BinaryTreeNode root) {
if (root != null) {
inOrder(root.left);
System.out.println(root.data);
inOrder(root.right);
}
}Độ phức tạp thời gian: O(n). Độ phức tạp không gian: O(n).
Duyệt InOrder theo vòng lặp
Phiên bản không đệ quy của Duyệt InOrder tương tự như Duyệt PreOrder. Thay đổi duy nhất là thay vì xử lý nút trước khi chuyển đến cây con bên trái, chúng ta sẽ xử lý nút sau khi lấy phần tử trên đỉnh (được chỉ định sau khi hoàn thành xử lý cây con bên trái).
public ArrayList inOrderTraversal(BinaryTreeNode root) {
ArrayList res = new ArrayList<>();
Stack s = new Stack<>();
BinaryTreeNode currentNode = root;
boolean done = false;
while (!done) {
if (currentNode != null) {
s.push(currentNode);
currentNode = currentNode.left;
} else {
if (s.isEmpty()) {
done = true;
} else {
currentNode = s.pop();
}
res.add(currentNode.getData());
currentNode = currentNode.right;
}
}
return res;
} Duyệt PostOrder
Trong Duyệt PostOrder, gốc được truy cập sau khi duyệt qua cả hai cây con của nó. Duyệt PostOrder được định nghĩa như sau:
- Di chuyển qua cây con bên trái trong PostOrder.
- Di chuyển qua cây con bên phải trong PostOrder.
- Ghé thăm gốc.
Các nút của cây sẽ được duyệt theo thứ tự: 4 5 2 6 7 3 1
public void postOrder(BinaryTreeNode root) {
if (root != null) {
postOrder(root.left);
postOrder(root.right);
System.out.println(root.data);
}
}Độ phức tạp thời gian: O(n). Độ phức tạp không gian: O(n).
Duyệt PostOrder theo vòng lặp
Trong Duyệt PostOrder phiên bản không đệ quy, mỗi nút được truy cập hai lần. Sau khi xử lý cây con bên trái, chúng ta sẽ truy cập nút hiện tại và sau khi xử lý cây con bên phải, chúng ta sẽ truy cập nút hiện tại một lần nữa. Tuy nhiên, chúng ta chỉ xử lý nút trong lần truy cập thứ hai. Ở đây, vấn đề là làm thế nào để phân biệt xem chúng ta đang quay trở lại từ cây con bên trái hay cây con bên phải của nút hiện tại.
Chúng ta sử dụng một biến "previous" để theo dõi nút đã duyệt trước đó. Giả sử nút hiện tại nằm trên đỉnh của ngăn xếp. Khi "previous" là node cha của nút hiện tại, chúng ta đang đi xuống qua cây. Trong trường hợp này, chúng ta thử chuyển đến phần cây con bên trái của nút hiện tại nếu có (đẩy phần cây con bên trái vào ngăn xếp). Nếu không có, chúng ta xem xét phần cây con bên phải của nút hiện tại. Nếu cả cây con bên trái và cây con bên phải đều không tồn tại (nghĩa là nút hiện tại là một nút lá), chúng ta in giá trị của nút hiện tại và loại bỏ nó khỏi ngăn xếp.
public ArrayList postOrderTraversal(BinaryTreeNode root) {
ArrayList res = new ArrayList<>();
if (root == null) {
return res;
}
Stack s = new Stack<>();
s.push(root);
BinaryTreeNode prev = null;
while (!s.isEmpty()) {
BinaryTreeNode curr = s.peek();
if (prev == null || prev.left == curr || prev.right == curr) {
if (curr.left != null) {
s.push(curr.left);
} else if (curr.right != null) {
s.push(curr.right);
}
} else if (curr.left == prev) {
if (curr.right != null) {
s.push(curr.right);
}
} else {
res.add(curr.data);
s.pop();
}
prev = curr;
}
return res;
} Duyệt theo cấp độ
Duyệt theo cấp độ được định nghĩa như sau:
- Ghé thăm gốc.
- Trong khi duyệt qua level 1, giữ tất cả các phần tử ở level 1 trong hàng đợi.
- Chuyển đến level tiếp theo và duyệt qua tất cả các nút ở level đó.
- Lặp lại quá trình trên cho đến khi tất cả các level được duyệt qua.
Các nút của cây sẽ được duyệt theo thứ tự: 1 2 3 4 5 6 7
public ArrayList> levelOrder(BinaryTreeNode root) {
ArrayList> res = new ArrayList<>();
if (root == null) {
return res;
}
Queue q = new LinkedList<>();
q.offer(root);
q.offer(null);
ArrayList curr = new ArrayList<>();
while (!q.isEmpty()) {
BinaryTreeNode tmp = q.poll();
if (tmp != null) {
curr.add(tmp.data);
if (tmp.left != null) {
q.offer(tmp.left);
}
if (tmp.right != null) {
q.offer(tmp.right);
}
} else {
ArrayList c_curr = new ArrayList<>(curr);
res.add(c_curr);
curr.clear();
if (!q.isEmpty()) {
q.offer(null);
}
}
}
return res;
} Hy vọng qua bài viết này, các bạn đã hiểu về các phương pháp duyệt cây nhị phân và cách phân loại chúng thành các loại duyệt cụ thể.












