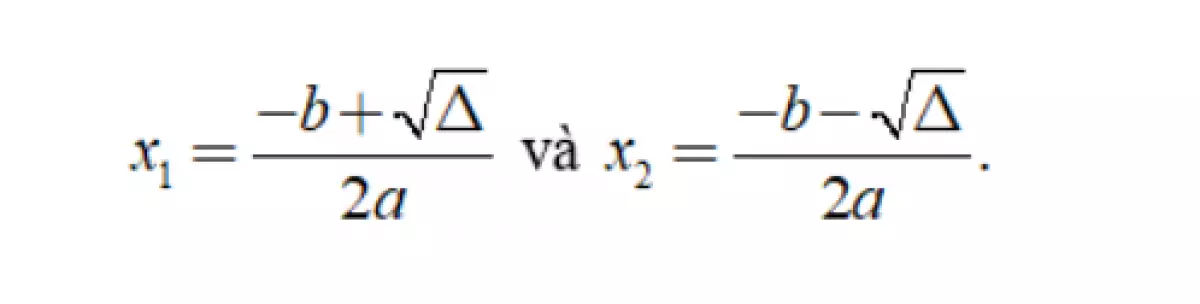
Introduction: Phương trình bậc 2 là một trong những chủ đề quan trọng trong môn Toán lớp 9. Việc hiểu và áp dụng công thức nghiệm của phương trình bậc 2 sẽ giúp chúng ta giải quyết dễ dàng các bài tập liên quan. Bài viết này sẽ giới thiệu về công thức nghiệm và trình bày các dạng bài tập thường gặp.
A. Lý thuyết về công thức nghiệm của phương trình bậc 2
1. Công thức nghiệm:
Đối với phương trình có dạng ax² + bx + c = 0 (a ≠ 0), ta có biệt thức của phương trình là: Δ = b² - 4ac.
-
Trường hợp 1: Nếu Δ > 0 thì ta có phương trình có 2 nghiệm phân biệt.
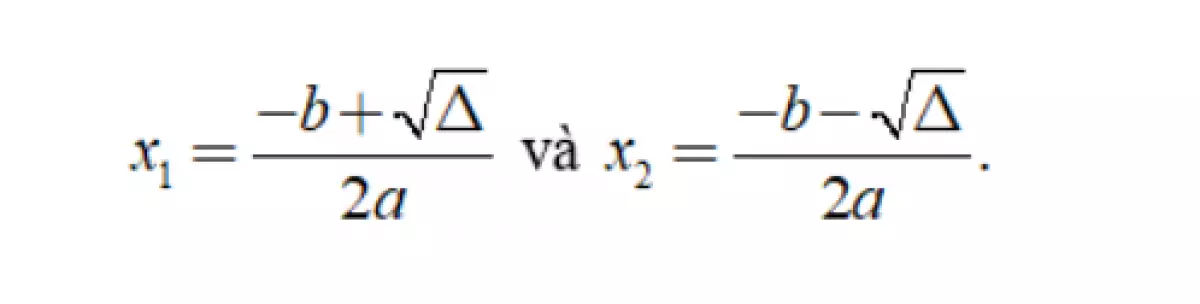
-
Trường hợp 2: Nếu Δ = 0 thì ta có phương trình có nghiệm kép.
-
Trường hợp 3: Nếu Δ < 0 thì ta có phương trình đã cho vô nghiệm.
2. Định lý Viet của phương trình bậc 2
Định lý Viet là một công thức quan trọng giúp chúng ta tìm mối liên hệ giữa các nghiệm và các ẩn của phương trình bậc 2. Theo định lý Viet, ta có:
- x1 + x2 = -b/a
- x1x2 = c/a
B. Dạng bài tập ứng dụng công thức nghiệm của phương trình bậc 2
Dạng bài tập 1: Phương trình bậc 2 1 ẩn không có tham số
Khi gặp dạng bài tập này, ta chỉ cần áp dụng công thức tính Δ và Δ' rồi sử dụng công thức tính nghiệm phương trình bậc 2 như đã được giới thiệu ở trên.
Ví dụ: Tìm nghiệm của phương trình sau: x² - 3x + 2 = 0.
Áp dụng công thức tính Δ, ta có Δ = b² - 4ac = 1.
Vậy nghiệm của phương trình trên lần lượt là:
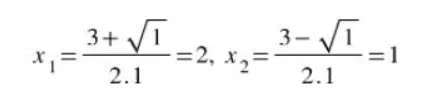
Dạng bài tập 2: phương trình bậc 2 có 1 ẩn là tham số
Bên cạnh dạng không chứa tham số, phương trình bậc 2 một ẩn có tham số cũng là một dạng bài tập quan trọng. Để giải dạng bài tập này, chúng ta cũng cần sử dụng công thức tính Δ và xét các trường hợp của Δ để đưa ra điều kiện như yêu cầu đề bài.
Các trường hợp của Δ bao gồm:
- Nếu Δ > 0 thì phương trình có 2 nghiệm phân biệt.
- Nếu Δ < 0 thì phương trình vô nghiệm.
- Nếu Δ = 0 thì phương trình có 1 nghiệm hoặc 2 nghiệm trùng nhau.
C. Các dạng bài thường gặp phương trình bậc 2
Hãy thử giải và làm các dạng bài tập sau để nắm vững kiến thức về công thức nghiệm của phương trình bậc 2.
-
Bài tập luyện tập:
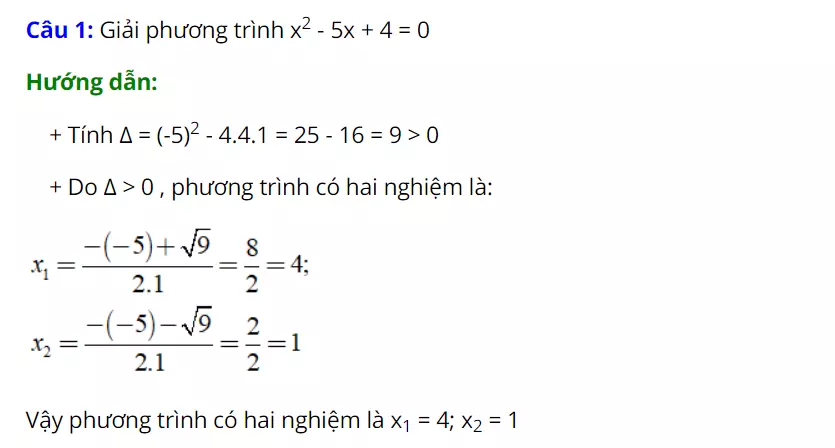
-
Bài tập thực hành: Hướng dẫn giải:

Hướng dẫn giải:

Tham khảo thêm các cách giải và phương pháp khác để làm bài về phương trình bậc 2.
Kết luận: Trên đây là những kiến thức cơ bản về công thức nghiệm của phương trình bậc 2 và các dạng bài tập thường gặp. Hy vọng rằng bài viết này đã giúp các em học sinh nắm được những kiến thức cần thiết để giải quyết các bài tập và chuẩn bị cho kỳ thi Toán vào lớp 10.












