Giới Thiệu
Bạn có bao giờ tự hỏi, liệu có cách nào để "ngược dòng" quá trình đạo hàm, từ đạo hàm của một hàm số, ta có thể tìm ra chính hàm số ban đầu? Câu trả lời nằm ở khái niệm nguyên hàm. Bài viết này sẽ dẫn dắt bạn đi từ những định nghĩa cơ bản nhất về nguyên hàm, đến các công thức thường gặp và các phương pháp giải bài tập hiệu quả.
Hãy tưởng tượng nguyên hàm như một chiếc chìa khóa vạn năng, mở ra cánh cửa để bạn giải quyết các bài toán trong toán học và nhiều lĩnh vực khác. Việc nắm vững kiến thức về nguyên hàm sẽ là nền tảng vững chắc cho bạn trong hành trình chinh phục toán học.
Nguyên Hàm là gì?
Nói một cách đơn giản, nguyên hàm của một hàm số f(x) là một hàm số F(x) có đạo hàm bằng chính f(x).
Ví dụ: Nguyên hàm của hàm số f(x) = 2x là F(x) = x² + C (với C là một hằng số bất kỳ).
Công Thức Nguyên Hàm Cơ Bản
Cũng giống như bảng cửu chương, nắm vững bảng công thức nguyên hàm cơ bản là bước đầu tiên để giải quyết các bài toán. Dưới đây là một số công thức thường gặp:


Phương Pháp Tìm Nguyên Hàm
Tìm nguyên hàm không chỉ đơn thuần là áp dụng công thức, mà còn đòi hỏi sự linh hoạt trong cách tư duy và lựa chọn phương pháp phù hợp.
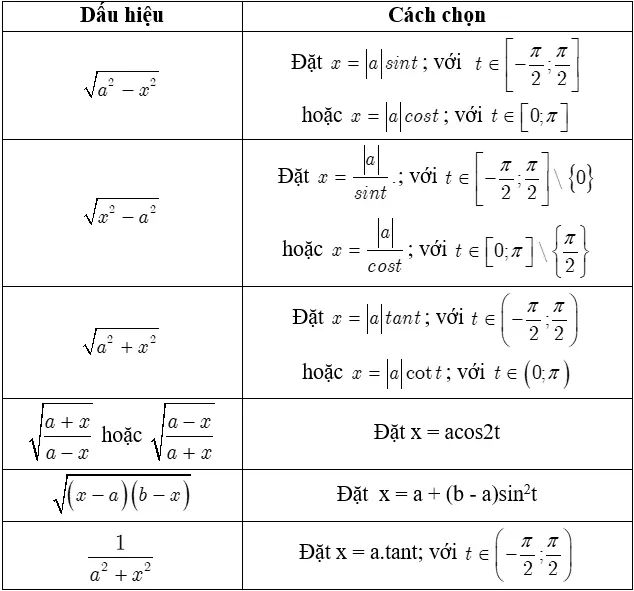
1. Phương pháp Đổi Biến
Phương pháp này giống như việc "thay áo mới" cho bài toán, biến đổi tích phân ban đầu thành một dạng đơn giản hơn.
2. Phương pháp Nguyên Hàm Từng Phần
Phương pháp nguyên hàm từng phần là "vũ khí bí mật" để giải quyết các bài toán phức tạp, bằng cách chia tích phân thành các phần nhỏ hơn.
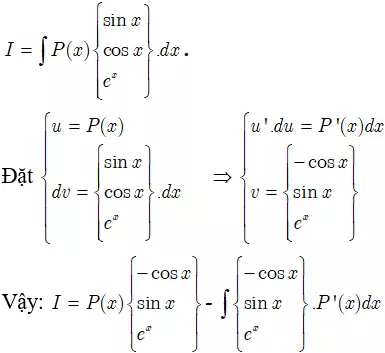
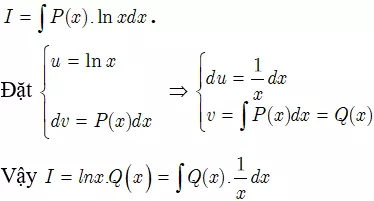
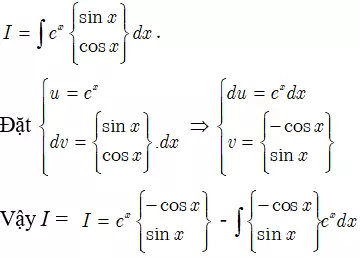
Lời Kết
Nguyên hàm là một khái niệm quan trọng trong toán học, mở ra cánh cửa để bạn khám phá những điều thú vị trong thế giới toán học và ứng dụng. Hy vọng bài viết này đã mang đến cho bạn cái nhìn tổng quan và những kiến thức bổ ích về nguyên hàm. Chúc bạn thành công trên con đường chinh phục toán học!












