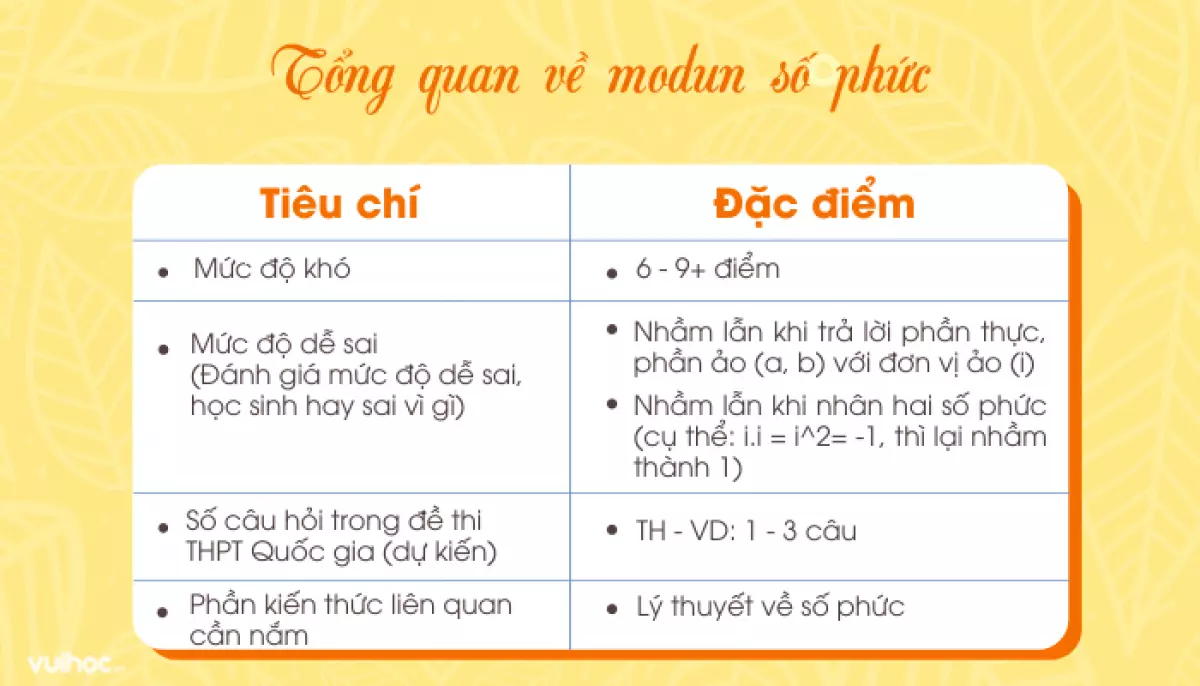
Trước khi bắt đầu, hãy cùng nhau nhìn vào bảng dưới đây để hiểu rõ hơn về mức độ khó và kiến thức cần ôn tập khi học về số phức modun!
Để giúp việc ôn tập và hiểu bài viết dễ dàng hơn, bạn có thể tải về tài liệu tổng hợp lý thuyết về modun, số phức modun dưới đây! Tài liệu này cũng rất hữu ích khi bạn ôn luyện đề thi đại học.
Tải xuống file tổng hợp lý thuyết về số phức modun
1. Lý thuyết về modun, modun của số phức
1.1. Modun của số phức là gì?
Modun của số phức $z=a+bi$ có thể được hiểu là độ dài của vectơ $u(a,b)$ biểu diễn số phức đó.
Theo một định nghĩa khác, modun của số phức $z=a+bi$ $(a,b \in \mathbb{R})$ là căn bậc hai số học (hay căn bậc hai không âm) của $a^2+b^2$. Ví dụ, số phức $3+4i$ có $3^2+4^2=25$ nên modun của $3+4i$ bằng 5. Chúng ta cũng dễ nhận thấy rằng trị tuyệt đối của một số thực cũng chính là modun của số thực đó. Do đó, đôi khi ta cũng gọi modun của số phức là giá trị tuyệt đối của số phức.

Mặt hình học, mỗi số phức $z=a+bi$ $(a,b \in \mathbb{R})$ được biểu diễn bởi một điểm $M(z)=(a;b)$ trên mặt phẳng $Oxy$ và ngược lại. Modun của $z$ được biểu diễn bởi độ dài đoạn thẳng $OM(z)$. Rõ ràng, modun của $z$ là một số thực không âm và nó chỉ bằng $0$ khi $z=0$.

1.2. Tính chất modun của số phức
Với modun của số phức, ta dễ dàng chứng minh được các tính chất sau:
(i) Hai số phức đối nhau có modun bằng nhau. Tức là $|z|=|-z|$.
(ii) Hai số phức liên hợp có modun bằng nhau. Tức là $|a+bi|=|a-bi|$.
(iii) Modun của $z$ bằng $0$ khi và chỉ khi $z=0$.
(iv) Tích của hai số phức liên hợp bằng bình phương modun của chúng.

(v) Modun của một tích bằng tích các modun.

(vi) Modun của một thương bằng thương các modun.

1.3. Bất đẳng thức modun của số phức
Vì modun của số phức là độ dài đoạn thẳng trong mặt phẳng, từ các bất đẳng thức tam giác ta có thể suy ra các bất đẳng thức về modun của số phức tương tự.
Tổng hai cạnh trong một tam giác luôn lớn hơn cạnh thứ ba. Từ đó ta có bất đẳng thức:

Dấu bằng xảy ra khi:

Cũng từ bất đẳng thức tam giác nêu trên, ta có thể suy ra được các bất đẳng thức sau:

Dấu bằng xảy ra khi:

Vì modun của số phức mang lại nhiều điểm thú vị và tính chất thú vị, hãy tiếp tục khám phá để bạn hiểu rõ hơn về nó!
2. Phương pháp giải bài tập tính modun của số phức
2.1. Phương pháp tính modun của số phức
Để giải các bài tập tính modun của số phức, bạn cần nắm vững công thức sau để giải bài tập:

Kết quả: $\forall z \in \mathbb{C}$ ta có:

2.2. Ví dụ minh hoạ
Hãy xem qua các ví dụ minh hoạ về bài tập tính modun của số phức dưới đây để hiểu rõ hơn về cách làm và áp dụng công thức biến đổi modun của số phức!




3. Bài tập luyện tập số phức modun
Thực hành các bài tập số phức modun là cách tốt nhất để hiểu sâu về lý thuyết và trở nên thành thạo khi gặp các bài tập liên quan trong các đề thi. Dưới đây là một số dạng bài tập số phức modun mà bạn có thể sử dụng để luyện tập thêm!
Bài viết đã tổng hợp tất cả lý thuyết và các dạng bài tập thường gặp khi ôn tập về số phức modun. Chúc bạn học tập tốt!
>> Xem thêm:












