Lời mở đầu
Chào bạn, đã bao giờ bạn tự hỏi làm thế nào để giải quyết những bài toán hóc búa liên quan đến hai đại lượng chưa biết? Đừng lo lắng, bài viết này sẽ giúp bạn "giải mã" bí ẩn đó! Chúng ta sẽ cùng nhau khám phá thế giới của hệ phương trình bậc nhất hai ẩn, một chủ đề thú vị trong chương trình Toán 9.
Đừng lo lắng nếu bạn cảm thấy "ngợp" bởi những thuật ngữ toán học khô khan! Bài viết này được viết với ngôn ngữ gần gũi, dễ hiểu như một cuộc trò chuyện giữa những người bạn. Chúng ta sẽ cùng tìm hiểu ba phương pháp giải hệ phương trình: phương pháp thế, phương pháp cộng đại số và sử dụng máy tính. Bên cạnh đó, bạn còn được "thực hành" với một số bài tập ví dụ và khám phá cách ứng dụng hệ phương trình vào giải quyết các vấn đề thực tế.
Sẵn sàng chưa? Cùng bắt đầu hành trình khám phá nào!
Phương pháp thế: "Hô biến" ẩn số
Giống như trò ảo thuật, phương pháp thế giúp ta "hô biến" một ẩn số, biến bài toán hai ẩn thành bài toán một ẩn đơn giản hơn.
Các bước thực hiện:
-
Bước 1: Chọn một trong hai phương trình của hệ, biểu diễn một ẩn theo ẩn còn lại. Ví dụ, từ phương trình
x + y = 5, ta có thể biểu diễnx = 5 - y. -
Bước 2: Thế biểu thức vừa tìm được vào phương trình còn lại của hệ. Lúc này, ta sẽ có một phương trình chỉ chứa một ẩn duy nhất.
-
Bước 3: Giải phương trình một ẩn vừa thu được để tìm giá trị của ẩn đó.
-
Bước 4: Thế giá trị của ẩn đã tìm được ở bước 3 vào một trong hai phương trình ban đầu để tìm giá trị của ẩn còn lại.
Phương pháp cộng đại số: "Kết hợp" để loại bỏ
Phương pháp cộng đại số tận dụng sự linh hoạt trong phép toán cộng trừ để loại bỏ một ẩn, từ đó tìm ra lời giải cho bài toán.
Các bước thực hiện:
-
Bước 1: Quan sát hệ số của hai ẩn trong hai phương trình. Nếu hệ số của cùng một ẩn trong hai phương trình bằng nhau hoặc đối nhau, ta có thể chuyển sang bước tiếp theo.
-
Bước 2: Cộng hoặc trừ từng vế của hai phương trình trong hệ để triệt tiêu một ẩn.
-
Bước 3: Giải phương trình một ẩn vừa nhận được.
-
Bước 4: Thay giá trị của ẩn đã tìm được ở bước 3 vào một trong hai phương trình ban đầu để tìm giá trị của ẩn còn lại.
"Siêu trợ thủ" máy tính cầm tay
Ngày nay, máy tính cầm tay đã trở thành một "siêu trợ thủ" đắc lực giúp chúng ta giải quyết các bài toán một cách nhanh chóng và chính xác, bao gồm cả việc giải hệ phương trình bậc nhất hai ẩn.
Các bước thực hiện:
-
Bước 1: Chuyển hệ phương trình về dạng chuẩn:
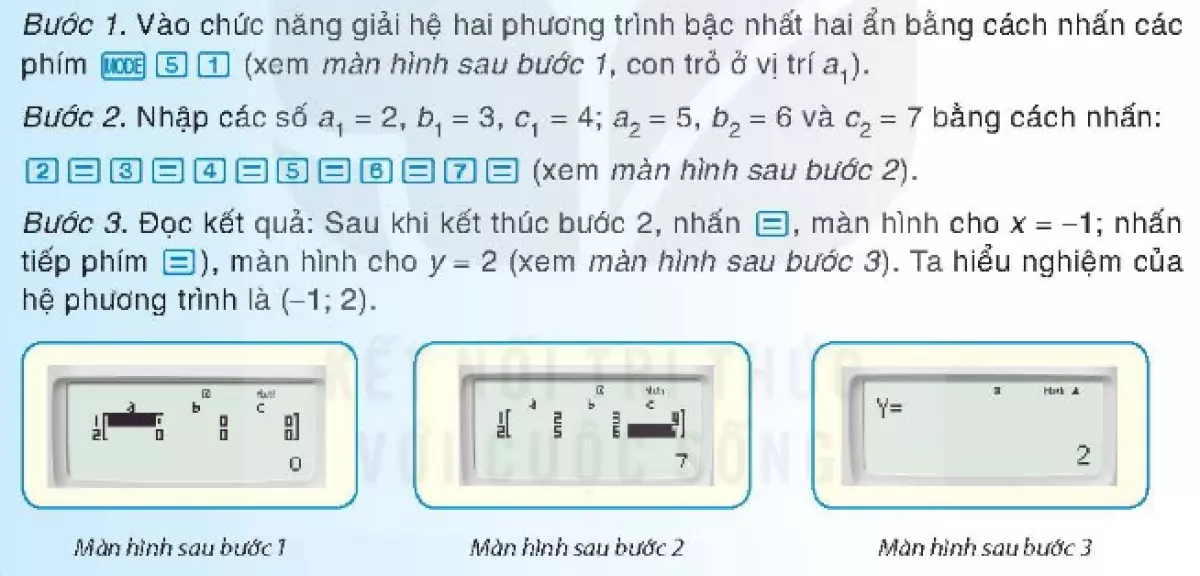
Công thức phương trình bậc nhất -
Bước 2: Sử dụng chức năng giải hệ phương trình trên máy tính (thường là phím MODE).
-
Bước 3: Nhập các hệ số của hệ phương trình vào máy tính theo thứ tự a1, b1, c1, a2, b2, c2.
-
Bước 4: Nhấn dấu "=" để nhận kết quả là nghiệm của hệ phương trình.
Giải bài toán bằng cách lập hệ phương trình: Từ lý thuyết đến thực tiễn
Hệ phương trình bậc nhất hai ẩn không chỉ là một khái niệm toán học trừu tượng mà còn có rất nhiều ứng dụng thực tiễn. Ta có thể sử dụng hệ phương trình để giải quyết các bài toán liên quan đến tuổi tác, vận tốc, tỉ lệ...
Các bước thực hiện:
-
Bước 1: Lập hệ phương trình:
- Xác định hai đại lượng chưa biết và đặt ẩn cho chúng.
- Biểu diễn các đại lượng liên quan theo ẩn và các đại lượng đã biết.
- Lập hai phương trình bậc nhất hai ẩn dựa trên các mối quan hệ đã cho trong bài toán.
-
Bước 2: Giải hệ phương trình vừa lập để tìm giá trị của hai ẩn.
-
Bước 3: Kiểm tra xem nghiệm tìm được có thỏa mãn điều kiện của bài toán hay không và kết luận.
Luyện tập cùng bài tập
Để "nâng cao trình độ" và tự tin hơn với hệ phương trình bậc nhất hai ẩn, hãy cùng thử sức với một số bài tập sau đây nhé!
Bài 1: Giải hệ phương trình sau bằng phương pháp thế:

Bài 2: Giải hệ phương trình sau bằng phương pháp cộng đại số:
Bài 3: Một cửa hàng bán 2 loại bánh: bánh ngọt và bánh mặn. Biết rằng giá 1 cái bánh ngọt là 5.000 đồng, giá 1 cái bánh mặn là 3.000 đồng. Hôm nay, cửa hàng bán được tổng cộng 100 cái bánh và thu về 380.000 đồng. Hỏi cửa hàng đã bán được bao nhiêu cái bánh mỗi loại?
Kết thúc hành trình
Chúc mừng bạn đã hoàn thành hành trình khám phá thế giới phương trình bậc nhất hai ẩn!
Như bạn đã thấy, hệ phương trình không hề "đáng sợ" như bạn nghĩ, phải không nào? Bằng cách nắm vững lý thuyết, thành thạo các phương pháp giải và chăm chỉ luyện tập, bạn hoàn toàn có thể "chinh phục" mọi bài toán liên quan đến hệ phương trình. Hãy nhớ rằng, toán học không chỉ là những con số khô khan mà còn là chìa khóa mở ra thế giới xung quanh chúng ta!












