Hình ảnh minh họa - Hai mặt phẳng vuông góc
Định nghĩa hai mặt phẳng vuông góc
Hai mặt phẳng vuông góc là khi hai mặt phẳng tạo thành một góc vuông, tức là góc giữa chúng là 90 độ.
Điều kiện để hai mặt phẳng vuông góc
Hai mặt phẳng vuông góc với nhau khi và chỉ khi một mặt phẳng chứa đường thẳng vuông góc với mặt phẳng còn lại.
Các tính chất của hai mặt phẳng vuông góc là:
-
Nếu hai mặt phẳng vuông góc với nhau, bất kỳ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ cũng vuông góc với mặt phẳng kia.
-
Nếu hai mặt phẳng (A) và (B) vuông góc với nhau, một đường thẳng a qua điểm H (với điểm H nằm trên mặt phẳng A) và vuông góc với (B) sẽ nằm trong (A).
-
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba, thì giao tuyến của chúng sẽ vuông góc với mặt phẳng còn lại.
Hai mặt phẳng vuông góc trong tọa độ không gian Oxyz
Phương trình tổng quát của mặt phẳng (P) trong không gian tọa độ Oxyz có dạng tổng quát như sau:
Ax + By + Cz + D = 0với A^2 + B^2 + C^2 > 0
Để viết phương trình mặt phẳng trong không gian, ta cần xác định 2 điều kiện:
- Điểm M nằm trên mặt phẳng.
- Vector pháp tuyến của mặt phẳng.
Đăng ký ngay để được các thầy cô tư vấn và xây dựng lộ trình ôn thi THPT môn Toán sớm ngay từ bây giờ.
Hình ảnh minh họa - Hai mặt phẳng vuông góc trong tọa độ không gian Oxyz
Điều kiện để hai mặt phẳng vuông góc trong không gian tọa độ Oxyz
Cho 2 mặt phẳng có phương trình lần lượt là:
(P): Ax + By + Cz + D = 0 (Q): A'x + B'y + C'z + D' = 0.
Điều kiện để hai mặt phẳng vuông góc với nhau khi và chỉ khi thỏa mãn điều kiện: AA' + BB' + CC' + DD' = 0.
Phương pháp chứng minh hai mặt phẳng vuông góc
Phương pháp chứng minh 2 mặt phẳng vuông góc với nhau
Cách 1: Chứng minh mặt phẳng này chứa đường thẳng d vuông góc với mặt phẳng còn lại.
Cách 2: Chứng minh góc giữa hai mặt phẳng là 90 độ.
Phương pháp chứng minh đường thẳng d vuông góc với mặt phẳng (α)
Cách 1: Nếu hai mặt phẳng cho trước cùng vuông góc với mặt phẳng thứ ba, thì giao tuyến (nếu có) của chúng cũng sẽ vuông góc với mặt phẳng này.
Cách 2: Nếu hai mặt phẳng vuông góc với nhau, nếu có một đường thẳng nằm trong mặt phẳng này vuông góc với giao tuyến của hai mặt phẳng, thì nó cũng vuông góc với mặt phẳng còn lại.
Kết quả:
- S' = S * cos(φ)
- Nếu hai mặt phẳng (Q) và (P) vuông góc với nhau, một điểm A bất kỳ thuộc mặt phẳng (P), thì mọi đường thẳng qua điểm A và vuông góc với mặt phẳng (Q) đều nằm trong mặt phẳng (P).
Tham khảo ngay bộ tài liệu nắm trọn kiến thức và phương pháp giải mọi dạng bài tập độc quyền của VUIHOC.
Hình ảnh minh họa - Hai mặt phẳng vuông góc
Bài tập hai mặt phẳng vuông góc cơ bản
Bài tập tự luận
Bài tập 1: Cho hình chóp SABC có đáy là tam giác vuông ABC, góc B bằng 90 độ. Gọi 2 điểm H, K lần lượt là các hình chiếu vuông góc của A trên 2 đoạn thẳng SB, SC. Hãy chứng minh: mặt phẳng (SAB) vuông góc với mặt phẳng (SBC), mặt phẳng (AHK) vuông góc với mặt phẳng (SBC).
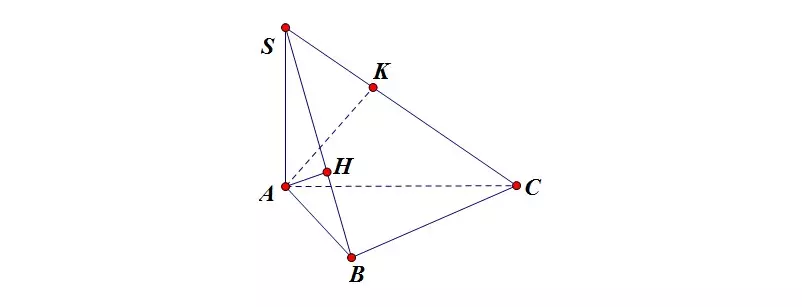
Hướng dẫn phương pháp giải:
Chứng minh mặt phẳng (SAB) vuông góc với mặt phẳng (SBC):
Để chứng minh hai mặt phẳng vuông góc với nhau, ta cần chứng minh trong mặt phẳng này có 1 đường thẳng vuông góc với mặt phẳng kia.
Ta có: Tam giác ABC vuông tại B. Suy ra: AB ⊥ BC (1)
SA ⊥ (ABC) ⇒ SA ⊥ BC (2)
Từ (1) và (2) ta suy ra được:
⇒ BC ⊥ (SAB), BC ⊂ (SBC) ⇒ (SAB) ⊥ (SBC) (điều phải chứng minh)
Chứng minh mặt phẳng (AHK) vuông góc với mặt phẳng (SBC)
Ta có:
BC ⊥ (SAB) mà AH thuộc mặt phẳng (SAB) ⇒ BC ⊥ AH(3)
H là hình chiếu vuông góc của A (theo giả thuyết)
⇒ SB ⊥ AH(4)
Từ (3) và (4) ta suy ra được
AH ⊥ (SBC) mà AH ⊂ (AHK) ⇒ (AHK) ⊥ (SBC) (điều phải chứng minh)
Bài tập 2: Cho hai mặt phẳng Δ và (β) vuông góc với nhau và cắt nhau thông qua giao tuyến d. Hãy chứng minh nếu có một đường thẳng Δ nằm trong Δ và Δ vuông góc với giao tuyến d thì Δ vuông góc với mặt phẳng (β).
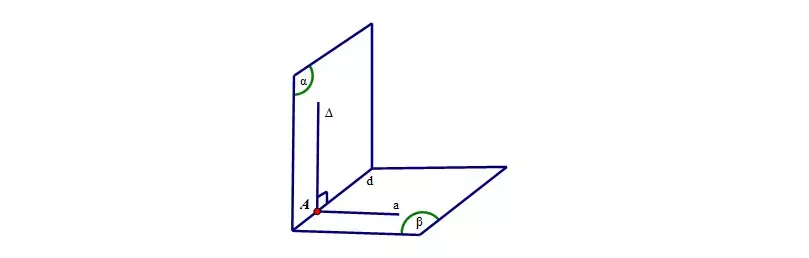
Hướng dẫn phương pháp giải:
Ta có:
Từ điểm A, ta kẻ đường thẳng a:
Do
hay
