Trong chương trình học cấp ba, hàm số là kiến thức cơ bản và nền tảng giúp chúng ta có thể giải quyết nhiều bài tập từ cơ bản đến nâng cao. Vì vậy, hàm số đã được đưa vào chương trình học lớp 10. Nhưng hàm số lớp 10 là gì? Làm thế nào để biểu diễn qua đồ thị hàm số? Hãy cùng tôi ôn tập lại các kiến thức cơ bản cũng như các dạng bài tập từ cơ bản đến nâng cao về hàm số.
Kiến thức cần nắm được
- Hiểu khái niệm về hàm số, tập xác định, đồ thị hàm số, tính chẵn lẻ của hàm số, và cách vẽ đồ thị hàm số.
- Áp dụng định nghĩa để giải các bài tập liên quan đến hàm số.
- Biết cách biểu diễn và vẽ đồ thị hàm số lớp 10.
Cơ sở lý thuyết cần nắm
Thế nào là hàm số lớp 10?
Hàm số lớp 10 là một quy luật xác định mỗi số thực x trong tập xác định có một số thực y tương ứng trong tập giá trị. Đồ thị hàm số trên hệ trục tọa độ tạo thành một dạng đường cong nhất định. Để biểu diễn đồ thị hàm số, ta thường sử dụng bảng giá trị và bút vẽ đồ thị.
Định nghĩa về đồ thị hàm số
Đồ thị hàm số là một biểu diễn đồ họa của một hàm số trên hệ trục tọa độ. Đồ thị này thường được vẽ trên mặt phẳng Oxy, trong đó trục hoành OX là trục xác định, và trục tung OY là trục giá trị. Mỗi điểm trên đồ thị hàm số tương ứng với một cặp giá trị (x, y) của hàm số.
Sự biến thiên của hàm số được định nghĩa ra sao?
Sự biến thiên của hàm số được xác định bằng cách xem xét độ dốc của đồ thị hàm số tại mỗi điểm. Hàm số có thể có các sự biến thiên khác nhau: tăng, giảm, bằng 0, hay không biến thiên. Sự biến thiên này sẽ được thể hiện dựa trên đồ thị hàm số.
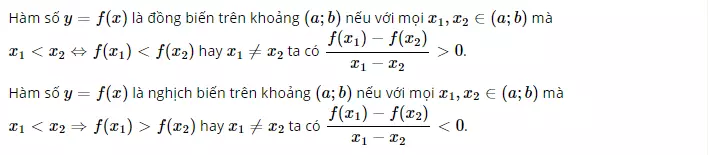
Tính chẵn lẻ của hàm số
Một hàm số được gọi là chẵn nếu đồ thị hàm số đối xứng qua trục tung. Nghĩa là, nếu (x, y) là một điểm trên đồ thị hàm số, thì điểm (-x, y) cũng sẽ nằm trên đồ thị. Một hàm số được gọi là lẻ nếu đồ thị hàm số đối xứng qua gốc tọa độ. Nghĩa là, nếu (x, y) là một điểm trên đồ thị hàm số, thì điểm (-x, -y) cũng sẽ nằm trên đồ thị.
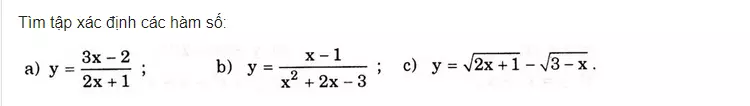
Xem thêm: Hàm số và những kiến thức cơ bản - Toán lớp 7 là chuyện nhỏ
Các dạng bài tập về hàm số lớp 10
Dạng 1: Cho 1 hàm số, hãy tính giá trị của hàm số đó tại 1 điểm xác định
Cách giải dạng bài toán này như sau: Cho hàm số y = f(x) tại x = a. Để tính giá trị của hàm số đã cho tại điểm a, ta thay x = a vào biểu thức của hàm số và tính được f(a).
Ví dụ: Cho hàm số: y = f(x) = 5x^2 + 3x - 2.
Hãy tính giá trị của biểu thức f(-2) và f(2).
Giải:
Ta có: f(-2) = 5(-2)^2 + 3(-2) - 2 = 12
f(2) = 5(2)^2 + 3(2) - 2 = 24
Dạng 2: Hãy tìm tập xác định của hàm số
Dạng bài toán này xuất hiện trong tất cả các chương trình học THPT và giúp ta có thể giải phương trình hay bất phương trình. Vì vậy, ta cần nắm vững kiến thức để có thể xử lý được các dạng bài tập.
Cách giải bài toán này như sau: Cho hàm số y = f(x), hãy tìm tập xác định của hàm số đã cho sao cho hàm số f(x) có nghĩa.
Ví dụ: Hãy tìm tập xác định của các hàm số sau:
- a)
y = 5x / (2x-1)Giải: Hàm số trên xác định khi2x-1 ≠ 0 ⇔ x ≠ 1/2 - b)
y = √(x^2-3x)Giải: Hàm số trên xác định khix^2 - 3x ≠ 0 ⇔ x(x - 3) ≠ 0 ⇔ x ≠ 0 và x ≠ 3.
Dạng 3: Xác định tính chẵn lẻ của hàm số đã cho
Cách giải bài toán này như sau:
- Tập
Dlà tập đối xứng. - Tính giá trị hàm số
f(-x)- Nếu hàm số
f(-x) = f(x)thì hàm số đó là hàm số chẵn. - Nếu hàm số
f(-x) = -f(x)thì đây là hàm số lẻ.
- Nếu hàm số
- Đồ thị của hàm số chẵn sẽ nhận trục tung làm trục đối xứng.
- Đồ thị của hàm số lẻ sẽ nhận gốc tọa độ làm tâm đối xứng.
Ví dụ: Xác định tính chẵn lẻ của các hàm số sau:
- a)
y = -2x^2 + 3Giải: Ta cóD = Rf(-x) = -2(-x)^2 + 3 = -2x^2 + 3 = f(x) => y là hàm số chẵn - b)
y = 1 /(2x)Ta cóD = R{0}f(-x) = 1 / (2. (-x)) = -(1/2x) = -f(x)=> y là hàm số lẻ.
Giải bài tập toán 10 hàm số - SGK
Bài 1: SGK - 38
Hướng dẫn giải bài tập:
a) Hàm số y = f(x)
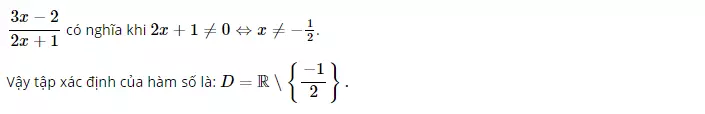b)
c)
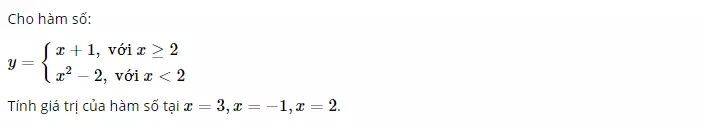
Bài 2: SGK - 38
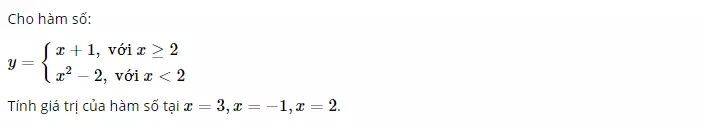Giải bài toán:
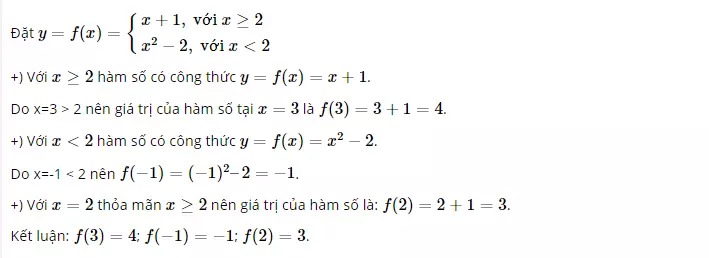
Bài 3: SGK - 39
Cách giải bài toán:
Giải bài toán:
a) M(-1; 6)
Đồ thị hàm số y = 3x^3 - 2x + 1 xác định khi D = R
Thay x=-1 ta có hàm số y = 3.(-1)^2 - 2.(-1) + 1 = 6
Vậy điểm M(-1; 6) thuộc đồ thị hàm số y = 3x^3 - 2x + 1
b) N(1;1)
Thay x = 1 vào hàm số y = 3.1^2 - 2.1 + 1 = 2 ≠ 1
=> Điểm N(1; 1) không thuộc đồ thị hàm số trên.
c) P(0; 1)
Tương tự như cách giải phần a) và b)
Ta thay x = 0 vào hàm số đã cho. Ta có:
y = 3. 0^2 - 2.0 + 1 = 1 => Điểm P(0; 1) thuộc đồ thị hàm số đã cho.
Bài 4: SGK - 39
Giải bài toán:
a) Hãy tìm m sao cho điểm O(-1; 3) thuộc đồ thị trên.
b) Tìm các điểm cố định mà đồ thị hàm số cho luôn đi qua với mọi giá trị điểm m.
Giải bài tập nâng cao
Hãy rèn luyện thêm cho bản thân bằng cách làm các bài tập từ cơ bản đến nâng cao. Hãy dùng toàn bộ những kiến thức đã ôn tập ở trên để giải các bài toán dưới đây:
Bài 1: Vận dụng các kiến thức đã học, hãy xác định các hàm số sau:
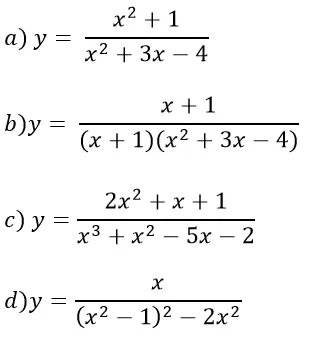
Bài 2: Cho các hàm số dưới đây, hãy xét tính chẵn lẻ của hàm số lớp 10:
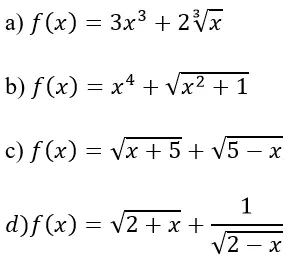
Bài 3: Cho hàm số y = 2x^2 + 5
a) Hãy xét chiều biến thiên của hàm số đã cho trên (-∞; 0) và (0; +∞).
b) Hãy lập bảng biểu diễn chiều biến thiên của hàm số lớp 10 trên [-2; 1]. Từ đây, xác định GTLN và GTNN của hàm số.
Bài 4: Cho hàm số: y = - mx^3 + 3(m^2 - 1)x^2 + 4mx - 5m
a) Hãy tìm m sao cho điểm O(-1; 3) thuộc đồ thị trên.
b) Tìm các điểm cố định mà đồ thị hàm số cho luôn đi qua với mọi giá trị điểm m.
Tổng kết kiến thức vừa ôn tập
Trên đây là lý thuyết và các dạng bài tập về hàm số lớp 10 mà chúng ta đã ôn tập. Hy vọng qua những bài tập trên, các bạn có thể rút ra được cho bản thân những kiến thức cơ bản. Từ đó, có thể dễ dàng áp dụng một cách linh hoạt vào giải các bài toán khó hơn. Hy vọng đây là nguồn chia sẻ, trau dồi kiến thức cho các bạn thật tốt, giúp các bạn có được thành tích cao trong học tập.
