Dạng lượng giác của số phức: Cho số phức z có dạng $z = r\left( {\cos \varphi + i\sin \varphi } \right)$ thì ta luôn có: ${z^n} = {r^n}\left( {\cos n\varphi + i\sin n\varphi } \right)$.
Giới thiệu
Trong toán học, giải phương trình số phức là một phần quan trọng và phức tạp. Tuy nhiên, với sự trợ giúp của máy tính và phương pháp Casio, việc giải hệ phương trình số phức đã trở nên dễ dàng hơn bao giờ hết.
Định nghĩa
Hệ phương trình số phức là một tập hợp các phương trình có dạng ${z^2} - z + 1 = 0$ hay ${z^2} + 2z + 2 = 0$ và phải tìm nghiệm phức ${z_1},{z_2}$ của hệ phương trình đó.
Ví dụ minh họa
VD1. (Thi thử chuyên Khoa học tự nhiên lần 1) Gọi ${z_1},{z_2}$ là hai nghiệm phức của phương trình ${z^2} - z + 1 = 0$. Giá trị của $|{z_1}| + |{z_2}|$ bằng: A.0 B.1 C.2 D.4
Lời giải: Tính nghiệm của phương trình bậc hai ${z^2} - z + 1 = 0$ bằng chức năng MODE 5 3.
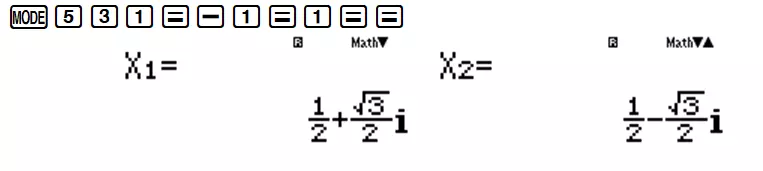
Vậy ta được hai nghiệm ${z_1} = \frac{1}{2} + \frac{\sqrt{3}}{2}i$ và ${z_2} = \frac{1}{2} - \frac{\sqrt{3}}{2}i$. Tính tổng Môđun của hai số phức trên ta lại dùng chức năng SHIFT HYP.
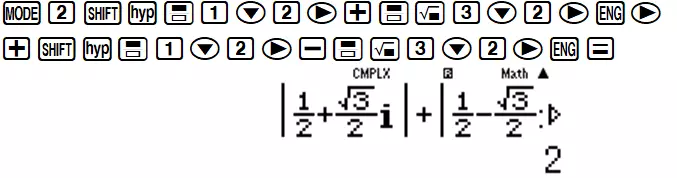
$\Rightarrow |{z_1}| + |{z_2}| = 2$ ta thấy B là đáp án chính xác.
VD2. (Thi thử chuyên Khoa học tự nhiên lần 2) Gọi ${z_1},{z_2}$ là hai nghiệm phức của phương trình ${z^2} + 2z + 2 = 0$. Tính giá trị của biểu thức $P = {z_1}^{2016} + {z_2}^{2016}$: A. ${2^{1009}}$ B.0 C. ${2^{2017}}$ D. ${2^{1008}}$
Lời giải: Tính nghiệm của phương trình bậc hai ${z^2} + 2z + 2 = 0$ bằng chức năng MODE 5 3.

Ta thu được hai nghiệm ${z_1} = - 1 + i$ và ${z_2} = - 1 - i$. Với các cụm đặc biệt -1+i, -1-i ta có điều đặc biệt sau: ${(-1 + i)^4} = - 4$, ${(-1 - i)^4} = - 4$.

Vậy $P = {z_1}^{2016} + {z_2}^{2016} = {(-1 + i)^{2016}} + {(-1 - i)^{2016}} = {\left( {-4} \right)^{504}} + {\left( {-4} \right)^{504}} = {4^{504}} + {4^{504}} = {2^{1008}} + {2^{1008}} = {2 \cdot 2^{1008}} = {2^{1009}}$. $P = {z_1}^{2016} + {z_2}^{2016} = {2^{1009}}$ ta thấy A là đáp án chính xác.
VD3. (Đề minh họa bộ GD-ĐT lần 1) Kí hiệu ${z_1},{z_2},{z_3}$ và ${z_4}$ là bốn nghiệm phức của phương trình ${z^4} - {z^2} - 12 = 0$. Tính tổng: $T = |{z_1}| + |{z_2}| + |{z_3}| + |{z_4}|$ A. T = 4 B. $T = 2\sqrt{3}$ C. $T = 4 + 2\sqrt{3}$ D. $T = 2 + 2\sqrt{3}$
Lời giải: Để tính nghiệm của phương trình ta dùng chức năng MODE 5. Tuy nhiên máy tính chỉ tính được phương trình bậc 2 và 3 nên để tính được phương trình bậc 4 trùng phương ${z^4} - {z^2} - 12 = 0$ thì ta coi ${z^2} = t$ khi đó phương trình trở thành ${t^2} - t - 12 = 0$.

Vậy $\left{ \begin{array}{l} t = 4 \ t = -3 \end{array} \right.$ hay $\left{ \begin{array}{l} {z^2} = 4 \ {z^2} = -3 \end{array} \right.$ Với ${z^2} = 4 \Rightarrow z = \pm 2$ Với ${z^2} = -3$ ta có thể đưa về ${z^2} = 3i^2 \Leftrightarrow z = \pm \sqrt{3}i$ với ${i^2} = -1$. Hoặc ta có thể tiếp tục sử dụng chức năng MODE 5 cho phương trình ${z^2} = -3 \Leftrightarrow {z^2} + 3 = 0$.
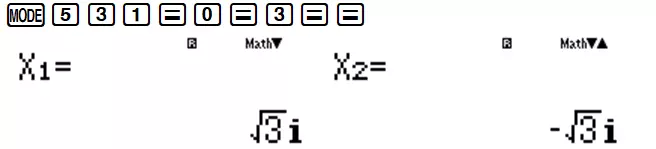
Tóm lại ta sẽ có 4 nghiệm $z = \pm 1,\,\,\,z = \pm \sqrt{3}i$. Tính T ta lại sử dụng chức năng tính môđun SHIFT HYP.
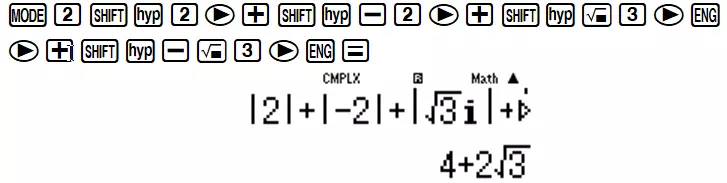
VD4: (Thi thử nhóm toán Đoàn Trí Dũng lần 3) Giải phương trình sau trên tập số phức: ${z^3} + (i + 1){z^2} + (i + 1)z + i = 0$ A. $z=-i$ B. $z = - \frac{1}{2} + \frac{\sqrt{3}}{2}i$ C. $z = - \frac{1}{2} - \frac{\sqrt{3}}{2}i$ D. Cả A, B, C đều đúng
Lời giải: Để kiểm tra nghiệm của 1 phương trình ta sử dụng chức năng CALC.

Vậy $z=-i$ là nghiệm. Tiếp tục kiểm tra $z = - \frac{1}{2} + \frac{\sqrt{3}}{2}i$ nếu giá trị này là nghiệm thì cả đáp án A và B đều đúng có nghĩa là đáp án D chính xác. Nếu giá trị này không là nghiệm thì chỉ có đáp án A đúng duy nhất.
Đáp án chính xác là D.
VD5: (Thi thử báo Toán học tuổi trẻ lần 3) Trong các phương trình dưới đây, phương trình nào có hai nghiệm ${z_1} = 1 + \sqrt{3} ,\;{z_2} = 1 - \sqrt{3}$ A. ${z^2} + i\sqrt{3}z + 1 = 0$ B. ${z^2} + 2\sqrt{3}z + 4 = 0$ C. ${z^2} - 2\sqrt{3}z + 4 = 0$ D. ${z^2} - 2\sqrt{3}z - 4 = 0$
Lời giải: Ta hiểu phương trình bậc hai $a{x^2} + bx + c = 0$ nếu có hai nghiệm thì sẽ tuân theo định lý Vi-et (kể cả trên tập số thực hay tập số phức): $\left{ \begin{array}{l} {z_1} + {z_2} = - \frac{b}{a} \ {z_1}{z_2} = \frac{c}{a} \end{array} \right.$ Tính ${z_1} + {z_2} = 2$
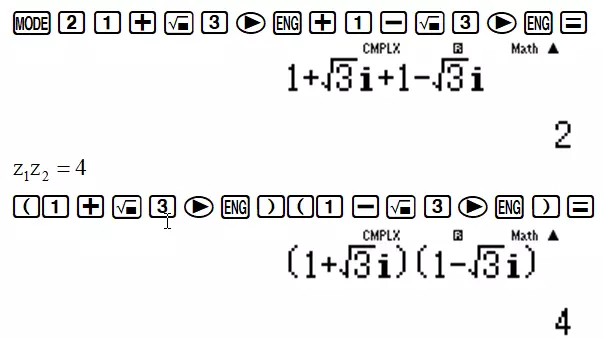
Rõ ràng chỉ có phương trình ${z^2} - 2\sqrt{3}z + 4 = 0$ có $ - \frac{b}{a} = 2$ và $\frac{c}{a} = 4$ $\Rightarrow$ Đáp số chính xác là C.
VD 6: (Thi thử chuyên Khoa học tự nhiên lần 1) Phương trình ${z^2} + i z + 1 = 0$ có bao nhiêu nghiệm trong tập số phức: A.2 B.1 C.0 D.Vô số
Lời giải: Ta phân biệt: Trên tập số thực phương trình bậc hai $a{x^2} + bx + c = 0$ sẽ có hai nghiệm phân biệt nếu $\Delta > 0$, có hai nghiệm kép nếu $\Delta = 0$, vô nghiệm nếu $\Delta < 0$. Vậy ta chỉ cần tính $\Delta$ là xong. Với phương trình ${z^2} + i z + 1 = 0$ thì $\Delta = {i^2} - 4 = - 5$ là một đại lượng phức.
VD7: (Thi thử chuyên Khoa học tự nhiên lần 2) Cho phương trình ${z^2} + 2{z^2} + 5 = 0$. Hãy tìm nghiệm phức của phương trình này?
Lời giải: Một cách đơn giản để giải phương trình này là sử dụng công thức nghiệm của phương trình bậc hai:
$x = \frac{{ - b \pm \sqrt {\Delta } }}{{2a}}$
Trong đó, $a = 1$, $b = 2$, $\Delta = {b^2} - 4ac = 4 - 4 \cdot 1 \cdot 5 = -16$
Vì $\Delta < 0$, nên phương trình không có nghiệm trong tập số phức.
Bài tập vận dụng
Bài 1. Cho phương trình $v$ có hai nghiệm phức ${z_1}$ và ${z_2}$. Giá trị của $|{z_1}| + |{z_2}|$ là: A. $2\sqrt {17}$ B. $2\sqrt {13}$ C. $2\sqrt {10}$ D. $2\sqrt {15}$
Bài 2. Gọi ${z_1},{z_2}$ là hai nghiệm của phương trình ${z^2} + 2{z^2} + 10 = 0$. Tính giá trị của biểu thức $A = |{z_1}|^2 + |{z_2}|^2$ A. $2\sqrt {10}$ B. 20 C. $5\sqrt {2}$ D. $10\sqrt {3}$
Bài 3. Kí hiệu ${z_1},{z_2},{z_3}$ là nghiệm của phương trình ${z^3} + 27 = 0$. Tính tổng $T = |{z_1}| + |{z_2}| + |{z_3}|$ A. T = 0 B. $T = 3\sqrt {3}$ C. T = 9 D. T = 3
Bài 4. Gọi ${z_1},{z_2},{z_3},{z_4}$ là bốn nghiệm phức của phương trình $2{z^4} - 3{z^2} - 2 = 0$. Tính tổng sau $T = |{z_1}| + |{z_2}| + |{z_3}| + |{z_4}|$ A. 5 B. $5\sqrt {2}$ C. $3\sqrt {2}$ D. $\sqrt {2}$
Bài 5. Xét phương trình ${z^3} = 1$ trên tập số phức. Tập nghiệm của phương trình là: A. $S = \left{ 1 \right}$ B. $S = \left{ {1;\frac{{ - 1 \pm \sqrt {3} }}{2}} \right}$ C. $S = \left{ {1; - \frac{1}{2} \pm \frac{{\sqrt {3} }}{2}i} \right}$ D. $S = \left{ { - \frac{1}{2} \pm \frac{{\sqrt {3} }}{2}i} \right}$
Bài 6. Biết z là nghiệm của phương trình $z + \frac{1}{z} = 1$. Tính giá trị biểu thức $P = {z^{2009}} + \frac{1}{{z^{2009}}}$ A. P = 1 B. P = 0 C. $P = - \frac{5}{2}$ D. $P = \frac{7}{4}$












