Giới thiệu
Bạn đã từng gặp khó khăn khi học lý thuyết phương trình mặt phẳng Oxyz lớp 12? Bài viết này sẽ cung cấp cho bạn những kiến thức căn bản về phương trình mặt phẳng và hướng dẫn giải các dạng bài tập một cách chi tiết.
Ôn tập lý thuyết phương trình mặt phẳng Oxyz lớp 12
Vectơ chỉ phương và vecto pháp tuyến của hai mặt phẳng
Để hiểu rõ hơn về vectơ pháp tuyến, chúng ta cần biết:
- Vectơ pháp tuyến của mặt phẳng (P) là một vectơ khác vectơ 0 có phương vuông góc với (P).
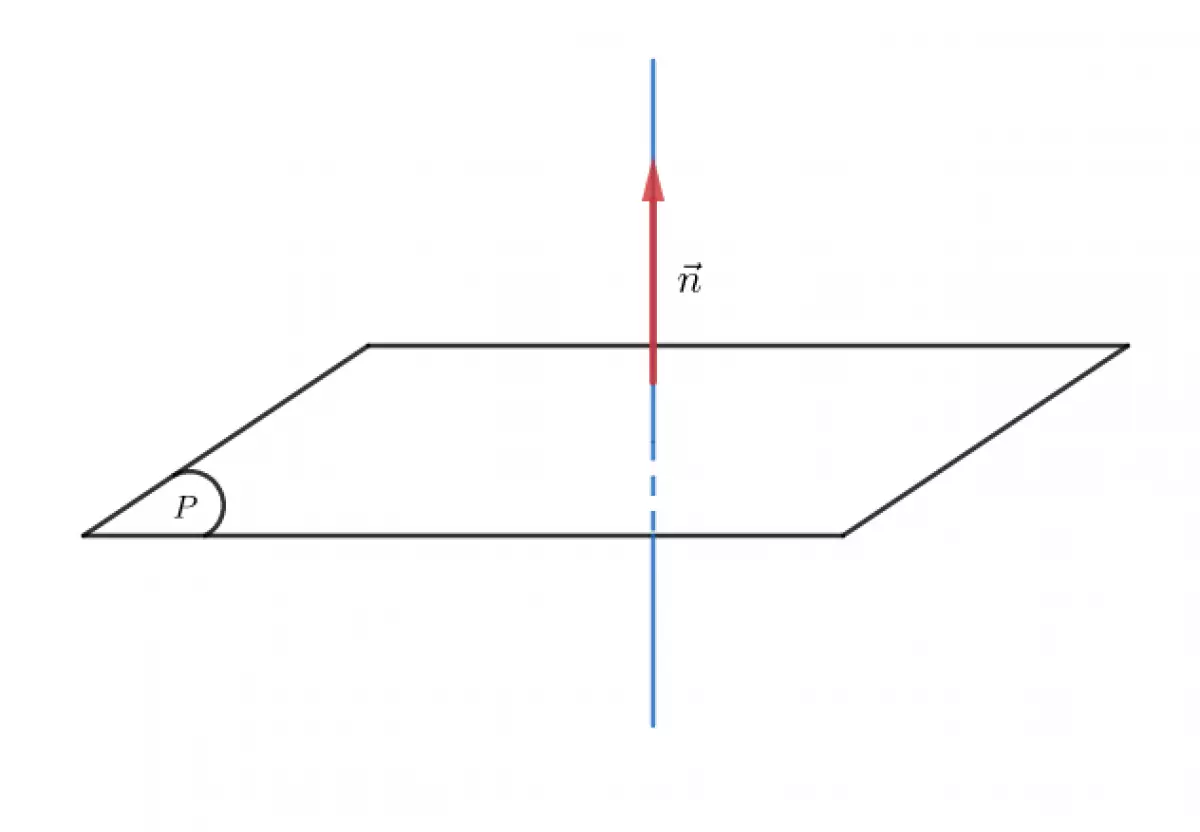
- Vectơ chỉ phương của mặt phẳng (P) là cặp vectơ không cùng phương mà giá trị của chúng nằm song song hoặc nằm trên mặt phẳng (P).
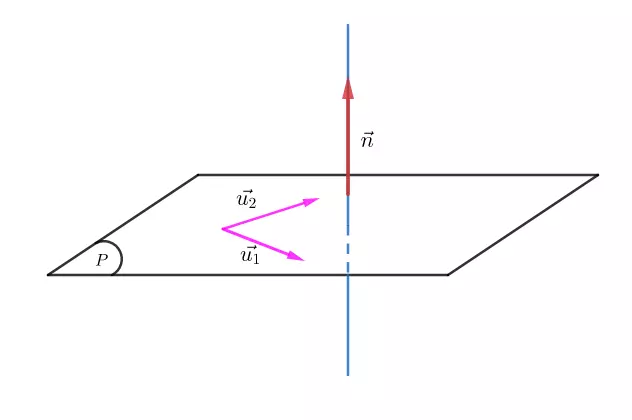
Phương trình mặt phẳng
- Phương trình mặt phẳng qua điểm M(x0, y0, z0) và có vectơ pháp tuyến n(A, B, C) được biểu diễn là: A(x - x0) + B(y - y0) + C(z - z0) = 0.
- Mặt phẳng trong không gian có phương trình tổng quát dạng: Ax + By + Cz = 0, trong đó A^2 + B^2 + C^2 > 0. Vectơ n(A, B, C) chính là vectơ pháp tuyến của mặt phẳng.
- Mặt phẳng đi qua 3 điểm M(a, 0, 0), N(0, b, 0), C(0, 0, c) với abc ≠ 0 có phương trình: (x/a) + (y/b) + (z/c) = 0. Phương trình này được gọi là phương trình mặt phẳng theo đoạn chắn.
Vị trí tương đối của hai mặt phẳng
Cho hai mặt phẳng (P1) và (P2), ta có phương trình như sau:
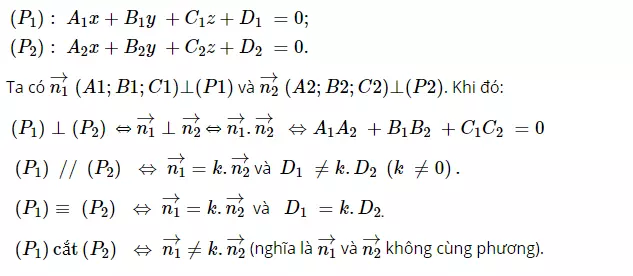
Góc giữa hai mặt phẳng
Cho hai mặt phẳng (P1) và (P2), ta có phương trình sau:
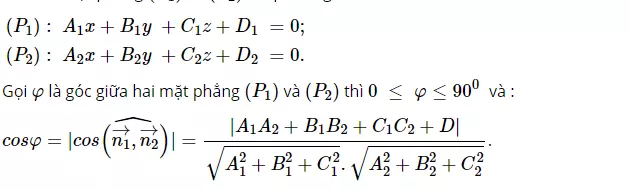
Khoảng cách từ 1 điểm đến mặt phẳng

Cách giải các dạng bài tập viết phương trình mặt phẳng trong không gian
Lập phương trình mặt phẳng oxyz đi qua 3 điểm
Phương trình tổng quát của mặt phẳng (P) trong không gian Oxyz có dạng: Ax + By + Cz + D = 0, với A^2 + B^2 + C^2 > 0. Để viết phương trình mặt phẳng, chúng ta cần có:
- Điểm M bất kỳ mà mặt phẳng đi qua.
- Vectơ pháp tuyến của mặt phẳng.
Viết phương trình mặt phẳng p song song và cách đều
Mặt phẳng (P) đi qua điểm M0(x0, y0, z0) đồng thời song song với mặt phẳng (Q). Phương trình của mặt phẳng (P) được biểu diễn là: A(x - x0) + B(y - y0) + C(z - z0) = 0. Lưu ý rằng hai mặt phẳng song song có cùng vectơ pháp tuyến.
Dạng bài tập viết phương trình mặt phẳng tiếp xúc mặt cầu
Trong dạng bài tập này, chúng ta cần làm như sau:
- Tính bán kính của mặt cầu S và tìm tọa độ tâm I.
- Nếu mặt cầu S tiếp xúc với mặt phẳng P tại M, thì mặt phẳng P sẽ đi qua điểm M và có vectơ pháp tuyến là MI.
- Trong trường hợp không có tiếp điểm được cho, chúng ta phải sử dụng các dữ liệu liên quan để tìm vectơ pháp tuyến của mặt phẳng. Sau đó, viết phương trình mặt phẳng dưới dạng Ax + By + Cz + D = 0.
Viết phương trình 2 mặt phẳng vuông góc
Để hai mặt phẳng vuông góc với nhau trong không gian Oxyz, ta cần thỏa mãn điều kiện: ${AA}'$ + ${BB}'$ + ${CC}'$ + ${DD}'$ = 0, với (P): Ax + By + Cz + D = 0 và (Q): ${A}'x$ + ${B}'y$ + ${C}'z$ + ${D}'$ = 0. Để chứng minh điều này, chúng ta có thể cách:
- Chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
- Chứng minh góc giữa hai mặt phẳng là 90 độ.
Viết phương trình mặt phẳng cắt 3 trục tọa độ
Trong dạng bài này, chúng ta có phương pháp cụ thể như sau:

Bài viết trên đã giúp bạn hiểu rõ về lý thuyết phương trình mặt phẳng Oxyz và cách giải các dạng bài tập thường gặp. Tuy nhiên, nếu bạn muốn đạt kết quả tốt hơn, hãy truy cập vào Vuihoc.vn để làm thêm nhiều dạng bài tập hình học không gian khác nhau. Chúc bạn thành công trong việc học toán và chuẩn bị cho kỳ thi THPT Quốc Gia sắp tới!












