Phân Tích Và Giải Phương Trình Bậc Nhất Bậc Hai Lớp 10
Phương trình quy về phương trình bậc nhất bậc hai là phương trình được viết theo dạng phương trình tổng quát có ẩn x. Để giải bài tập dạng này, chúng ta cần phân tích và giải phương trình theo ẩn.
Phương trình quy về bậc nhất
Phương trình bậc nhất có dạng tổng quát như sau:
y=ax+b (a≠0)
Khi a≠0: Phương trình có nghiệm duy nhất x=-b/a
Khi a=0, b≠0: Phương trình vô nghiệm.
Khi a=0, b=0: Phương trình có nghiệm đúng với mọi x∈R
Lưu ý: Phương trình ax+b=0 với a≠0 được gọi là phương trình bậc nhất một ẩn x.

Phương trình quy về bậc hai
Phương trình quy về bậc hai có dạng tổng quát như sau:
a^2+bx+c=0, (a≠0)
Δ=b^2-4ac gọi là biệt thức của phương trình.
-
Nếu Δ>0 thì phương trình có 2 nghiệm phân biệt: x1,2=(-b±√Δ)/(2a)
-
Nếu Δ=0 thì phương trình có nghiệm kép x=-b/(2a)
-
Nếu Δ<0 thì phương trình vô nghiệm

Định lý Vi-ét
Trong phương trình quy về phương trình bậc nhất bậc hai, định lý Vi-ét nói lên mối quan hệ giữa các hệ số và các nghiệm của một phương trình đa thức. Trong chương trình toán học, chúng ta sẽ rất dễ bắt gặp dạng bài về định lí Vi-ét này.
Phương trình ax^2+bx+c=0 (a≠0) có hai nghiệm x1, x2 thì: x1+x2=-b/a, x1x2=c/a
Ngược lại, nếu hai số u và v có tích uv=P và tổng u+v=S thì u và v là hai nghiệm của phương trình: x^2-Sx+P=0
Ví dụ 1: Hãy tìm tổng và tích của nghiệm phương trình x^2-8x+11=0
Giải: S=x1+x2=-(-8)/1=8
Ví dụ 2: Hãy tìm tổng và tích của nghiệm phương trình x^2+10x+25=0
Giải: S=x1+x2=-10
Phương trình chứa ẩn trong giá trị tuyệt đối
Để giải một phương trình chứa ẩn trong dấu giá trị tuyệt đối, chúng ta có phương pháp chính là đặt các điều kiện xác định để đưa phương trình có dấu giá trị tuyệt đối thành phương trình không có dấu giá trị tuyệt đối.
Ta có thể làm theo cách:
- Đặt ẩn phụ.
- Bình phương hai vế.
Với dạng phương trình |f(x)| = |g(x)| ta có phương pháp giải như sau:
Với dạng phương trình |f(x)| = g(x), ta có phương pháp chuyển đổi như sau:
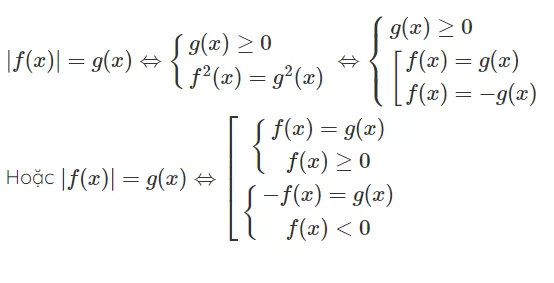
Phương trình chứa ẩn dưới dấu căn
Phương pháp chung để giải phương trình chứa ẩn dưới dấu căn là ta đặt điều kiện, sau đó lũy thừa một cách thích hợp hai vế của phương trình để làm mất dấu căn thức.
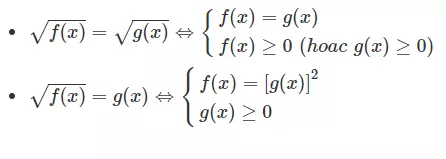
Ví dụ 1: Giải phương trình √(3x-5)=3
Giải: Đk: x≥5/3 √(3x-5)=0 x=14/3 (t/m)
Vậy phương trình có nghiệm x=14/3
Ví dụ 2: Giải phương trình √(2x+5)=2
Giải: Đk: x≥-5/2 √(2x+5)=4 x=-1/2
Vậy phương trình có nghiệm x=-1/2
Ví dụ 3: √(x^2+2x+4)=√(2-x)
Giải:

Một Số Bài Tập Phương Trình Quy Về Phương Trình Bậc Nhất Bậc Hai
Bài tập quy về phương trình bậc nhất bậc hai có rất nhiều dạng bài khác nhau, đòi hỏi học sinh cần nắm chắc kiến thức để áp dụng vào bài tập. Hãy cùng điểm qua những ví dụ dưới đây về bài tập quy về phương trình bậc nhất bậc hai nhé.
Bài tập 1: Giải phương trình sau và biện luận theo tham số m: m^2(x+1)-1=(2-m)x
Giải:

Bài tập 2: Cho phương trình: x^2-(2m+3)x+m^2-2m=0. Hãy tìm m để phương trình có 2 nghiệm phân biệt.
Giải: Để phương trình có 2 nghiệm phân biệt khi Δ > 0 Δ = (2m-3)^2-4(m^2-2m) = 4m+9 Δ > 0 ⇔ -4m+9 > 0 ⇔ m < 9/4
Vậy phương trình có hai nghiệm phân biệt khi m < 9/4.
Bài tập 3: Cho phương trình mx^2+(m^2-3)x+m=0. Tìm m để phương trình có nghiệm kép và tìm nghiệm kép đó.
Giải:

Bài tập 4: Hãy giải phương trình cho sau: |2x+1|=|x^2-3x-4|
Giải:

Bài tập 5: Tìm nghiệm của phương trình: 1+(2/(x-2))=(10/(x+3))-(50/((2-x)(x+3)))
Giải:

Đăng ký ngay khóa học DUO để được lên lộ trình ôn thi tốt nghiệp sớm nhất!

Hy vọng rằng qua các bài tập kèm lời giải trên sẽ giúp bạn hiểu và áp dụng kiến thức dễ dàng hơn đối với dạng bài phương trình quy về phương trình bậc nhất bậc hai. Truy cập ngay nền tảng học online Vuihoc.vn để ôn tập nhiều hơn về các dạng toán khác nhé! Chúc bạn ôn tập hiệu quả.












