Lý Thuyết Và Bài Tập Về Bất Phương Trình Bậc Nhất Hai Ẩn Lớp 10

Giới thiệu

Trong chương trình đại học THPT, bất phương trình bậc nhất hai ẩn là một phần kiến thức cực kỳ quan trọng mà học sinh cần nắm vững từ lớp 10. Trên thực tế, bất phương trình bậc nhất hai ẩn xuất hiện dưới một trong các dạng sau:

Trong các biểu thức trên: a, b, c là các số cho trước thỏa mãn điều kiện 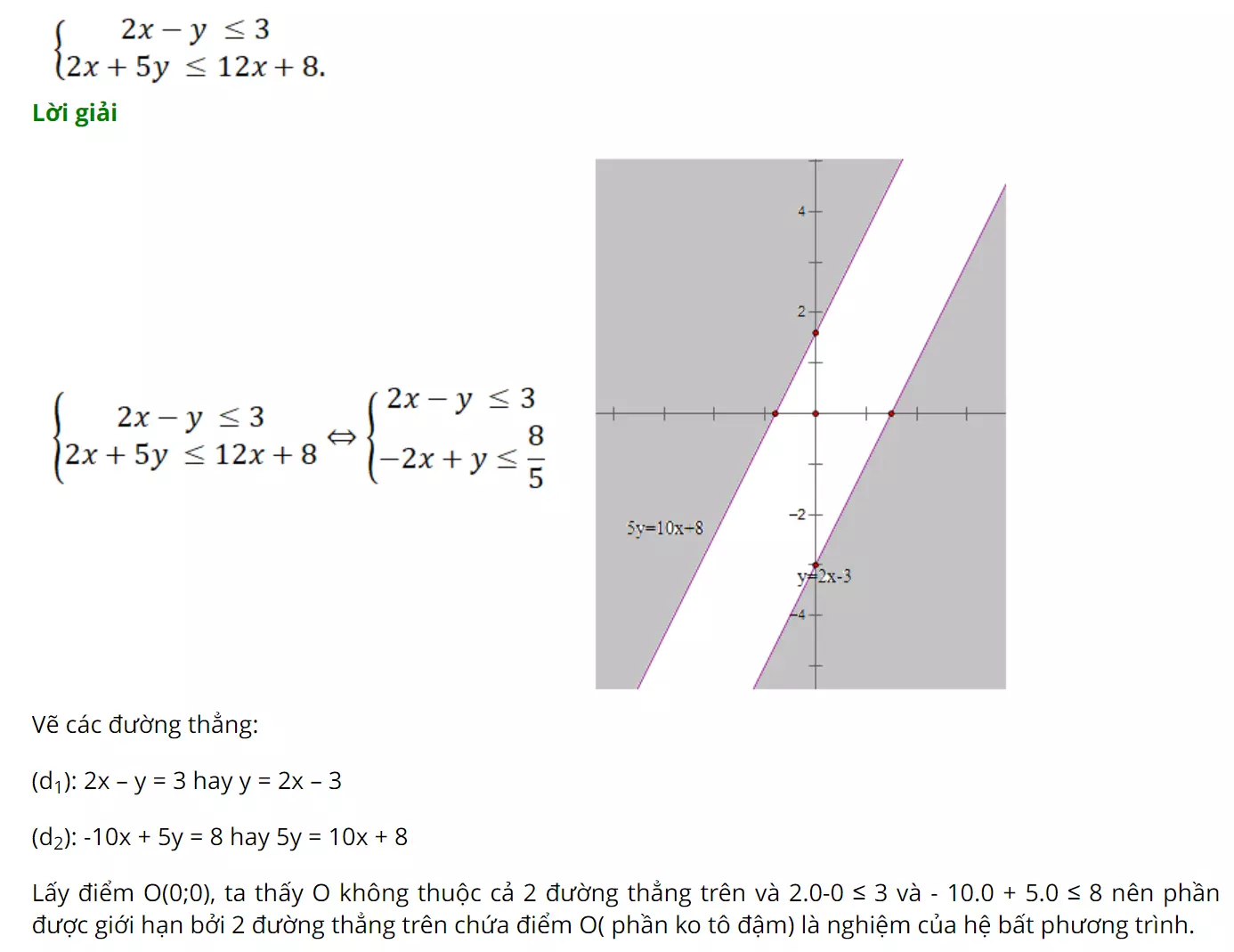, x và y là những ẩn số. Nghiệm của các bất phương trình bậc nhất hai ẩn được định nghĩa như sau:

Nếu có cặp số thỏa mãn 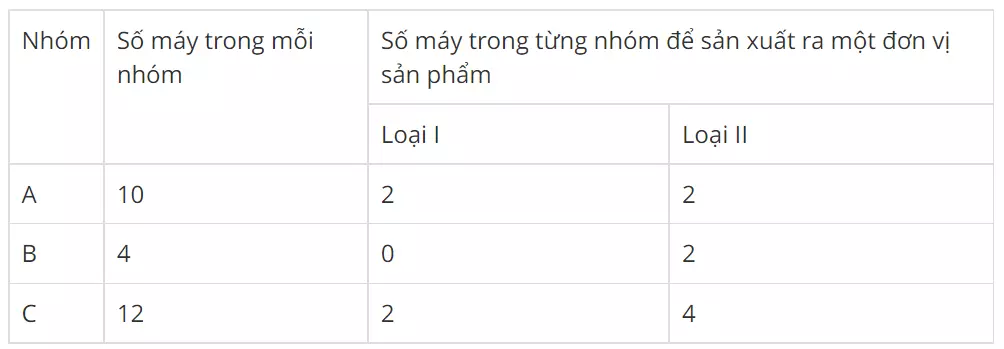, khi đó 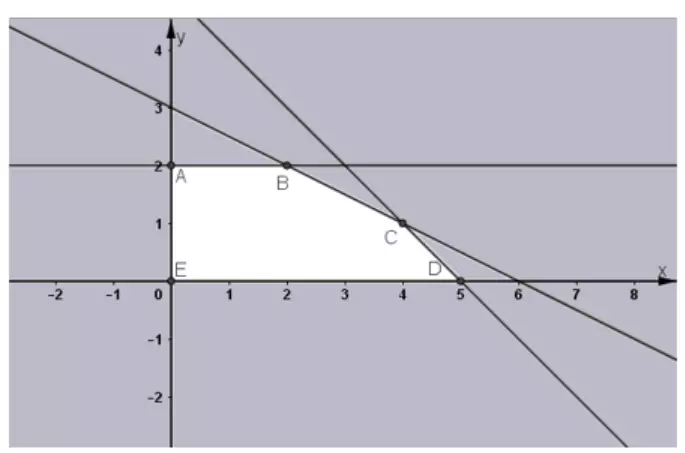được gọi là một nghiệm của bất phương trình . Tương tự, với các bất phương trình , và , cũng có các định nghĩa nghiệm tương tự.

Đăng ký ngay để được các thầy cô ôn tập và xây dựng lộ trình học tập THPT vững vàng

![]()

Miền nghiệm của bất phương trình 2 ẩn và cách biểu diễn

Định nghĩa

Miền nghiệm của một bất phương trình bậc nhất hai ẩn là tập hợp các điểm trong mặt phẳng tọa độ Oxy có tọa độ là nghiệm của bất phương trình đó.

Định lý

Cho đường thẳng (d): ax+by+c=0 chia mặt phẳng tọa độ Oxy thành 2 nửa mặt phẳng sao cho một trong 2 nửa mặt phẳng ấy gồm các điểm có tọa độ thỏa mãn ax+by+c>0, nửa còn lại gồm các điểm có tọa độ thỏa mãn ax+by+c<0. Từ đó, ta suy ra:

Nửa mặt phẳng (không kể bờ (d)) chứa M (x₀; y₀) là miền nghiệm của bất phương trình ax+by+c>0 (hay ax+by+c<0) nếu M (x₀; y₀) là nghiệm của bất phương trình đó.

Cách biểu diễn miền nghiệm

Để xác định miền nghiệm của bất phương trình bậc nhất hai ẩn, ta có thể sử dụng cách làm sau đây:

• Bước 1: Vẽ (d): ax+by+c=0
• Bước 2: Xác định 1 điểm M (x₀; y₀) sao cho M không nằm trên (d)

Trong bước 2 này, ta cần lưu ý 2 trường hợp:

• Trường hợp 1: Khi ax₀+by₀+c<0 thì lúc đó nửa mặt phẳng (không kể bờ (d)) chứa điểm M được gọi là miền nghiệm của bất phương trình ax+by+c<0.
• Trường hợp 2: Khi ax₀+by₀+c>0 thì lúc đó nửa mặt phẳng (không kể bờ (d)) chứa điểm M được gọi là miền nghiệm của bất phương trình ax+by+c>0.

Lưu ý:

• Khi biểu diễn miền nghiệm, đối với các bất phương trình có dạng ax+by+c₁ hoặc ax+by+c₂ thì khi đó miền nghiệm là nửa mặt phẳng kể cả bờ.
• Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

Cùng xem ví dụ dưới đây để hiểu rõ hơn về cách biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn:

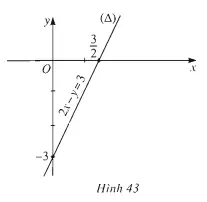
Ví dụ: Biểu diễn tập nghiệm của bất phương trình sau: 2x-y≤3

Giải:

Vẽ đường thẳng có 2x-y=3

Xét thấy c=3 > 0 nên miền nghiệm của bất phương trình 2x-y≤3 là nửa mặt phẳng bờ có chứa gốc tọa độ.

Hệ bất phương trình bậc nhất hai ẩn

Khi học về bất phương trình bậc nhất hai ẩn, không thể không đề cập đến hệ bất phương trình bậc nhất hai ẩn. Hệ bất phương trình bậc nhất hai ẩn bao gồm hai hoặc nhiều bất phương trình bậc nhất hai ẩn. Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ thỏa mãn mọi bất phương trình trong hệ thì tập hợp các điểm đó được gọi là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn. Ta cũng có thể hiểu miền nghiệm của hệ chính là giao các miền nghiệm của những bất phương trình thành phần trong hệ.

Để xác định được miền nghiệm của hệ bất phương trình bậc nhất hai ẩn, ta có thể sử dụng phương pháp biểu diễn hình học như sau:

• Bước 1: Xác định miền nghiệm của từng bất phương trình trong hệ và gạch bỏ miền còn lại
• Bước 2: Sau khi đã xác định các miền trong hệ, miền mà không bị gạch chính là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn đã cho.

Học sinh cùng VUIHOC xem ví dụ sau để hiểu cách giải một bài toán thực tế ứng dụng vào hệ bất phương trình bậc nhất hai ẩn:

Ví dụ (Toán 10 Đại số trang 97 SGK): Biểu diễn hình học miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau đây:

Hướng dẫn giải:

• Ta có:

Vẽ các đường thẳng:

(d1): 2x - y = 3 hay y = 2x - 3

(d2): -10x + 5y = 8 hay y = 2x +

Lấy điểm O (0; 0), ta thấy điểm O đều không thuộc 2 đoạn thẳng trên và khi thay 0 vào phương trình ta có 2.0 - 0 3 và 2.0 + 5.0 12.0 + 8 nên phần nằm trong được giới hạn của 2 đoạn thẳng trên (bao gồm cả điểm O) là nghiệm của hệ bất phương trình trên.

Một số bài tập về bất phương trình bậc nhất hai ẩn

Cách xác định miền nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Đối với các bài toán xác định miền nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn, ta cần làm theo các bước sau:

1. Xác định miền nghiệm của từng bất phương trình trong hệ và gạch bỏ miền còn lại
2. Sau khi đã xác định các miền trong hệ, miền mà không bị gạch chính là miền nghiệm của hệ bất phương trình bậc nhất hai ẩn

Cùng xem ví dụ sau để hiểu rõ hơn cách áp dụng giải một bài toán thực tế như thế nào:

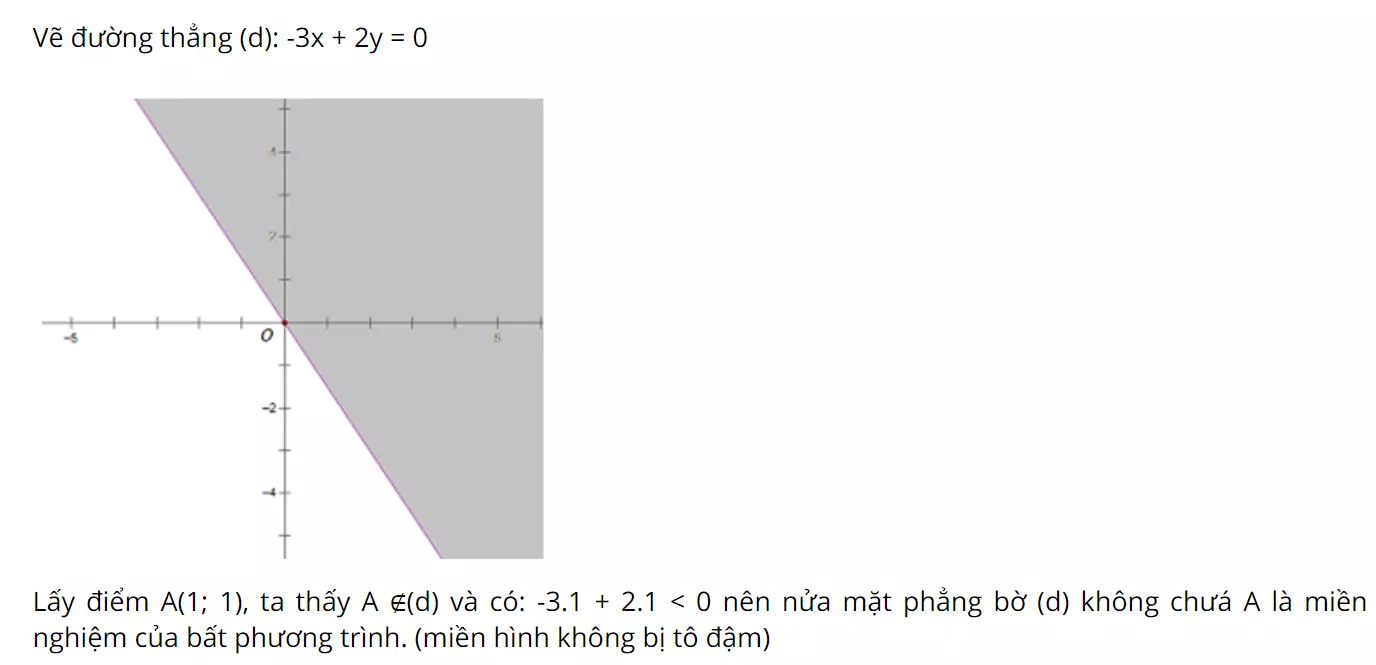
Ví dụ 1: Tìm tập nghiệm theo hình học của bất phương trình sau: -3x+2y > 0

Giải:

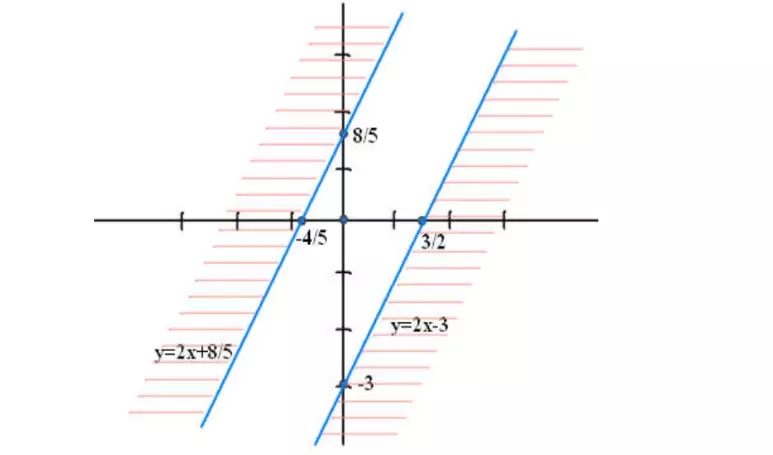
Ví dụ 2: Cho hệ bất phương trình sau, biểu diễn hình học tập nghiệm:

Vận dụng vào bài toán kinh tế

Bất phương trình và hệ bất phương trình bậc nhất hai ẩn cũng được ứng dụng rất nhiều vào các bài toán kinh tế. Dưới đây là một ví dụ mẫu để hiểu rõ hơn về cách giải các bài toán ứng dụng thú vị nhé!

Ví dụ 1: Hai loại sản phẩm I và II được sản xuất ra từ ba nhóm máy A, B, C. Khi sản xuất một đơn vị sản phẩm, mỗi loại phải dùng lần lượt các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được ghi trong bảng sau:

Một đơn vị sản phẩm I lãi 3 nghìn đồng.

Một đơn vị sản xuất II lãi 5 nghìn đồng.

Yêu cầu lập kế hoạch sản xuất sao cho tổng số tiền lãi đạt được cao nhất.

Giải:

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II sản xuất ra.

Như vậy tiền lãi có được là L = 3x + 5y (nghìn đồng).

Theo đề bài: Nhóm A cần 2x + 2y máy;

Nhóm B cần 0x + 2y máy;

Nhóm C cần 2x + 4y máy;

Vì số máy tối đa ở nhóm A là 10 máy, nhóm B là 4 máy, nhóm C là 12 máy nên x, y phải thỏa mãn hệ bất phương trình:

Khi đó bài toán mới hình thành: trong các nghiệm của hệ bất phương trình (1) thì nghiệm () nào cho L = 3x + 5y lớn nhất?

Miền nghiệm của hệ bất phương trình (1) là ngũ giác ABCDE tính cả miền trong.

Xét: L đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác ABCDE.

Tính giá trị của biểu thức L = 3x + 5y tại các đỉnh. Ta được:

Đỉnh A(0;2), L = 10

Đỉnh B(2; 2), L = 16

Đỉnh C(4; 1), L = 17

Đỉnh D(5; 0), L = 15

Đỉnh E(0; 0), L = 0

Do đó, L = 3x + 5y lớn nhất là 17 (nghìn đồng) khi: x = 4; y = 1

Kết luận: Để có tiền lãi cao nhất, nhà máy cần sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm loại II.

Trên đây là toàn bộ kiến thức về bất phương trình, hệ bất phương trình bậc nhất hai ẩn trong chương trình đại số THPT. Hy vọng rằng, bài viết đã cung cấp cho các em nguồn kiến thức hữu ích để vận dụng trong công cuộc ôn thi THPT quốc gia của mình. Để ôn tập lại các phần kiến thức Toán thi đại học khác, các em đừng quên truy cập vuihoc.vn và đăng ký khóa học để học thêm nhiều kiến thức bổ ích nhé!