Mặt phẳng tọa độ – Các dạng toán và phương pháp giải toán 7

Giới thiệu

Bạn đã từng nghe đến mặt phẳng tọa độ chưa? Đó là một khái niệm quan trọng trong toán học và có nhiều ứng dụng thú vị. Trên mặt phẳng tọa độ, chúng ta có thể biểu diễn các điểm bằng cách sử dụng các chỉ số số học. Trong bài viết này, chúng ta sẽ tìm hiểu về các dạng toán liên quan đến mặt phẳng tọa độ và phương pháp giải chúng.

Các dạng toán về mặt phẳng tọa độ

1. Mặt phẳng tọa độ

Mặt phẳng tọa độ Oxy là mặt phẳng được xác định bởi hai trục số vuông góc với nhau: trục hoành Ox và trục tung Oy. Điểm O là gốc tọa độ.

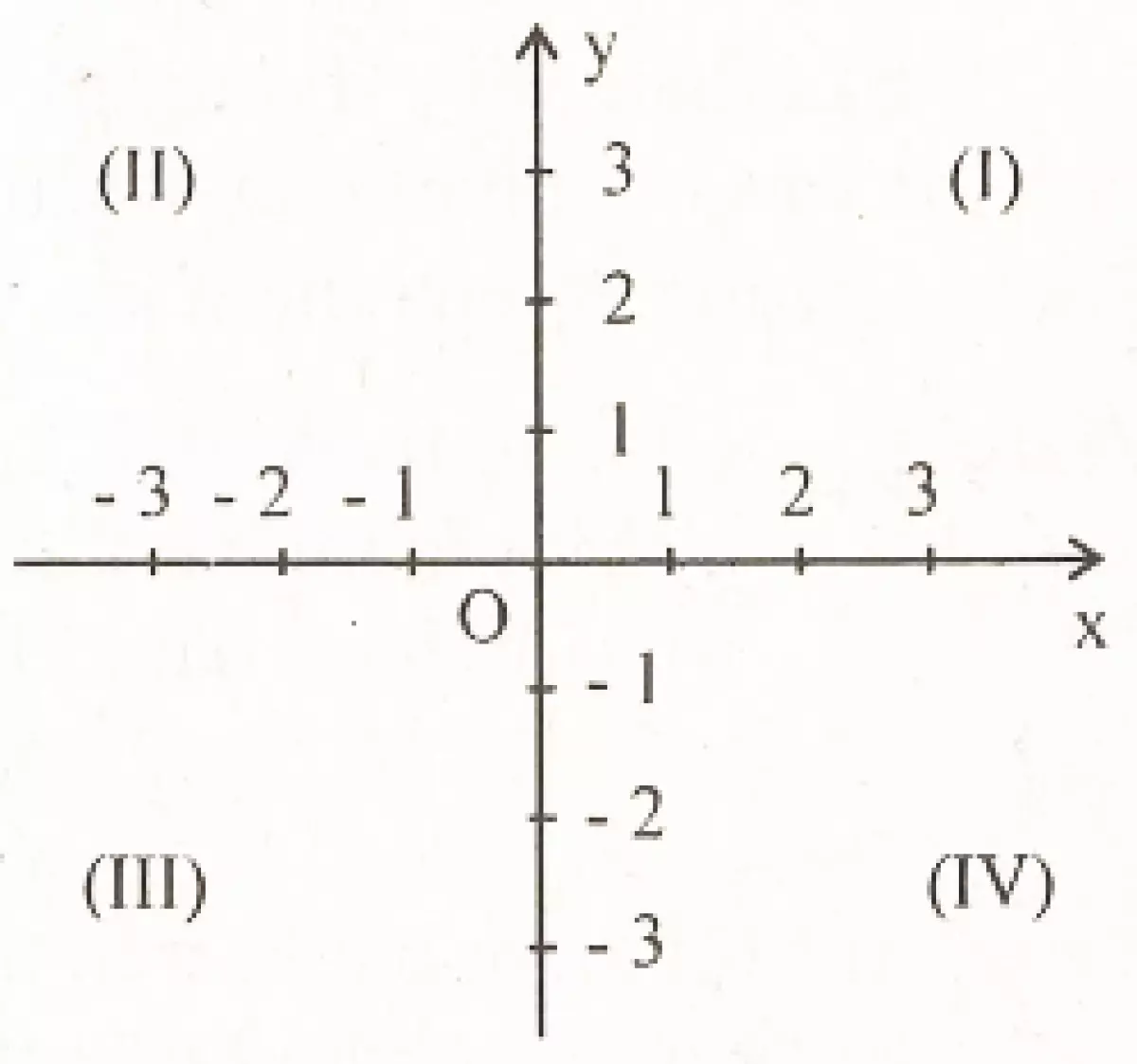
2. Tọa độ của một điểm

Trên mặt phẳng tọa độ, chúng ta biểu diễn các điểm bằng cách sử dụng tọa độ. Tọa độ của một điểm bao gồm hoành độ và tung độ.

Các dạng toán

Dạng 1. Viết tọa độ của các điểm cho trước trên mặt phẳng tọa độ

Phương pháp giải:

1. Từ điểm đã cho, vẽ đường thẳng song song với trục tung và cắt trục hoành tại một điểm biểu diễn hoành độ của điểm đó.
2. Từ điểm đã cho, vẽ đường thẳng song song với trục hoành và cắt trục tung tại một điểm biểu diễn tung độ của điểm đó.
3. Hoành độ và tung độ tìm được là tọa độ của điểm đã cho.

Ví dụ 1. (Bài 32 tr.67 SGK) a) Viết tọa độ các điểm M, N, P, Q trong hình 19 (SGK) b) Em có nhận xét gì về tọa độ của các điểm M và N, P và Q.

Giải. a) Trong hình 19 (SGK) ta xác định tọa độ của của điểm M, N, P, Q như sau: M(-3;2), N(2;-3), P(0;-2), Q(-2;0). b) Nhận xét: Trong mỗi cặp điểm M và N, P và Q ta nhận thấy hoành độ của điểm này bằng tung độ của điểm kia và ngược lại.

Ví dụ 2. (Bài 34 tr.68 SGK) a) Một điểm bất kỳ trên trục hoành có tung độ bằng bao nhiêu? b) Một điểm bất kỳ trên trục tung có hoành độ bằng bao nhiêu?

Trả lời. a) Một điểm bất kỳ trên trục hoành có tung độ bằng 0. b) Một điểm bất kỳ trên trục tung có hoành độ bằng 0.

Ví dụ 3. (Bài 35. tr.68 SGK) Tìm tọa độ các đỉnh của hình chữ nhật ABCD và của hình tam giác PQR trong hình 20 (SGK)

Trả lời. A(0,5;2), B(2;3), C(2;0), D(0;5;0), P(-3;3), Q(-1;1), R(-3;1).

Dạng 2. Biểu diễn các điểm có tọa độ cho trước trên mặt phẳng tọa độ

Phương pháp giải:

1. Từ điểm biểu diễn hoành độ của điểm cho trước, vẽ một đường thẳng song song với trục tung.
2. Từ điểm biểu diễn tung độ của điểm cho trước, vẽ một đường thẳng song song với trục hoành.
3. Giao điểm của hai đường thẳng vừa vẽ là điểm cần tìm.

Ví dụ 4. (Bài 33 tr.67 SGK)

Ví dụ 5. (Bài 346 tr.68 SGK) Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm: A(-4; -1); B(-2; -1); C(-2; -3); D(-4; -3). Tứ giác ABCD là hình gì?

Giải. Tứ giác ABCD là hình vuông.

Ví dụ 6. (Bài 37 tr.68 SGK) Hàm số y được cho trong bảng sau: a) Viết tất cả các cặp giá trị tương ứng (x;y) của hàm số trên. b) Vẽ một hệ trục tọa độ Oxy và xác định các điểm biểu diễn các cặp giá trị tương ứng của x và y ở câu a.

a) (0;0), (1;2), (2;4), (3;6), (4;8). b) Xem hình bên.

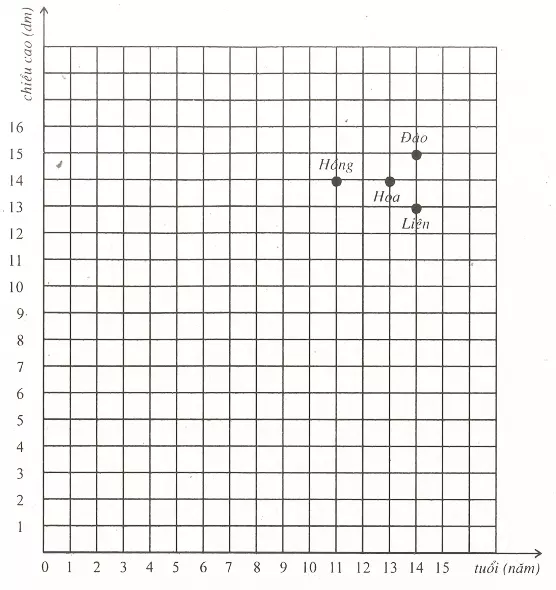
Dạng khác. Chiều cao và tuổi của bốn bạn Hồng, Hoa, Đào, Liên được biểu diễn trên mặt phẳng tọa độ (hình 21 SGK). Hãy cho biết a) Ai là người cao nhất và cao bao nhiêu? b) Ai là người ít tuổi nhất và bao nhiêu tuổi? c) Hồng và Liên ai cao hơn và ai nhiều tuổi hơn?

Trả lời. a) Đào là người cao nhất và cao 1,5m. b) Hồng 11 tuổi, là người ít tuổi nhất. c) Hồng cao hơn Liên nhưng Liên nhiều tuổi hơn Hồng.

Xem thêm Một số bài tập luyện tập về mặt phẳng tọa độ tại đây.

Xem thêm Đồ thị của hàm số y = ax (a ≠ 0) tại đây.

Bài viết này đã giới thiệu với bạn về mặt phẳng tọa độ và các dạng toán liên quan đến nó. Hi vọng những thông tin này sẽ giúp bạn hiểu rõ hơn về chủ đề này và có thể áp dụng vào thực tế. Cảm ơn bạn đã theo dõi!