Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu về một số kiến thức cơ bản liên quan đến số nguyên tố. Số nguyên tố là những số tự nhiên p (p > 1) chỉ có hai ước số là 1 và chính nó. Ví dụ về các số nguyên tố gồm: 2, 3, 5, 7, 11, 13, 17, 19, 23, ...
Chúng ta sẽ thực hiện một số thuật toán cơ bản bằng ngôn ngữ Java để giải quyết các bài toán sau:
- Kiểm tra xem một số tự nhiên n có phải là số nguyên tố hay không.
- Liệt kê các số nguyên tố trong đoạn [1, n].
Kiểm tra tính nguyên tố
Giải thuật thứ nhất
Ý tưởng của giải thuật này là kiểm tra xem có tồn tại một số nguyên k (2 ≤ k ≤ √n) là ước của n (n chia hết cho k) hay không. Nếu có, thì n không phải là số nguyên tố; ngược lại, n là số nguyên tố.
Chúng ta sẽ tạo một Java Project trong Eclipse IDE và đặt tên là JavaAlgorithmBasicProject. Tiếp theo, tạo package main và class Main.java với phương thức main() mặc định.
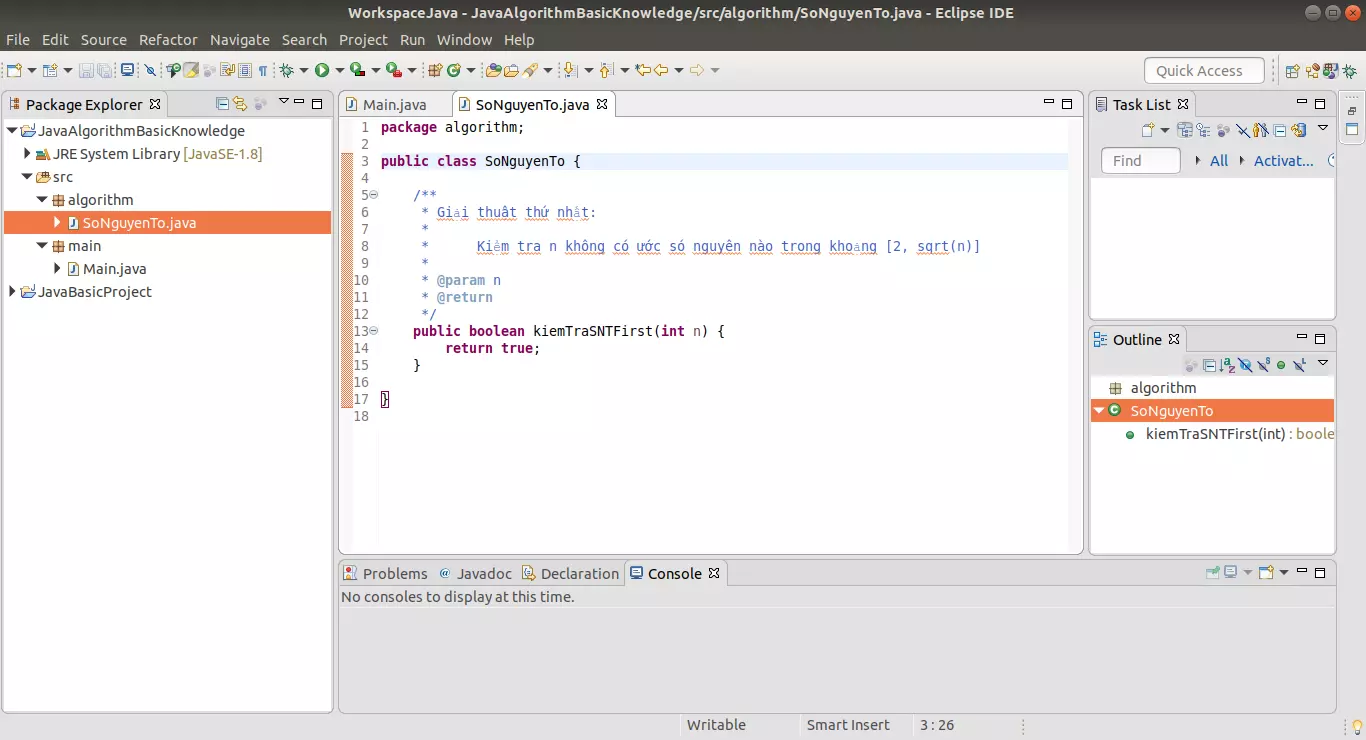
Tiếp theo, chúng ta tạo package algorithm và class SoNguyenTo.java. Trong class này, chúng ta sẽ tạo phương thức kiemTraSNTFirst() với các tham số và kiểu dữ liệu như sau:
- Tham số: một số tự nhiên n.
- Kiểu dữ liệu trả về: boolean (true nếu n là số nguyên tố, false nếu không phải).

Sau đó, chúng ta thực hiện giải thuật bằng ngôn ngữ Java như sau:
- Sử dụng phương thức Math.sqrt() để tính căn bậc hai của một số tự nhiên n.
- Sử dụng phương thức Math.round() để lấy phần nguyên của một số thập phân.
- Thư viện Math định nghĩa các phương thức dùng để tính toán các biểu thức toán học cơ bản. Các phương thức này có thể được gọi trực tiếp bằng cú pháp Math.phương_thức().
Tiếp theo, chúng ta thực hiện thử nghiệm phương thức kiemTraSNTFirst() trong class Main.java.
Cuối cùng, chúng ta thực thi toàn bộ project để kiểm tra kết quả thử nghiệm.
Giải thuật thứ hai
Ý tưởng của giải thuật này là kiểm tra các số k có tính chất giống với một trong hai tính chất cơ bản của số nguyên tố sau:
- Trừ số 2 và các số nguyên tố, các số khác đều là số lẻ.
- Trừ số 2, 3, các số nguyên tố có dạng 6k ± 1 (vì số có dạng 6k ± 2 thì chia hết cho 2, số có dạng 6k ± 3 thì chia hết cho 3).
Chúng ta thực hiện giải thuật bằng ngôn ngữ Java như sau:
Tiếp theo, chúng ta thực hiện thử nghiệm phương thức kiemTraSNTSecond() trong class Main.java.
Cuối cùng, chúng ta thực thi toàn bộ project để kiểm tra kết quả thử nghiệm.
Liệt kê các số nguyên tố trong đoạn [1, N]
Giải thuật thứ nhất
Ý tưởng của giải thuật này là chúng ta sẽ lần lượt xem xét các số m trong đoạn [1, n], rồi kiểm tra tính nguyên tố của m.
Chúng ta thực hiện giải thuật bằng ngôn ngữ Java như sau:
Java cung cấp cho chúng ta một số kiểu dữ liệu lưu trữ tập hợp các phần tử, trong đó List được sử dụng để lưu trữ không giới hạn các phần tử có thể trùng nhau. Để xác định kiểu dữ liệu cho toàn bộ các phần tử trong danh sách, chúng ta sử dụng cặp dấu <>.
Tiếp theo, chúng ta thực hiện thử nghiệm phương thức lietKeSNTFirst() trong class Main.java.
Cuối cùng, chúng ta thực thi toàn bộ project để kiểm tra kết quả thử nghiệm.
Giải thuật thứ hai
Ý tưởng của giải thuật này là chúng ta áp dụng sàng Eratosthenes để tìm các số nguyên tố nhỏ hơn hoặc bằng một số tự nhiên n. Cụ thể, chúng ta thực hiện các bước sau:
- Tạo một danh sách các số tự nhiên liên tiếp từ 2 đến n.
- Giả sử tất cả các số trong danh sách đều là số nguyên tố, trong đó số 2 là số nguyên tố đầu tiên.
- Đánh dấu các bội số của số nguyên tố p (2p, 3p, 4p, ...) không phải là số nguyên tố.
- Tìm các số còn lại trong danh sách mà chưa bị đánh dấu và lớn hơn p. Nếu không còn số nào, dừng tìm kiếm. Ngược lại, gán cho p giá trị của số nguyên tố tiếp theo và quay lại bước 3.
Khi giải thuật kết thúc, tất cả các số chưa bị đánh dấu trong danh sách là các số nguyên tố cần tìm.
Chúng ta thực hiện giải thuật bằng ngôn ngữ Java như sau:
Tiếp theo, chúng ta thực hiện thử nghiệm phương thức lietKeSNTSecond() trong class Main.java.
Cuối cùng, chúng ta thực thi toàn bộ project để kiểm tra kết quả thử nghiệm.
Tổng kết
Trong bài viết này, chúng ta đã cùng nhau tìm hiểu về một số giải thuật cơ bản xung quanh số nguyên tố và thực hiện chúng bằng ngôn ngữ Java. Hy vọng rằng những kiến thức và kỹ thuật đã được trình bày sẽ hữu ích cho các bài viết tiếp theo.












