Nhị thức Newton: Công thức sáng tạo và ứng dụng

Nhị thức Newton: Công thức quan trọng trong toán học

Nhị thức Newton là một định lý toán học quan trọng về việc khai triển hàm mũ của tổng. Nhìn chung, nhị thức Newton được ứng dụng rộng rãi trong nhiều bài toán chứng minh dãy số, các phép tính tổ hợp chỉnh hợp và các phép tính tổ hợp quan trọng khác.

Trong bài viết này, chúng ta sẽ tìm hiểu tổng quan về công thức, cách khai triển, công thức của tam giác Pascal (hệ quả) và ứng dụng vào một số dạng bài tập đặc trưng.

Hình ảnh minh họa

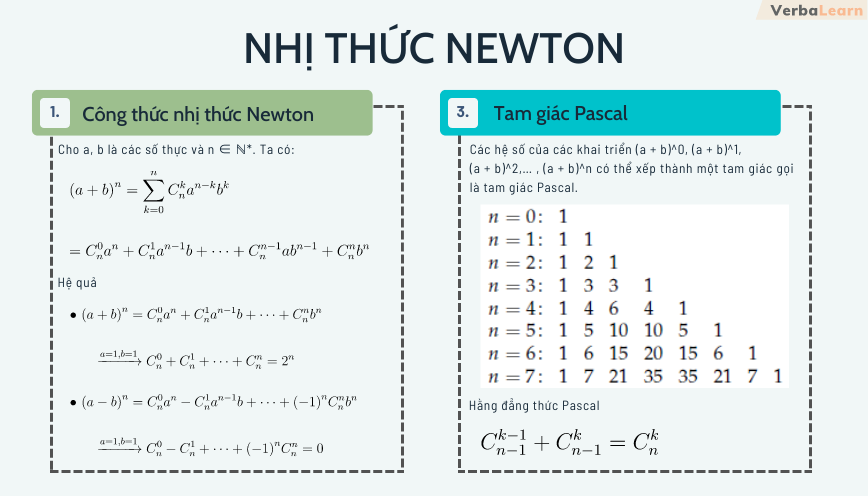
Công thức nhị thức Newton

Cho a, b là các số thực và n ∈ ℕ*. Ta có công thức nhị thức Newton như sau:

Ví dụ về khai triển nhị thức Newton

Ví dụ 1. Khai triển các nhị thức sau:

a) (x + 1)⁴

b) (x + 2y)⁵

c) ...

Hướng dẫn giải

a) Để khai triển nhị thức (x + 1)⁴ ta sử dụng công thức nhị thức Newton:

            (a + b)ⁿ = C(n, 0)·aⁿ·b⁰ + C(n, 1)·aⁿ⁻¹·b¹ + C(n, 2)·aⁿ⁻²·b² + ... + C(n, n)·a⁰·bⁿ

Với a = x, b = 1 và n = 4, ta có:

            (x + 1)⁴ = C(4, 0)·x⁴·1⁰ + C(4, 1)·x³·1¹ + C(4, 2)·x²·1² + C(4, 3)·x¹·1³ + C(4, 4)·x⁰·1⁴              (x + 1)⁴ = C(4, 0)·x⁴ + C(4, 1)·x³·1 + C(4, 2)·x²·1² + C(4, 3)·x¹·1³ + C(4, 4)·1⁴              (x + 1)⁴ = x⁴ + 4x³ + 6x² + 4x + 1

Vậy, khai triển của nhị thức (x + 1)⁴ là x⁴ + 4x³ + 6x² + 4x + 1.

b) Để khai triển nhị thức (x + 2y)⁵, ta sử dụng công thức nhị thức Newton như trên và thay a = x, b = 2y, n = 5:

            (x + 2y)⁵ = C(5, 0)·x⁵·(2y)⁰ + C(5, 1)·x⁴·(2y)¹ + C(5, 2)·x³·(2y)² + C(5, 3)·x²·(2y)³ + C(5, 4)·x¹·(2y)⁴ + C(5, 5)·x⁰·(2y)⁵              (x + 2y)⁵ = x⁵ + 10x⁴y + 40x³y² + 80x²y³ + 80xy⁴ + 32y⁵

Vậy, khai triển của nhị thức (x + 2y)⁵ là x⁵ + 10x⁴y + 40x³y² + 80x²y³ + 80xy⁴ + 32y⁵.

Tiếp tục phần còn lại của bài viết