Xin chào các bạn! Trong bài viết trước, chúng ta đã tìm hiểu về thuật toán Quy hoạch động thông qua những ví dụ đơn giản và dễ hiểu. Hôm nay, mình sẽ giới thiệu một bài toán phức tạp hơn, đó là Bài toán cái túi (Knapsack Problem).
Đây là một bài toán nhỏ để các bạn có thể áp dụng những kiến thức đã học vào những bài toán khó hơn. Hãy cùng tìm hiểu và làm quen với bài toán này nhé.
Mô tả bài toán
- Bài toán cái túi (Knapsack Problem) là một bài toán trong đó chúng ta có một cái túi có dung lượng giới hạn. Mục tiêu của chúng ta là chọn những đồ vật để chất vào túi sao cho tổng trọng lượng của chúng không vượt quá dung lượng của túi và tổng giá trị của chúng là lớn nhất.
Cụ thể, chúng ta có n đồ vật, đồ vật thứ i có trọng lượng W_i và giá trị C_i với i = 1, 2, ..., n. Nhiệm vụ của chúng ta là tìm cách chọn các đồ vật này để chất vào túi có dung lượng là b sao cho tổng trọng lượng của các đồ vật không vượt quá b và tổng giá trị của chúng là lớn nhất.
Đi tìm lời giải bằng thuật toán Quy hoạch động
Cùng đi tìm lời giải bài toán này bằng thuật toán Quy hoạch động nhé!
Có hai bước chính để giải bài toán này:
-
Phân rã: Chia bài toán ban đầu thành những bài toán con nhỏ hơn mà chúng ta có thể giải trực tiếp. Điều này giúp chúng ta giải quyết bài toán ban đầu một cách hiệu quả hơn.
-
Tổng hợp: Tổng hợp lời giải của các bài toán con kích thước nhỏ hơn để tạo thành lời giải cho bài toán lớn hơn.
Giải thuật
Dưới đây là giải thuật để giải bài toán cái túi:
Procedure Bag_best { For L= 0 to b do MaxV[0,L] = 0 ; For i= 0 to n do MaxV[i,0] = 0 ; For i = 1 to n do For L = 1 to b do { MaxV[i,L] = MaxV[i-1,L]; If [(L >= w[i]) && (MaxV[i-1,L-w[i]]+c[i] > MaxV[i-1, L])] MaxV[i, L] = MaxV[i-1,L-w[i]]+c[i] ; } return MaxV(n, b) ; }Một ví dụ cụ thể
Giả sử chúng ta có 6 đồ vật (n = 6), và túi có trọng lượng b = 19. Các đồ vật có trọng lượng và giá trị như sau:
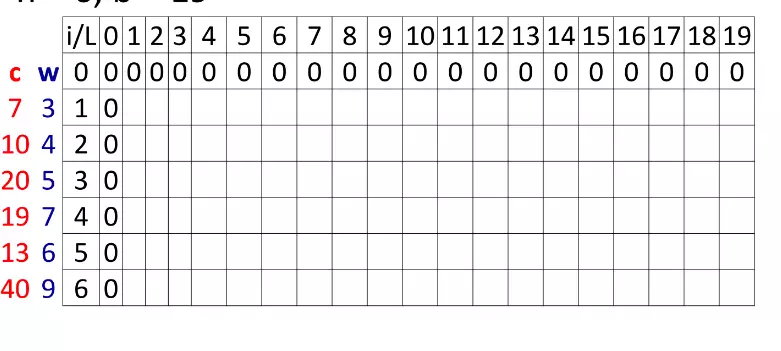
-
Khởi tạo: MaxV[0,L] = 0 , MaxV[i,0] = 0
-
Áp dụng giải thuật:

- Lặp đến hết, ta được kết quả:

Kết quả:
- Những vật được mang đi: {2, 3, 6}
- Tổng trọng lượng vật: 18
- Tổng giá trị: 70
Kết luận
Qua bài viết này, chúng ta đã tìm hiểu về thuật toán Quy hoạch động và áp dụng nó vào bài toán cái túi. Để giải quyết bài toán này, chúng ta cần áp dụng công thức Quy hoạch động theo ba bước: Phân rã, Giải các bài toán con và ghi nhận lời giải, và Tổng hợp lời giải.
Hy vọng rằng bài viết này đã giúp các bạn hiểu rõ hơn về thuật toán Quy hoạch động và cách áp dụng nó vào bài toán cái túi. Nếu có bất kỳ câu hỏi hoặc ý kiến gì, đừng ngần ngại để lại cho mình dưới phần bình luận nhé!













