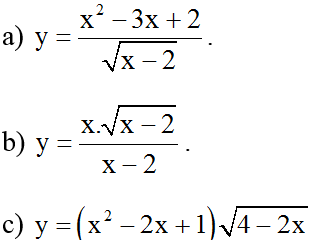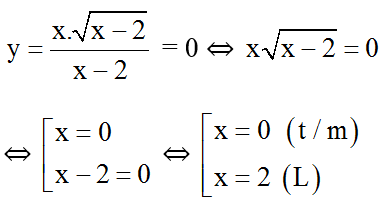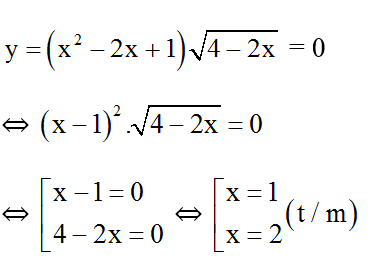Giới thiệu về phương pháp tìm tập giá trị của hàm số và cách giải các ví dụ minh họa.
Phương pháp giải
Cho một hàm số y = f(x). Tại mỗi giá trị x = xo, ta có duy nhất giá trị yo = f(xo) được gọi là giá trị của hàm số tại điểm xo. Để tìm giá trị của hàm số y = f(x) tại điểm xo, ta cần kiểm tra xem xo có nằm trong tập xác định của hàm số hay không.
Ví dụ minh họa
Ví dụ 1: Tìm giá trị của hàm số y = f(x) = 2x - 3
- Tập xác định: R (tất cả các số thực)
- f(0) = 2.0 - 3 = -3
- f(3/2) = 2.3/2 - 3 = 0
- f(-2) = 2.(-2) - 3 = -7
- f(3) = 2.3 - 3 = 3
- f(x+2) = 2.(x+2) - 3 = 2x + 4 - 3 = 2x + 1
Ví dụ 2: Tìm các giá trị của x sao cho y = 0 với:
- Với điều kiện x > 2:
- x^2 - 3x + 2 = 0
- (x - 1)(x - 2) = 0
- x = 1 hoặc x = 2 (không thỏa mãn điều kiện)
- Với điều kiện x ≠ 2:
- Với x = 0, y = 0
- Với điều kiện x ≤ 2:
- Với x = 1 hoặc x = 2, y = 0
Ví dụ 3: Tìm giá trị lớn nhất của các hàm số sau:
a) y = 5 - 4x - x^2 b) y = 3 - |x+1| c) y = 2x + 3 với |x| ≤ 2
- a) y = 5 - 4x - x^2 = 9 - (4 + 4x + x^2) = 9 - (x + 2)^2
- Vì (x + 2)^2 ≥ 0 nên 9 - (x + 2)^2 ≤ 9
- Hay y = 5 - 4x - x^2 ≤ 9
- Dấu " = " xảy ra khi (x + 2)^2 = 0 ⇒ x = -2
- Vậy hàm số đạt giá trị nhỏ nhất bằng 9 tại x = -2.
- b) Ta có: |x+1| ≥ 0 với mọi x
- ⇒ 3 - |x+1| ≤ 3 với mọi x
- Dấu " = " xảy ra khi x + 1 = 0 ⇒ x = -1
- Vậy hàm số y = 3 - |x+1| đạt giá trị lớn nhất bằng 3 khi x = -1.
- c) Ta có: |x| ≤ 2
- ⇒ -2 ≤ x ≤ 2
- ⇒ -4 ≤ 2x ≤ 4
- ⇒ -1 ≤ 2x + 3 ≤ 7
- Vậy giá trị lớn nhất của hàm số y = 2x + 3 với x thỏa mãn |x| ≤ 2 là 7 khi x = 2.
Bài tập trắc nghiệm tự luyện
Bài 1: Cho hàm số y = -x^2 + 2x + 3. Giá trị của hàm số tại x = √3 - 1 là: A. 5 B. 4√3 - 3 C. 4√3 + 3 D. 4√3 - 2
Bài 2: Giá trị hàm số tại x = 5 là: A. 1/2 B. Không tồn tại C. 1/4 D. -1/4.
Bài 3: Hàm số y = x - 1/x bằng không tại x bằng: A. x = ±2 B. x = 0 C. x = ±1 D. x = 2.
Bài 4: Giá trị nhỏ nhất của hàm số y = x^2 + 2x - 2 bằng: A. -2 B. -3 C. 0 D. 2.
Bài 5: Giá trị lớn nhất của hàm số bằng: A. 3 B. 4 C. 5 D. 6
Bài 6: Cho hàm số y = f(x) = Tính f(-3); f(-2); f(-1); f(0); f(3); f(5).
- Điều kiện x > 1 hoặc x < 1
- Ta có: y = f(x) =
- f(-3) = [Ảnh của hàm số tại x = -3]
- f(-2) = [Ảnh của hàm số tại x = -2]
Bài 7: Cho các hàm số: a) y = x - 1/x b) y = x^2 + 2x - 1 c) y = x^2 - 2√(x^2 - 1) Tìm các giá trị của x để giá trị của các hàm số trên bằng 0.
Bài 8: Tìm giá trị nhỏ nhất của các hàm số: a) y = x^2 + 2x + 4 b) y = 1/3 c) y = 1/3
Bài 9: Tìm giá trị lớn nhất của các hàm số: a) y = -x^2 + 2x + 4 b) y = 1 c) y = √5
Bài 10: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
- Điều kiện: 1 - 4x - x^2 ≥ 0
- Ta có: [Ảnh của hàm số tại x = -2√5 - 2]
- Dấu "=" khi 1 - 4x - x^2 = 0
- ⇒ 5 - (4 + 4x + x^2) = 0
- ⇒ 5 - (x + 2)^2 = 0
- ⇒ (x + 2)^2 = 5
- ⇒ x = -2±√5
- Vậy hàm số đạt giá trị nhỏ nhất bằng 0 tại x = -2±√5.
- Lại có: [Ảnh của hàm số tại x = -2]
- Vậy hàm số đạt giá trị lớn nhất bằng √5 tại x = -2.
Đây là một số ví dụ cơ bản về phương pháp tìm tập giá trị của hàm số. Còn nhiều dạng bài toán khác mà bạn có thể tìm hiểu thêm. Hy vọng các ví dụ trên sẽ giúp bạn hiểu rõ hơn về phương pháp này. Chúc bạn thành công!