Phương trình bậc hai là một khái niệm quen thuộc trong toán học. Nó giúp chúng ta tìm ra giá trị của biến số trong một phương trình hai bậc. Với phương trình bậc hai, việc giải nhanh và chính xác rất quan trọng. Đó là lý do tại sao bảng tính trực tuyến của HocTapHay.Com là một công cụ hữu ích để giải phương trình bậc 2 một cách đơn giản và chính xác.
Độ Thị
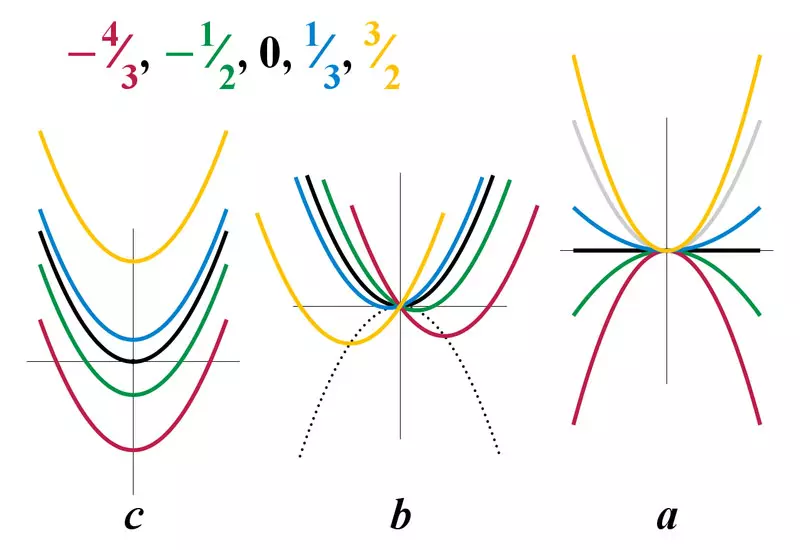(x_{1, 2} = frac{-b ± sqrt{b^2 - 4ac}}{2.a})
Trong toán học, đặc biệt là đại số sơ cấp, phương trình bậc hai có dạng: (ax^2 + bx + c = 0). Đây là một phương trình đa thức, trong đó x là biến số chưa biết, a, b và c là các hệ số đã biết. Phương trình bậc hai có một ẩn nên được gọi là "đơn biến". Phương trình này chỉ chứa các lũy thừa của x và bậc cao nhất của nó là hai.
Có nhiều phương pháp phổ biến để giải phương trình bậc hai, bao gồm phân tích thành nhân tử, phương pháp phần bù bình phương, sử dụng công thức nghiệm và đồ thị. Các phương pháp này đã được biết đến từ hàng nghìn năm trước Công Nguyên.
Giải Phương Trình Bậc Hai
Một phương trình bậc hai có thể có hai nghiệm, được gọi là các nghiệm. Hai nghiệm này có thể phân biệt hoặc không, và có thể là số thực hoặc không.
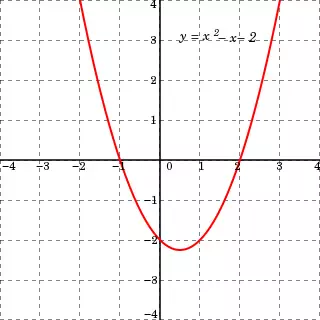Hình 1. Đồ thị của hàm số bậc hai (y = ax^2 + bx + c) với mỗi hệ số biến đổi trong khi các hệ số khác giữ nguyên tại giá trị a = 1, b = 0, c = 0. Ví dụ, đồ thị bên phải là của hàm số (y = ax^2) (b = c = 0 không đổi) ứng với các giá trị a thay đổi là (-frac{4}{3}, -frac{1}{2}, 0, frac{1}{3},) và (frac{3}{2}) (màu sắc tương ứng); tương tự đồ thị ở giữa là của hàm số (y = x^2 + bx) và đồ thị bên trái là của hàm số (y = x^2 + c).
Phương trình bậc hai có thể giải bằng phân tích thành nhân tử bằng cách kiểm tra. Đây là phương pháp đầu tiên mà hầu hết các học sinh được tiếp cận. Nếu phương trình có dạng (x^2 + bx + c = 0), ta có thể cố gắng phân tích vế trái thành ((x + q)(x + s)), trong đó q và s có tổng bằng -b và tích bằng c. Đây cũng được gọi là "quy tắc Việt". Phương pháp này chỉ áp dụng được cho những phương trình có nghiệm hữu tỉ.
Một phương pháp khác là phương pháp phần bù bình phương. Trên đồ thị, chúng ta tìm các điểm giao với trục hoành để tìm nghiệm của phương trình.
Công Thức Nghiệm
Công thức nghiệm là một công thức tổng quát để giải phương trình bậc hai. Nó được áp dụng bằng phương pháp phần bù bình phương. Công thức này cho ta giá trị của x trong phương trình (ax^2 + bx + c = 0) như sau: (x = frac{-b ± sqrt{b^2 - 4ac}}{2a}).
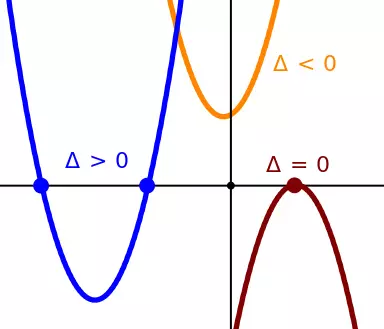Hình 2. Đồ thị hàm số bậc hai (y = x^2 - x - 2). Các hoành độ giao điểm của đồ thị với trục hoành x = -1 và x = 2 là nghiệm của phương trình bậc hai (x^2 - x - 2 = 0).
Có nhiều cách để rút ra công thức nghiệm, và công thức này có thể được tìm thấy trong tài liệu. Nhưng công thức được giới thiệu ở đây là công thức phổ biến và dễ hiểu. Nó cho ta nghiệm của phương trình bậc hai một cách chính xác.
Biệt Thức
Trong công thức nghiệm của phương trình bậc hai, biểu thức dưới dấu căn được gọi là biệt thức và thường được ký hiệu Δ. Biệt thức này quyết định số lượng và bản chất của nghiệm của phương trình.
Khi Δ > 0, phương trình bậc hai có hai nghiệm phân biệt. Khi Δ = 0, phương trình có một nghiệm kép. Khi Δ < 0, phương trình không có nghiệm thực.
Vậy biệt thức Δ quyết định số lượng và tính chất của nghiệm của phương trình.
Diễn Giải Bằng Hình Học
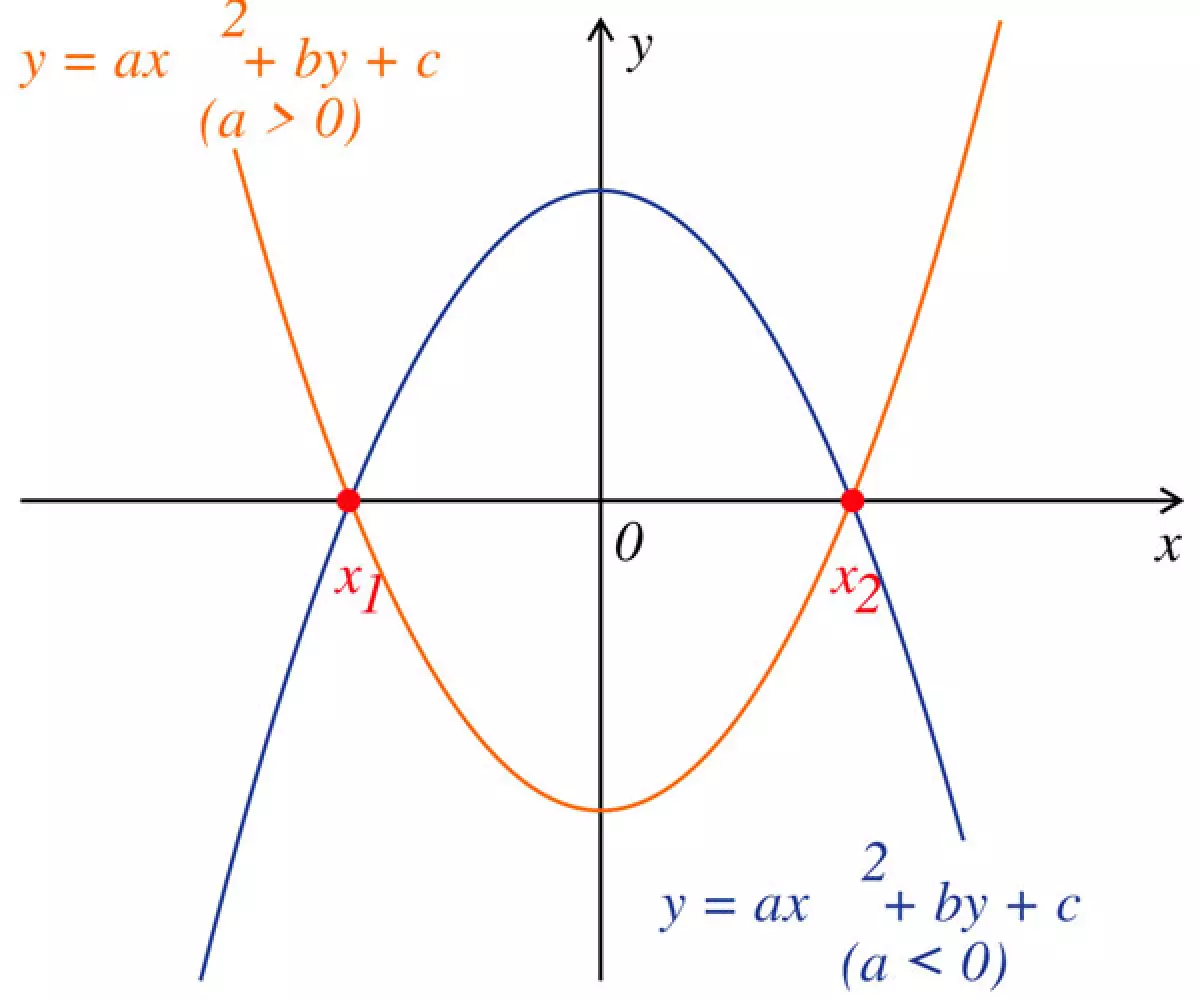
Hàm số (f(x) = ax^2 + bx + c) là hàm số bậc hai. Đồ thị của hàm số bậc hai là một đường cong được gọi là parabol. Vị trí, hình dạng và kích thước của parabol phụ thuộc vào giá trị của a, b và c. Nếu a > 0, parabol có một điểm cực tiểu và bề lõm hướng lên trên; nếu a < 0, parabol có một điểm cực đại và bề lõm hướng xuống dưới. Điểm cực tiểu hoặc cực đại của parabol được gọi là đỉnh của parabol. Đồ thị giao trục hoành tại điểm có hoành độ là 0 và tung độ là c.
Các nghiệm của phương trình bậc hai (ax^2 + bx + c = 0) tương ứng với các nghiệm của hàm số (f(x) = ax^2 + bx + c) vì chúng là giá trị của x để f(x) = 0. Vị trí giao/tiếp điểm của đồ thị với trục hoành là nghiệm của phương trình.
Công Thức Viète
Công thức Viète cho biết quan hệ giữa các nghiệm của đa thức và các hệ số của nó. Trong trường hợp phương trình bậc hai, chúng được phát biểu như sau:
-
Nếu (x_1) và (x_2) là hai nghiệm của phương trình (ax^2 + bx + c = 0 (a ≠ 0)) thì: (begin{cases}x_1 + x_2 = S = -frac{b}{a}\x_1x_2 = P = frac{c}{a}end{cases})
-
Ngược lại, nếu (x_1) và (x_2) có tổng là S và tích là P thì (x_1) và (x_2) là 2 nghiệm của phương trình (x^2 - Sx + P = 0)
Các Trường Hợp Nhận Biết Đặc Biệt
Có một số trường hợp đặc biệt của phương trình bậc hai:
- Khi (a + b + c = 0), nghiệm của phương trình là: (x_1 = 1; x_2 = frac{c}{a}).
- Khi (a - b + c = 0), nghiệm của phương trình là: (x_1 = -1; x_2 = -frac{c}{a}).
- Khi ac < 0, tức a và c trái dấu nhau, phương trình luôn có 2 nghiệm phân biệt trái dấu.
Phép Tính Liên Quan
Hệ Phương Trình Online Phương Trình Bậc Hai Online Phương Trình Bậc Nhất Online
Phương trình bậc hai là một phần quan trọng của toán học. Hiểu và biết cách giải nhanh và chính xác phương trình này là một kỹ năng quan trọng. Với công cụ trực tuyến của HocTapHay.Com, bạn có thể giải phương trình bậc hai một cách dễ dàng và chính xác.
