Tìm hiểu về Quay lui trong lập trình

Ở trong bài học trước, chúng ta đã cùng nhau tìm hiểu về đệ quy. Ngày hôm nay, chúng ta sẽ tiếp tục khám phá khái niệm quay lui, một thuật toán gắn liền với đệ quy và được áp dụng rất nhiều trong các bài toán lập trình. Hiểu về quay lui sẽ giúp bạn nắm rõ logic của hàm đệ quy hơn.

Nội dung

Để tiếp thu bài học này một cách tốt nhất, bạn nên có kiến thức cơ bản về:

• Biến, kiểu dữ liệu, toán tử trong C++
• Câu điều kiện, vòng lặp, hàm trong C++
• Mảng trong C++
• Các kiến thức cần thiết để theo dõi khóa học
• Vector trong C++
• Đệ quy

Ở bài học ngày hôm nay, chúng ta sẽ cùng nhau tìm hiểu về:

• Khái niệm quay lui
• Cách áp dụng quay lui vào bài toán

Bài toán đặt ra

Bài toán được đưa ra là: Cho bàn cờ vua có kích thước n × n (4 ≤ n ≤ 10), các cột được đánh số từ 1 đến n theo chiều từ trái qua phải, các hàng được đánh số từ 1 đến n theo chiều từ trên xuống dưới. Hãy tìm cách đặt n quân hậu trên bàn cờ sao cho không có 2 quân hậu nào ở cùng một hàng, cột hay đường chéo.

Ví dụ:

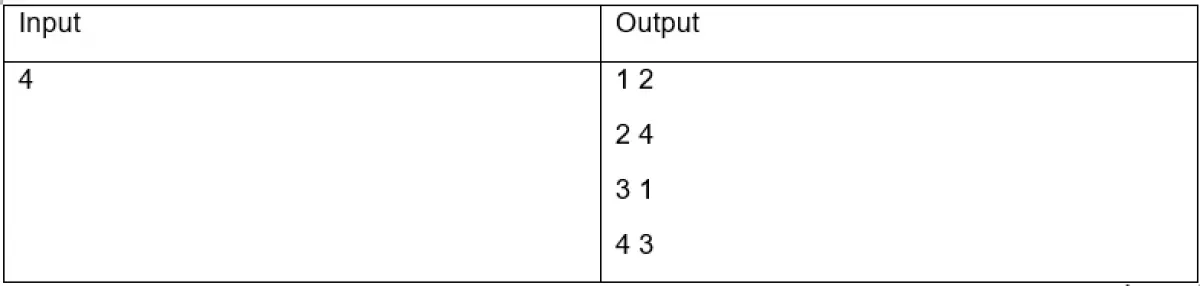
Giải thích ví dụ: Output trong ví dụ trên là vị trí các quân hậu trong bàn cờ thoả mãn yêu cầu. Dưới đây là hình minh hoạ cho vị trí các quân hậu.

Ý tưởng chung

Trước hết, cần phải nói rằng: Có thể có rất nhiều cách đặt quân hậu trên bàn cờ thoả mãn yêu cầu đề bài. Trên thực tế, với n = 8 thì có 12 cách xếp các quân hậu thoả mãn.

Bây giờ hãy quay lại với bài toán của chúng ta. Bài toán trên thực chất là một bài toán rất nổi tiếng trong Tin học đã được đặt ra vào những năm 1848. Trong các cách giải được đưa ra, cách phổ biến nhất đó chính là: Thử. Ta sẽ thử đặt 8 quân hậu vào các ô của bàn cờ sau đó kiểm tra xem liệu cách đặt đó có phù hợp hay không.

Vậy thì chúng ta nên thử như thế nào đây?

• Do các quân hậu không thể cùng nằm trên một hàng nên chắc chắn khi thử chúng ta sẽ phải đặt n quân hậu trên n hàng riêng biệt. Như vậy là đã đảm bảo điều kiện về hàng.
• Với mỗi hàng chúng ta sẽ đặt thử các quân hậu vào các vị trí trên hàng đó rồi tiến hành kiểm tra 2 điều kiện còn lại. Việc đặt thử này có thể tiến hành bằng việc dùng vòng lặp để duyệt qua tất cả các vị trí.
• Nếu gặp một trường hợp thoả mãn chúng ta có thể in ra kết quả và thoát chương trình.

Chi tiết về cách thử như thế nào hãy để ở phần sau. Bây giờ hãy xem xét một vấn đề: Chúng ta sẽ kiểm tra điều kiện không cùng cột và đường chéo như thế nào?

• Với điều kiện về cột, chúng ta sẽ sử dụng một mảng đánh dấu lại các cột đã có quân hậu. Nếu có một quân hậu được đặt vào cột đã được đánh dấu thì cách xếp hậu là không thoả mãn. Như vậy là ta đã kiểm tra được điều kiện về cột.
• Với đường chéo, mọi thứ sẽ phức tạp hơn. Ta nhận thấy, với mỗi quân hậu sẽ có 2 đường chéo để di chuyển. Chúng ta sẽ quy ước: đường chéo có chiều từ trái qua phải sẽ là "đường chéo chính", đường chéo có chiều từ phải qua trái sẽ là "đường chéo phụ".

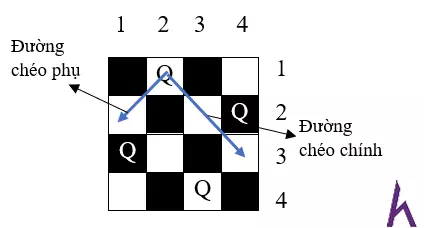
• Hãy cùng nhìn vào các ô ở đường chéo chính trong hình minh hoạ trên. Toạ độ các ô đó là (1, 2); (2, 3); (3, 4). Các bạn đã nhận ra điểm đặc biệt của các toạ độ kia chưa? Hiệu số giữa chỉ số hàng và cột là cố định với tất cả các ô thuộc cùng một đường chéo chính và mỗi đường chéo chính lại có một hiệu số riêng đặc trưng cho nó.
• Bây giờ hãy cùng nhìn vào đường chéo phụ trong hình minh hoạ. Toạ độ các ô trên đường chéo phụ là (1,2); (2, 1). Khác với đường chéo chính, tổng của chỉ số hàng và chỉ số cột của các ô thuộc cùng một đường chéo phụ là giống nhau và mỗi đường chéo phụ lại có một tổng riêng đặc trưng cho nó.
• Từ hai nhận xét trên, ta có thể dùng hai mảng đánh dấu lại hiệu của đường chéo chính và tổng của đường chéo phụ. Nếu quân hậu được đặt vào đường chéo đã được đánh dấu thì có nghĩa là không hợp lệ.

Triển khai ý tưởng

Chúng ta hiện tại sẽ có hai công việc chính:

• Đặt thử các quân hậu
• Kiểm tra tính hợp lệ của quân hậu được đặt vào

Với việc kiểm tra tính hợp lệ, chúng ta chỉ cần dùng 3 mảng đánh dấu một chiều với mục tiêu như đã trình bày ở trên. Việc này là không khó khăn. Bây giờ, vấn đề chính sẽ là làm sao để đặt thử các quân hậu.

Hãy thử hình dung luồng chạy của chương trình trong ví dụ ban đầu qua đoạn mã giả sau:

Xét hàng 1, đặt thử quân hậu tại vị trí cột 1. Phép đặt hợp lệ. Ta đánh dấu các cột, 2 đường chéo chứa quân hậu này. Chuyển qua xét hàng 2.
Xét hàng 2, đặt thử quân hậu tại vị trí cột 1. Phép đặt không hợp lệ do cùng cột với quân hậu đặt trước đó (hàng 1).
Xét hàng 2, đặt thử quân hậu tại vị trí cột 2. Phép đặt không hợp lệ do cùng đường chéo chính với quân hậu đặt trước đó (hàng 1).
Xét hàng 2, đặt thử quân hậu tại vị trí cột 3. Phép đặt hợp lệ. Ta đánh dấu các cột, 2 đường chéo chứa quân hậu này. Chuyển qua xét hàng 3.
Xét hàng 3, đặt thử quân hậu tại vị trí cột 1. Phép đặt không hợp lệ do cùng cột với quân hậu đặt trước đó (hàng 1).
Xét hàng 3, đặt thử quân hậu tại vị trí cột 2. Phép đặt không hợp lệ do cùng đường chéo phụ với quân hậu đặt trước đó (hàng 2).
Xét hàng 3, đặt thử quân hậu tại vị trí cột 3. Phép đặt không hợp lệ do cùng cột với quân hậu đặt trước đó (hàng 2).
Xét hàng 3, đặt thử quân hậu tại vị trí cột 4. Phép đặt không hợp lệ do cùng đường chéo chính với quân hậu đặt trước đó (hàng 2).
Do các phương án với hàng 3 đều không khả thi, quay lại xét hàng 2.
Xét hàng 2, xoá bỏ đánh dấu về cột và 2 đường chéo với cột 3 đang được chọn.
Xét hàng 2, đặt thử quân hậu tại vị trí cột 4 (do vị trí lần trước xét đang là 3). Phép đặt hợp lệ. Ta đánh dấu các cột, 2 đường chéo chứa quân hậu này. Chuyển qua xét hàng 3.
Quá trình tương tự
Khi ta xét đến hàng thứ 5 (hàng không có thật) có nghĩa là cả 4 hàng cần đặt quân hậu đều đã đặt thành công thì ta tin ra kết quả và dừng chương trình.

Nhìn vào quá trình vừa rồi, bạn có thấy quen không? Nếu chưa nhận ra được, hãy nhìn vào mô hình bên dưới của lời giải trên.

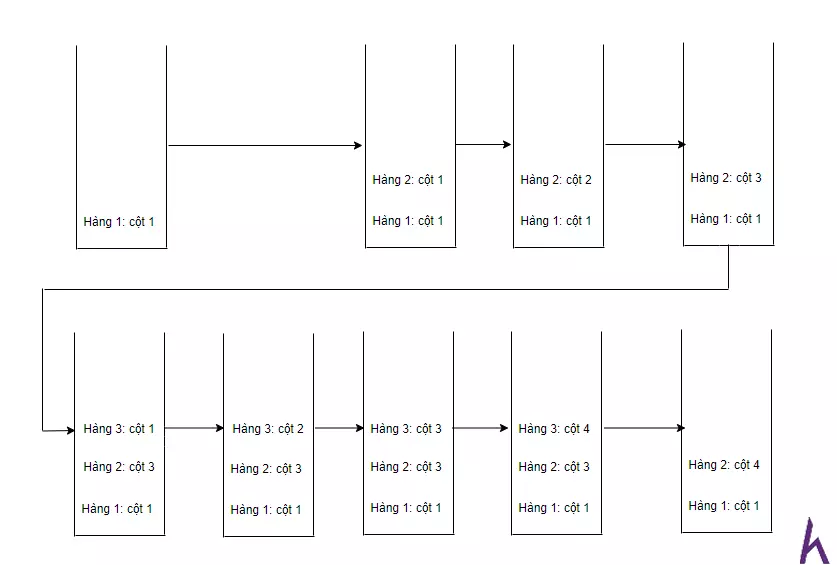
Bạn đã nhận ra mô hình này là của thứ gì chưa? Đó chính là mô hình của đệ quy mà ở bài trước mình đã giới thiệu. Phương pháp được sử dụng ở đây gọi là quay lui. Thế thì chính xác quay lui là gì?

Quay lui

Khái niệm

Quay lui là một thuật toán được thiết kế dựa trên đệ quy với ý tưởng: Tại mỗi bước, ta sẽ tìm một lời giải hợp lí cho bước đó rồi tiếp tục xét đến bước tiếp theo.

Thực chất, trong cuộc sống, có rất nhiều hành động chúng ta đang áp dụng chiến thuật quay lui. Giả sử, chúng ta biết nhà một người bạn chắc chắn nằm ở một trong những ngõ của con đường này nhưng chúng ta không biết chính xác ngõ nào. Có phải khi đó, ta sẽ đi vào từng ngõ. Với ngõ đó, ta sẽ đến từng nhà, hỏi thăm xem liệu đó có phải nhà chúng ta cần tìm không. Nếu đi đến cuối ngõ mà vẫn không tìm thấy, ta sẽ "quay lui" về đường chính để đi tìm ở một ngõ khác.

Ý tưởng

Sử dụng chiến lược quay lui để giải bài toán liệt kê các cấu hình. Mỗi cấu hình được xây dựng bằng cách xây dựng từng phần tử, mỗi phần tử được chọn bằng cách thử tất cả các khả năng.

Mô hình chung

Giả thiết cấu hình cần liệt kê có dạng x1, x2, x3, ..., xn. Khi đó thuật toán quay lui được thực hiện qua các bước sau:

• Xét tất cả các giá trị x1 có thể nhận, thử cho x1 nhận lần lượt các giá trị đó. Với mỗi giá trị thử cho x1 ta sẽ:
• Xét tất cả các giá trị x2 có thể nhận, thử cho x2 nhận lần lượt các giá trị đó. Với mỗi giá trị thử cho x2 ta sẽ xét các giá trị x3 có thể nhận và tiếp tục như vậy.
• Xét tất cả các giá trị xn có thể nhận, thử cho xn nhận lần lượt các giá trị đó. In ra cấu hình tìm được.

Giải quyết bài toán ban đầu

Vậy chính xác, bài toán ban đầu sẽ được code như thế nào với tư tưởng quay lui.

#include 
using namespace std;

const int MaxN = 1 + 1e5;
int n;
bool mark[3][MaxN];
vector res;

void Try(int row){
    if(row == n + 1){
        for(int i = 0 ; i < n ; ++i)
            cout << i + 1 << " " << res[i] << endl;
        exit(0); // Do chỉ cần in ra 1 đáp án nên ta sẽ thoát khỏi chương trình ngay tại đây.
        // Trên thực tế việc dùng hàm exit() tại đây là không tốt. Tuy nhiên, trong khuôn khổ của lập trình thi đấu, việc này là chấp nhận được.
    }
    for(int col = 1 ; col <= n ; ++col){
        // Do hiệu của chỉ số hàng và cột có thể âm nên ta cộng thêm n
        int mainDiagonal = row - col + n, subDiagonal = row + col;
        // mark[0][]: cột
        // mark[1][]: đường chéo chính
        // mark[2][]: đường chéo phụ
        if(mark[0][col] || mark[1][mainDiagonal] || mark[2][subDiagonal])
            continue;
        mark[0][col] = 1;
        mark[1][mainDiagonal] = 1;
        mark[2][subDiagonal] = 1;
        res.push_back(col);
        Try(row + 1);
        res.pop_back();
        mark[0][col] = 0;
        mark[1][mainDiagonal] = 0;
        mark[2][subDiagonal] = 0;
    }
}

int main(){
    freopen("CTDL.inp","r",stdin);
    freopen("CTDL.out","w",stdout);
    cin >> n;
    Try(1);
    return 0;
}

Vậy thì độ phức tạp của chương trình trên sẽ là bao nhiêu? Ta thấy, bản chất cách làm của ta là đi xét tất cả các trường hợp nên hàm đệ quy ở phía trên sẽ được gọi tối đa nn lần. Do đó, độ phức tạp chương trình là O(nn).

Chia sẻ bản thân

Chắc hẳn sẽ có rất nhiều bạn sau khi học xong hai bài đệ quy và quay lui sẽ cảm thấy khá "lú" và khó hiểu. Việc này là hết sức bình thường. Cơ chế hoạt động của hai thuật toán này đòi hỏi các bạn phải có thời gian gắn bó với lập trình nhất định và có khả năng tư duy trừu tượng khá tốt để có thể hiểu được nó.

Lời khuyên cho các bạn ở đây là gì? Hãy viết ra từng bước như những gì mình đã làm ở phần trên. Viết ra như vậy thì các bạn sẽ thấy rõ ràng việc chương trình của chúng ta sẽ chạy như thế nào.

Bản thân bài toán mình giải ở trên cũng không phải là một bài toán dễ. Mình đã mất 2 ngày áp dụng phương pháp viết ra từng câu lệnh như mình nêu ở trên để hiểu được bài toán này. Do vậy, nếu các bạn nghe qua 1 lần chưa hiểu, các bạn có thể nghe lại nhiều lần. Sau khi cảm thấy bản thân mình hiểu, hãy thử tự code bằng chính khả năng của mình. Không chỉ với bài học này mà với tất cả các bài học, mình tin khi các bạn có thể tự code được có nghĩa là các bạn thực sự hiểu những gì mình trình bày.

Một lưu ý nữa cho các bạn khi sử dụng đệ quy là nên đảm bảo ý tưởng đúng trước khi code do rất khó debug đệ quy với các bài toán phức tạp.

Kết luận

Qua bài này chúng ta đã nắm được về quay lui và cách áp dụng nó để giải các bài toán liệt kê cấu hình. Bài sau chúng ta sẽ bắt đầu tìm hiểu về sắp xếp. Cảm ơn các bạn đã theo dõi bài viết. Hãy để lại bình luận hoặc góp ý của mình để phát triển bài viết tốt hơn. Đừng quên "Luyện tập - Thử thách - Không ngại khó".

Thảo luận

Nếu bạn có bất kỳ khó khăn hay thắc mắc gì về khóa học, đừng ngần ngại đặt câu hỏi trong phần BÌNH LUẬN bên dưới hoặc trong mục HỎI & ĐÁP trên thư viện Howkteam.com để nhận được sự hỗ trợ từ cộng đồng.