Thuật toán quy hoạch động là một phương pháp rất phổ biến và mạnh mẽ trong giải quyết các bài toán khó khăn và đa dạng. Với mỗi bài toán, chúng ta cần suy nghĩ một cách sáng tạo để tìm ra lời giải. Không có một công thức chuẩn mực nào áp dụng được cho tất cả các bài toán. Tuy nhiên, quy hoạch động là một phương pháp được sử dụng phổ biến, và nếu bạn muốn đạt được kết quả tốt trong các cuộc thi, bạn cần trở thành một chuyên gia trong việc áp dụng thuật toán này.
Trong loạt bài viết "Quy hoạch động cho người mới bắt đầu", chúng ta sẽ khám phá sự phong phú và thú vị của quy hoạch động thông qua 6 phần, chia thành hai hướng tiếp cận khác nhau:
1. Khi nào thì dùng quy hoạch động
Việc xác định khi nào nên sử dụng quy hoạch động là một câu hỏi khó trả lời. Không có một công thức nào áp dụng cho tất cả các bài toán. Tuy nhiên, có một số tính chất tiêu biểu mà bạn có thể xem xét để áp dụng quy hoạch động. Dưới đây là hai tính chất nổi bật nhất:
- Bài toán có các bài toán con gối nhau (sử dụng công thức quy nạp): Sử dụng kết quả của các bài toán con để giải quyết bài toán lớn hơn (phương pháp chia để trị).
- Bài toán có cấu trúc con tối ưu.
2. Bài toán Fibonacci
Chúng ta có công thức truy hồi của số Fibonacci: F[n] = F[n-1] + F[n-2]. Hình sau minh họa quá trình tính hàm đệ quy Fibonacci khi n = 5:
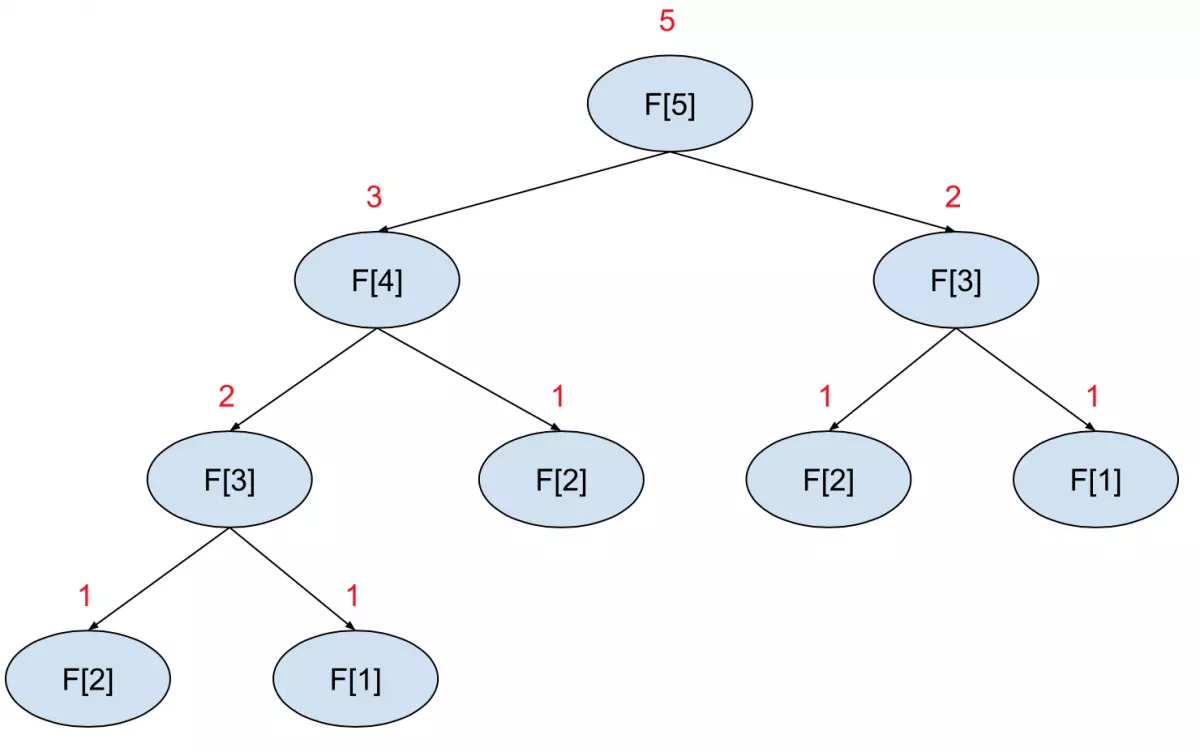
Khi tính F[5], chúng ta cần tính F[4] một lần, F[3] hai lần, F[2] ba lần và F[1] hai lần. Điều này cho thấy thuật toán đệ quy tính lại một bài toán nhiều lần, dẫn đến việc tốn thời gian và không hiệu quả.
Để giải quyết vấn đề này, ta có thể lưu lại kết quả của mỗi bài toán sau mỗi lần tính. Khi gặp lại bài toán đã được tính trước đó, ta chỉ cần trả về kết quả đã lưu, không cần tính lại. Phương pháp này được gọi là "quy hoạch động" và được thực hiện bằng phương pháp "đệ quy có nhớ". Đệ quy chỉ đơn giản là sử dụng hàm đệ quy để tính kết quả. Có nhớ chỉ đơn giản là lưu lại kết quả của bài toán vào một mảng để không cần tính lại nữa.
3. Cách chuyển từ nháp sang code đệ quy có nhớ
Khi mới học, ta nên nháp cẩn thận 4 bước để làm một bài toán quy hoạch động trước khi viết code. Các bước làm nháp bạn có thể tham khảo lại ở blog "Quy hoạch động cho người mới bắt đầu (Phần 1) - Sử dụng vòng lặp for cơ bản".
- Bước 1: Khai báo và khởi tạo mảng F: Kích thước và số chiều của mảng F sẽ tương ứng với số tham số mà ta đặt ý nghĩa trong hàm đệ quy.
- Bước 2: Khởi tạo giá trị của mảng F: Vì các giá trị này thể hiện bài toán đã được tính hay chưa, ta cần khởi tạo một giá trị mà không bao giờ xuất hiện trong kết quả (ví dụ: số âm). Có thể sử dụng lệnh
memset(F, 255, sizeof(F))để khởi tạo giá trị các phần tử trong mảng F bằng giá trị -1. - Bước 3: Triển khai code
4. Bài toán Frog 1
Link đề bài: Atcoder Educational DP Contest A - Frog 1
Yêu cầu đề bài: Xác định cách để chú ếch nhảy từ hòn đá (1) đến hòn đá (n) sao cho chi phí là nhỏ nhất.
Xác định các bước giải bài toán (làm ra nháp):
- Bước 1: Xác định ý nghĩa hàm đệ quy: Gọi dp(i) là chi phí nhỏ nhất để chú ếch nhảy khi đứng tại hòn đá (i), có nghĩa là các hòn đá từ (1) đến (i-1) đã được nhảy qua rồi.
- Bước 2: Xác định điều kiện dừng đệ quy: Nếu (i=n), trả về 0 (chú ếch đã đến hòn đá (n), không cần nhảy nữa)
- Bước 3: Xác định công thức tính đệ quy: Chú ếch đang đứng tại hòn đá thứ (i) có hai cách nhảy tiếp. Cách 1: Nhảy từ hòn đá (i) đến hòn đá (i+1). Chi phí nhỏ nhất để nhảy bằng cách này là dp(i+1) + abs(h[i]-h[i+1]). Cách 2: Nhảy từ hòn đá (i) đến hòn đá (i+2), với điều kiện (i) < (n-1) để tồn tại hòn đá (i+2). Chi phí nhỏ nhất để nhảy bằng cách này là dp(i+2) + abs(h[i]-h[i+2]).
- Bước 4: Xác định kết quả nằm ở đâu: Kết quả nằm ở dp(1), tức là khi chú ếch đứng tại vị trí (1).
5. Bài toán Xếp hàng mua vé
Link đề bài: Xếp hàng mua vé
Yêu cầu đề bài: Xác định những người cần rời hàng và nhờ người đứng trước mua hộ vé để tổng thời gian phục vụ bán vé là nhỏ nhất.
Xác định các bước giải bài toán:
- Bước 1: Xác định ý nghĩa hàm đệ quy: Gọi dp(i) là thời gian nhỏ nhất để mua vé khi đang mua cho người thứ (i). Nghĩa là người từ (1) đến (i-1) đã mua rồi.
- Bước 2: Xác định điều kiện dừng đệ quy: Nếu (i > n), trả về 0 (đã mua cho tất cả n người rồi, không cần mua nữa)
- Bước 3: Xác định công thức tính: Có hai trường hợp để người thứ (i) mua vé. Trường hợp 1: Người (i) tự mua vé của mình. Trong trường hợp này, mất thời gian là T[i], và người tiếp theo cần mua vé là người thứ (i+1). Công thức tính là dp(i+1) + T[i]. Trường hợp 2: Người (i) ra khỏi hàng và nhờ người (i+1) mua vé hộ. Trong trường hợp này, mất thời gian là R[i], và người tiếp theo cần mua vé là người thứ (i+2). Công thức tính là dp(i+2) + R[i].
- Bước 4: Xác định kết quả nằm ở đâu: Kết quả nằm ở dp(1), tức là thời gian nhỏ nhất để mua vé cho người đầu tiên.
Trên đây là một số bài toán quy hoạch động sử dụng đệ quy có nhớ với cách tiếp cận Top-down. Mỗi bài toán chỉ được tính duy nhất một lần.
Độ phức tạp của thuật toán quy hoạch động được tính bằng công thức:
Số bài toán * Chi phí chuyển trạng thái
Trong đó:
- Số bài toán là số phần tử trong mảng (F)
- Chi phí chuyển trạng thái là độ phức tạp khi triển khai công thức tính mỗi bài toán.
Ví dụ:
- Độ phức tạp của bài toán Fibonacci là O(n) (n bài toán, mỗi bài toán mất 1 phép tính để triển khai công thức).
- Độ phức tạp của bài toán Frog 1 là O(n) (n bài toán, mỗi bài toán mất 3 phép tính để triển khai công thức).
- Độ phức tạp của bài toán Xếp hàng mua vé cũng là O(n).
Như vậy, quy hoạch động là một phương pháp mạnh mẽ và linh hoạt trong giải quyết các bài toán. Bằng cách sử dụng cách tiếp cận đệ quy có nhớ, chúng ta có thể giải quyết các bài toán phức tạp một cách hiệu quả và linh hoạt.












