Tất cả những gì bạn cần biết về bài toán cái túi với C++

Giới thiệu

Bài toán cái túi là một bài toán cổ điển trong lĩnh vực lập trình. Trong bài toán này, chúng ta có một siêu thị với n đồ vật, mỗi đồ vật có trọng lượng và giá trị khác nhau. Một tên trộm đột nhập vào siêu thị và mang theo một cái túi có trọng lượng tối đa M. Bài toán đặt ra câu hỏi là chọn tập hợp các đồ vật sao cho tổng giá trị của chúng là lớn nhất.

Ý tưởng bài toán

Xây dựng Bảng DP (Programing Dynamic)

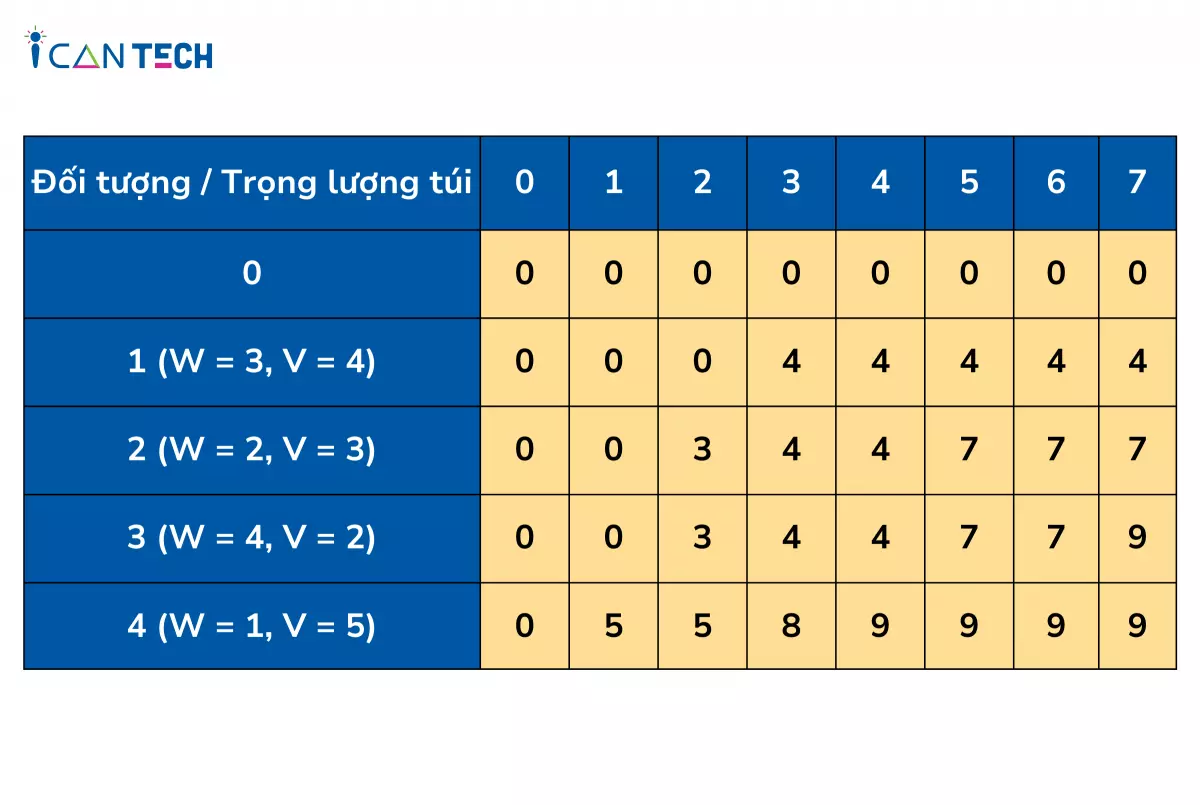
Chúng ta sử dụng một ma trận DP có kích thước (n+1) x (M+1) để giải quyết bài toán. DP[i][j] sẽ đại diện cho giá trị lớn nhất có thể đạt được với i đối tượng và túi có trọng lượng tối đa là j.

Viết công thức cập nhật DP

Chúng ta sử dụng công thức sau để cập nhật giá trị của DP[i][j]:

DP[i][j] = max(DP[i-1][j], DP[i-1][j - W[i]] + V[i])

Trong đó, W[i] là trọng lượng của đối tượng thứ i, và V[i] là giá trị của đối tượng thứ i.

Truy vết để xác định đồ vật được chọn

Bắt đầu từ DP[n][M] (góc phải dưới của ma trận), chúng ta có thể truy vết ngược lên để xác định các đồ vật được chọn.

Code bài toán cái túi C++

Dưới đây là một mẫu code giải bài toán cái túi bằng ngôn ngữ C++:

#include 
#include 

using namespace std;

const long long mod = 1e9 + 7;

void enter(int &n, int &M, vector &W, vector &V) {
    cin >> n >> M;
    W.resize(n + 1);
    V.resize(n + 1);
    for (int i = 1; i <= n; ++i)
        cin >> W[i] >> V[i];
}

void solution(int n, int M, const vector &W, const vector &V) {
    vector> DP(n + 1, vector(M + 1, 0));
    for (int i = 0; i <= n; ++i)
        DP[i][0] = 1;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= M; ++j) {
            DP[i][j] = DP[i - 1][j];
            if (j >= W[i]) {
                DP[i][j] = (DP[i][j] + DP[i - 1][j - W[i]]) % mod;
            }
        }
    }
    cout << DP[n][M];
}

int main() {
    int n, M;
    vector W, V;
    enter(n, M, W, V);
    solution(n, M, W, V);
    return 0;
}

Kết luận

Trên đây là cách giải bài toán cái túi thông qua ý tưởng và code bài toán. Hy vọng rằng bạn đã có thêm kiến thức về bài toán này và thuật toán giải bằng ngôn ngữ C++.

Cảm ơn bạn đã đọc bài viết, nếu bạn quan tâm đến học lập trình, hãy tham khảo ngay các khóa học lập trình tại ICANTECH.

Nguồn ảnh: ICANTECH.