Thuật toán tính nhanh nghịch đảo căn bậc 2: Một cái nhìn mới

Ảnh minh họa: Thuật toán tính nhanh nghịch đảo căn bậc 2.

Trong những năm 2002, 2003, khi mã nguồn của tựa game Quake 3 Arena được giới thiệu với mã nguồn mở, một thuật toán nhanh chóng tính toán nghịch đảo căn bậc 2 đã được khám phá. Được biết đến với tên gọi "Fast inverse square root", thuật toán này đã được sử dụng rộng rãi trong các phép tính vector của game 3D, như Quake 3. Mặc dù John Carmack, cha đẻ của dòng game Quake, được nhắc đến như người đã phổ biến hóa thuật toán này, nhưng thực tế là Gary Tarolli đã thực hiện các cài đặt đầu tiên trên máy tính SGI Indigo.

Việc tính căn bậc 2 của một số có nhiều phương pháp khác nhau. Dựa trên bài viết "Methods of computing square roots", ta có thể thấy các phương pháp này dựa trên việc lặp lại công thức để đạt được độ chính xác mong muốn.

Phương pháp Babylon

Một trong những phương pháp được sử dụng là phương pháp Babylon. Ví dụ, để tính căn bậc 2 của 125348, ta sẽ áp dụng phương pháp này:

Với x = 125348, chúng ta tính như sau:

Trên các máy tính hiện đại, đã có các bộ chỉ thị phần cứng riêng để tính căn bậc 2, nhưng vào những năm 90 của thế kỉ trước, phương pháp "Fast inverse square root" mang lại hiệu quả tính toán mà phần cứng chưa thể cung cấp.

Thuật toán cơ bản

Thuật toán cơ bản để tính nghịch đảo căn bậc 2 có thể được mô tả như sau:

1. Chuyển số sang dạng nguyên, tính xấp xỉ -1/2 log2(x).
2. Đổi lại số sang dạng số thực.
3. Xấp xỉ 1 lần nữa với phương pháp Newton.

Xấp xỉ Log2(x)

Biểu diễn số thực x dưới dạng tích của một số thực với lũy thừa của 2. Ta tính được 3 giá trị:

• Sx, là dấu, 0 nếu x > 0, là 1 nếu x < 0 (1 bit).
• Ex = ex + B là "biased exponent", với B = 127 là giá trị "exponent bias" (8 bits).
• Mx = mx × L, với L = 223 (23 bits).

Ta có:

Suy ra:

Vì m nằm trong đoạn từ 0 đến 1, ta có:

Vẽ lên đồ thị để thấy rõ hơn với σ = 0:

Người ta đã chứng minh được rằng, với σ ≈ 0.0430357, sai số tuyệt đối sẽ nhỏ nhất. Để đổi phần thập phân sang dạng số tự nhiên, ta có:

Suy ra:

Xấp xỉ 1 trên căn 2 x

Ta có:

Dựa theo công thức xấp xỉ log, ta có:

Suy ra:

Vì là một hằng số, ta có thể dễ dàng tính được phần Ix một cách dễ dàng.

Phương pháp Newton

Thuật toán sử dụng phương pháp Newton để tăng tính chính xác. Công thức như sau:

Tính đạo hàm ta có:

Theo công thức Newton, ta có:

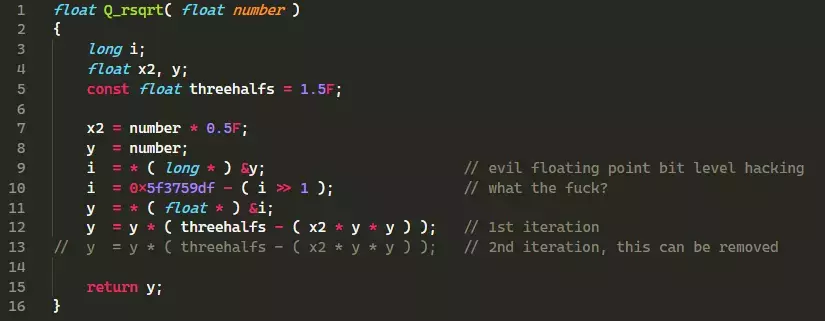
Trong phiên bản Quake 3, ngôn ngữ C, thuật toán được thể hiện như sau:

float Q_rsqrt(float number)
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y = number;
    i = *(long *)&y;
    i = 0x5f3759df - (i >> 1); // What the fuck?
    y = *(float *)&i;
    y = y * (threehalfs - (x2 * y * y));

    return y;
}

Dưới góc nhìn toán học thuần túy, tính toán trong lĩnh vực công nghệ luôn có những sự khác biệt. Tuy nhiên, những tính toán này dựa trên những biến đổi cơ bản và tự nhiên. Hy vọng bạn đã thấy bài viết này hữu ích.