Bài viết này sẽ hướng dẫn phương pháp tìm giao tuyến của hai mặt phẳng thông qua các ví dụ minh họa chi tiết. Chúng ta sẽ khám phá cách tìm điểm giao tuyến của hai mặt phẳng và áp dụng nó vào các bài toán cụ thể.
Phương pháp tìm giao tuyến của hai mặt phẳng
Giao tuyến là đường thẳng chung của hai mặt phẳng, có nghĩa giao tuyến là đường thẳng vừa thuộc mặt phẳng này vừa thuộc mặt phẳng kia. Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung thuộc cả hai mặt phẳng, sau đó nối hai điểm chung đó để được đường giao tuyến cần tìm. Điểm chung thứ nhất thường dễ tìm, điểm chung còn lại ta phải tìm hai đường thẳng lần lượt thuộc hai mặt phẳng, đồng thời cùng thuộc một mặt phẳng thứ ba mà chúng không song song với nhau. Giao điểm của hai đường thẳng đó chính là điểm chung thứ hai.
Ví dụ minh họa
Ví dụ 1: Tìm giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$
Cho tứ giác $ABCD$ sao cho các cạnh đối không song song với nhau. Lấy một điểm $S$ không thuộc mặt phẳng $(ABCD)$. Để tìm giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$, chúng ta sẽ tìm điểm chung của hai mặt phẳng và nối chúng để được đường giao tuyến.
- Gọi $O$ là giao điểm của $AC$ và $BD$ trong mặt phẳng $(ABCD)$.
- Vì $O$ thuộc cả $(SAC)$ và $(SBD)$, nên ta có điểm chung thứ nhất là $O$.
- Để tìm điểm chung thứ hai, chúng ta cần tìm hai đường thẳng thuộc từng mặt phẳng và cùng thuộc một mặt phẳng thứ ba mà chúng không song song với nhau. Tại đây, chúng ta có $O$ thuộc $(SAC)$, nên chúng ta có thể lấy $AB$ là đường thẳng thuộc $(SAC)$. Tương tự, chúng ta có thể lấy $CD$ là đường thẳng thuộc $(SBD)$.
- Nối điểm chung của $AB$ và $CD$, ta được đường giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$, ký hiệu là $SO$.
Ví dụ 2: Tìm giao tuyến của hai mặt phẳng $(IBC)$ và $(JAD)$
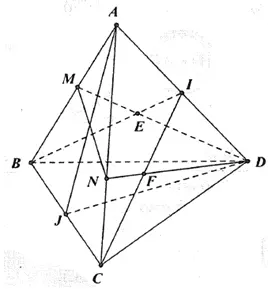
Cho tứ diện $ABCD$. Gọi $I$ và $J$ lần lượt là trung điểm của các cạnh $AD$ và $BC$. Chúng ta sẽ tìm giao tuyến của hai mặt phẳng $(IBC)$ và $(JAD)$ bằng cách tìm điểm chung của hai mặt phẳng.

- Gọi $E$ là điểm giao điểm của $BI$ và $DM$ trong mặt phẳng $(ABCD)$. Vì $E$ thuộc cả $(IBC)$ và $(JAD)$, nên ta có điểm chung thứ nhất là $E$.
- Để tìm điểm chung thứ hai, chúng ta cần tìm hai đường thẳng thuộc từng mặt phẳng và cùng thuộc một mặt phẳng thứ ba mà chúng không song song với nhau. Tại đây, chúng ta có $E$ thuộc $(IBC)$, nên chúng ta có thể lấy $AD$ là đường thẳng thuộc $(IBC)$. Tương tự, chúng ta có thể lấy $BC$ là đường thẳng thuộc $(JAD)$.
- Nối điểm chung của $AD$ và $BC$, ta được đường giao tuyến của hai mặt phẳng $(IBC)$ và $(JAD)$, ký hiệu là $EI$.
Ví dụ 3: Tìm giao tuyến của hai mặt phẳng $(MNI)$ và $(BCD)$
Cho tứ diện $ABCD$. Lấy điểm $M$ thuộc cạnh $AB$, $N$ thuộc cạnh $AC$ sao cho $MN$ cắt $BC$. Gọi $I$ là điểm bên trong tam giác $BCD$. Chúng ta sẽ tìm giao tuyến của hai mặt phẳng $(MNI)$ và $(BCD)$ bằng cách tìm điểm chung của hai mặt phẳng.
- Gọi $H$ là điểm giao điểm của $MN$ và $BC$ trong mặt phẳng $(ABCD)$. Vì $H$ thuộc cả $(MNI)$ và $(BCD)$, nên ta có điểm chung thứ nhất là $H$.
- Để tìm điểm chung thứ hai, chúng ta cần tìm hai đường thẳng thuộc từng mặt phẳng và cùng thuộc một mặt phẳng thứ ba mà chúng không song song với nhau. Tại đây, chúng ta có $H$ thuộc $(MNI)$, nên chúng ta có thể lấy $AD$ là đường thẳng thuộc $(MNI)$. Tương tự, chúng ta có thể lấy $BC$ là đường thẳng thuộc $(BCD)$.
- Nối điểm chung của $AD$ và $BC$, ta được đường giao tuyến của hai mặt phẳng $(MNI)$ và $(BCD)$, ký hiệu là $HI$.
Ví dụ 4: Tìm giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang có $AB$ song song với $CD$. Lấy $M$ thuộc cạnh $SC$. Chúng ta sẽ tìm giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$ bằng cách tìm điểm chung của hai mặt phẳng.

- Gọi $O$ là điểm giao điểm của $AC$ và $BD$ trong mặt phẳng $(ABCD)$. Vì $O$ thuộc cả $(SAC)$ và $(SBD)$, nên ta có điểm chung thứ nhất là $O$.
- Để tìm điểm chung thứ hai, chúng ta cần tìm hai đường thẳng thuộc từng mặt phẳng và cùng thuộc một mặt phẳng thứ ba mà chúng không song song với nhau. Tại đây, chúng ta có $O$ thuộc $(SAC)$, nên chúng ta có thể lấy $AB$ là đường thẳng thuộc $(SAC)$. Tương tự, chúng ta có thể lấy $CD$ là đường thẳng thuộc $(SBD)$.
- Nối điểm chung của $AB$ và $CD$, ta được đường giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$, ký hiệu là $SO$.
Ví dụ 5: Tìm giao tuyến của hai mặt phẳng $(MNP)$ và $(SAB)$
Cho hình chóp $S.ABCD$ đáy là hình bình hành tâm $O$. Gọi $M, N, P$ lần lượt là trung điểm các cạnh $BC, CD, SA$. Chúng ta sẽ tìm giao tuyến của hai mặt phẳng $(MNP)$ và $(SAB)$ bằng cách tìm điểm chung của hai mặt phẳng.

- Gọi $F$ là điểm giao điểm của $MN$ và $AB$ trong mặt phẳng $(ABCD)$. Vì $F$ thuộc cả $(MNP)$ và $(SAB)$, nên ta có điểm chung thứ nhất là $F$.
- Để tìm điểm chung thứ hai, chúng ta cần tìm hai đường thẳng thuộc từng mặt phẳng và cùng thuộc một mặt phẳng thứ ba mà chúng không song song với nhau. Tại đây, chúng ta có $F$ thuộc $(MNP)$, nên chúng ta có thể lấy $BC$ là đường thẳng thuộc $(MNP)$. Tương tự, chúng ta có thể lấy $CD$ là đường thẳng thuộc $(SAB)$.
- Nối điểm chung của $BC$ và $CD$, ta được đường giao tuyến của hai mặt phẳng $(MNP)$ và $(SAB)$, ký hiệu là $PF$.
Ví dụ 6: Tìm giao tuyến của hai mặt phẳng $(MNI)$ và $(ABC)$
Cho tứ diện $ABCD$. Lấy $I$ thuộc cạnh $AB$ và $J$ là điểm trong tam giác $BCD$. Chúng ta sẽ tìm giao tuyến của hai mặt phẳng $(MNI)$ và $(ABC)$ bằng cách tìm điểm chung của hai mặt phẳng.

- Gọi $K$ là điểm giao điểm của $NI$ và $BJ$ trong mặt phẳng $(ABCD)$. Vì $K$ thuộc cả $(MNI)$ và $(ABC)$, nên ta có điểm chung thứ nhất là $K$.
- Để tìm điểm chung thứ hai, chúng ta cần tìm hai đường thẳng thuộc từng mặt phẳng và cùng thuộc một mặt phẳng thứ ba mà chúng không song song với nhau. Tại đây, chúng ta có $K$ thuộc $(MNI)$, nên chúng ta có thể lấy $AD$ là đường thẳng thuộc $(MNI)$. Tương tự, chúng ta có thể lấy $BC$ là đường thẳng thuộc $(ABC)$.
- Nối điểm chung của $AD$ và $BC$, ta được đường giao tuyến của hai mặt phẳng $(MNI)$ và $(ABC)$, ký hiệu là $KI$.
Ví dụ 7: Tìm giao tuyến của hai mặt phẳng $(AMN)$ và $(BCD)$
Cho tứ diện $ABCD$. Lấy $M$ là một điểm nằm bên trong tam giác $ABD$, $N$ là một điểm nằm bên trong tam giác $ACD$. Chúng ta sẽ tìm giao tuyến của hai mặt phẳng $(AMN)$ và $(BCD)$ bằng cách tìm điểm chung của hai mặt phẳng.

- Gọi $E$ là điểm giao điểm của $AM$ và $AD$ trong mặt phẳng $(ABCD)$. Vì $E$ thuộc cả $(AMN)$ và $(BCD)$, nên ta có điểm chung thứ nhất là $E$.
- Để tìm điểm chung thứ hai, chúng ta cần tìm hai đường thẳng thuộc từng mặt phẳng và cùng thuộc một mặt phẳng thứ ba mà chúng không song song với nhau. Tại đây, chúng ta có $E$ thuộc $(AMN)$, nên chúng ta có thể lấy $BC$ là đường thẳng thuộc $(AMN)$. Tương tự, chúng ta có thể lấy $CD$ là đường thẳng thuộc $(BCD)$.
- Nối điểm chung của $BC$ và $CD$, ta được đường giao tuyến của hai mặt phẳng $(AMN)$ và $(BCD)$, ký hiệu là $EF$.
Ví dụ 8: Tìm giao tuyến của hai mặt phẳng $(IJK)$ và các mặt của tứ diện
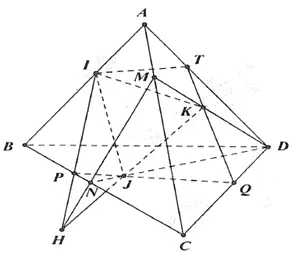
Cho tứ diện $ABCD$. Lấy $I$ trên cạnh $AB$, $J$ bên trong tam giác $BCD$ và $K$ bên trong tam giác $ACD$. Chúng ta sẽ tìm giao tuyến của mặt phẳng $(IJK)$ với các mặt của tứ diện bằng cách tìm điểm chung của mặt phẳng.

- Gọi $M$ là điểm giao điểm của $DK$ và $AC$ trong mặt phẳng $(ABCD)$. Vì $M$ thuộc cả $(IJK)$ và các mặt của tứ diện, nên ta có điểm chung thứ nhất là $M$.
- Để tìm điểm chung thứ hai, chúng ta cần tìm hai đường thẳng thuộc từng mặt phẳng và cùng thuộc một mặt phẳng thứ ba mà chúng không song song với nhau. Tại đây, chúng ta có $M$ thuộc $(IJK)$, nên chúng ta có thể lấy $BC$ là đường thẳng thuộc $(IJK)$.
- Đường giao tuyến của mặt phẳng $(IJK)$ với các mặt của tứ diện là đường thẳng $IM$.
Đó là cách tìm giao tuyến của hai mặt phẳng thông qua các ví dụ minh họa chi tiết. Việc tìm điểm chung của hai mặt phẳng sẽ giúp chúng ta hiểu rõ hơn về quan hệ giữa các mặt phẳng trong không gian ba chiều.












