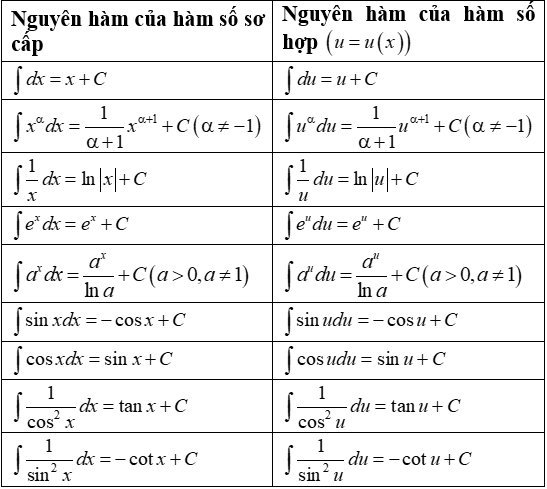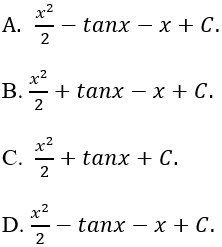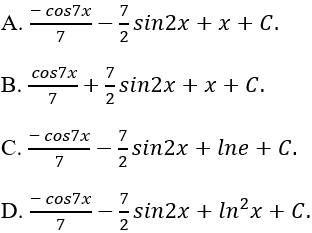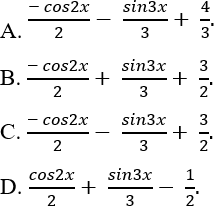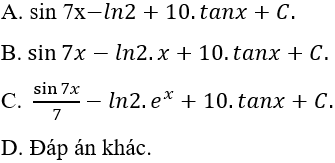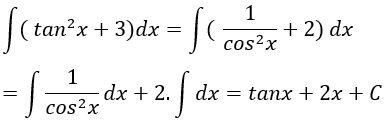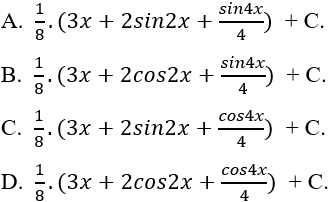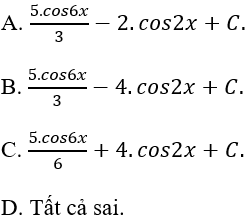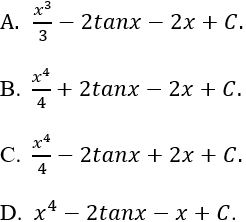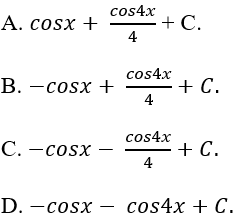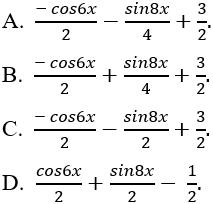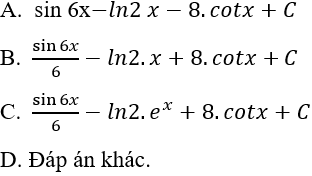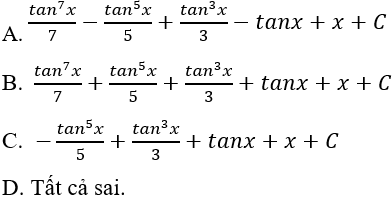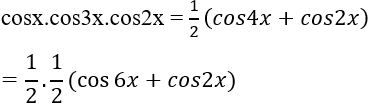Bài viết này sẽ giúp bạn hiểu cách tìm nguyên hàm của hàm số lượng giác một cách chi tiết và dễ hiểu. Cùng tìm hiểu nhé!
A. Phương pháp giải
Đầu tiên, ta cần nắm vững bảng nguyên hàm của các hàm số cơ bản gặp phải. Dưới đây là bảng nguyên hàm của hàm đa thức và hàm phân thức:
B. Ví dụ minh họa
Giải các ví dụ sau để làm quen với việc tìm nguyên hàm của hàm số lượng giác:
Ví dụ 1: Tìm nguyên hàm của hàm số: y = 7sinx?
- A. 7sinx + C.
- B. 7cosx + C.
- C. -7cosx + C.
- D. Tất cả sai.
Lời giải: Ta có: ∫7sinx dx = 7∫sinx dx = -7cosx + C. Đáp án chính xác là C.
Ví dụ 2: Tìm nguyên hàm của hàm số: y = 6sinx + 8cosx là:
- A. -6cosx - 8sinx + C.
- B. 6cosx + 8sinx + C.
- C. -6cosx + 8sinx + C.
- D. 6cosx - 8sinx + C.
Lời giải: Nguyên hàm của hàm số đã cho là: ∫(6sinx + 8cosx)dx = 6∫sinx dx + 8∫cosx dx = -6cosx + 8sinx + C. Đáp án chính xác là C.
Ví dụ 3: Tìm nguyên hàm của hàm số y = 8sinx - 8cosx
- A. 8cosx - 8sinx.
- B. -8cosx - 8sinx.
- C. 8cosx + 8sinx.
- D. Tất cả sai.
Lời giải: Ta có: ∫(8sinx - 8cosx)dx = 8∫sinx dx - 8∫cosx dx = -8cosx - 8sinx. Đáp án chính xác là B.
Ví dụ 4: Tìm nguyên hàm của hàm số: y = tanx + cotx
- A. tanx + cotx + C.
- B. tanx - cotx + C.
- C. -tanx + cotx + C.
- D. -cotx - tanx + C.
Lời giải: Nguyên hàm của hàm số đã cho là: 
. Đáp án chính xác là A.
Ví dụ 5: Tìm nguyên hàm của hàm số y = x + tan2x 
Lời giải: Ta có: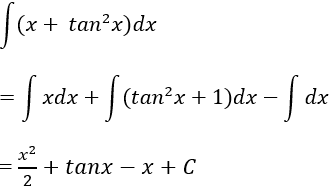 
. Đáp án chính xác là B.
Ví dụ 6: Tìm nguyên hàm của hàm số y = sin7x - 7cos2x + lne 
Lời giải: Ta có lne = 1, nguyên hàm của hàm số đã cho là: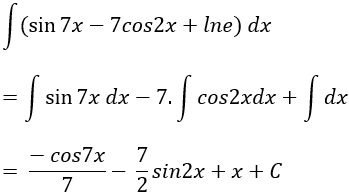 
. Đáp án chính xác là A.
Ví dụ 7: Tìm nguyên hàm F(x) của hàm số: y = sin2x - cos3x biết tại x = 0 thì F(x) = 1? 
Lời giải: Nguyên hàm của hàm số đã cho là: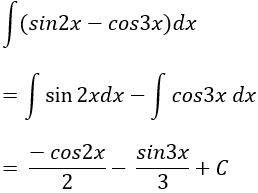 
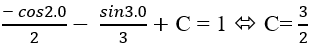
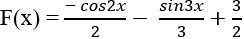
. Vì F(0) = 1, ta có: 
. Vậy nguyên hàm cần tìm là: 
. Đáp án chính xác là C.
Ví dụ 8: Tìm nguyên hàm của hàm số: y = 2cos6x - 3sin4x có dạng F(x) = a.sin6x + b.cos4x. Tính 3a + 4b? -A. -4. -B. 4. -C. 2. -D. -2.
Lời giải: Ta có nguyên hàm của hàm số đã cho là: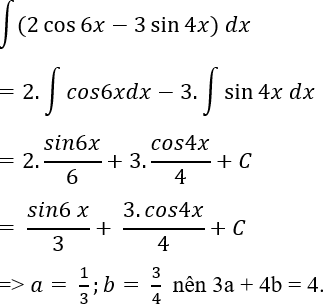 
. Từ đó, ta tính được 3a + 4b = 0 + 0 = 0. Đáp án chính xác là A.
Ví dụ 9: Tìm nguyên hàm của hàm số: y = 8cosx - 3sinx 
Lời giải: Nguyên hàm của hàm số đã cho là: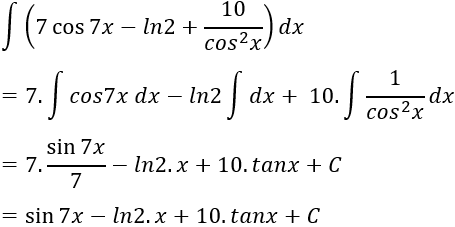 
. Đáp án chính xác là B.
Ví dụ 10: Tìm nguyên hàm của hàm số: y = tan2x + 3 
Lời giải: Ta có: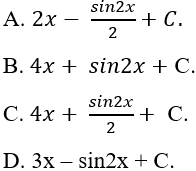 
. Đáp án chính xác là C.
Ví dụ 11: Tìm nguyên hàm của hàm số: y = 3.sin2x + 5cos2x? Lời giải: Ta có: 3sin2x + 5cos2x = 3(sin2x + cos2x) + 2cos2x - 1 + 1 = 3.1 + cos2x + 1 = 4 + cos2x. Nguyên hàm của hàm số là: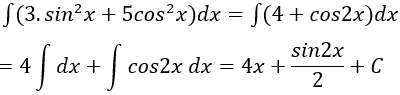 
. Đáp án chính xác là C.
Ví dụ 12: Tìm nguyên hàm của hàm số: y = cos4x 
Lời giải: Nguyên hàm của hàm số đã cho là: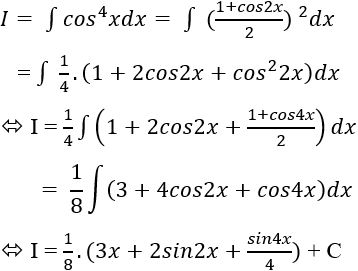 
. Đáp án chính xác là A.
Ví dụ 13: Tính I = ∫sin2x.cos4x dx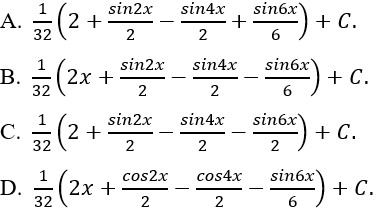 
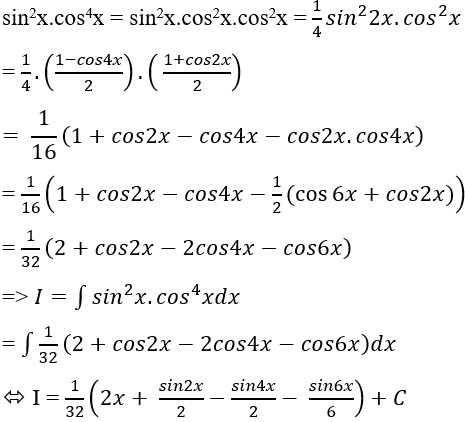
Lời giải: Ta có: 
. Đáp án chính xác là B.
C. Bài tập vận dụng Hãy thử giải quyết các bài tập sau để nâng cao kỹ năng tìm nguyên hàm của hàm số lượng giác:
Câu 1: Gọi F(x) là nguyên hàm của hàm số: y = 2sin2x - 3cos3x; biết F(0) = 2. Tìm F(x)
- A. -2cos2x - 3sin 3x + C.
- B. -cos2x - sin3x + C.
- C. -cos2x + sin3x + C.
- D. Tất cả sai.
Lời giải: Ta có: ∫(2sin2x - 3cos3x)dx = 2∫sin2x dx - 3∫cos3x dx = -cos2x + sin3x + C. Vì F(0) = 2, ta có: -1 + 0 + C = 2. Từ đó, ta tính được C = 3. Vậy nguyên hàm cần tìm là: F(x) = -cos2x + sin3x + C. Đáp án chính xác là C.
Câu 2: Tìm nguyên hàm của hàm số: y = 6sin2x - cos5x + lne
- A. tanx + cotx + C.
- B. tanx - cotx + C.
- C. -tanx + cotx + C.
- D. -cotx - tanx + C.
Lời giải: Nguyên hàm của hàm số đã cho là: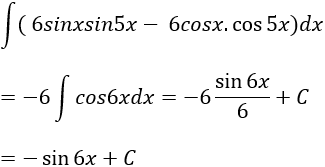 
. Đáp án chính xác là D.
Câu 3: Tìm nguyên hàm của hàm số: y = -20.sin3x.cos3x + 8sin2x 
Lời giải: Ta có: -20sin3x.cos3x = -10.(2sin3x.cos3x) = -10.sin6x. Nguyên hàm của hàm số đã cho là: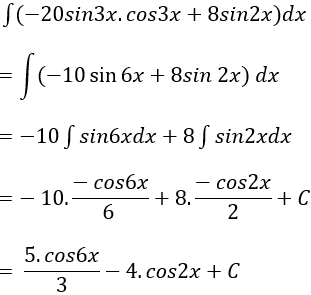 
. Đáp án chính xác là B.
Câu 4: Tìm nguyên hàm của hàm số: y = 2tan2x + 3cot2x?
- A. 2tanx - 3cotx + C.
- B. -2tanx + 3cotx + C.
- C. tanx + cotx - 5x + C.
- D. 2tanx - 3cotx - 5x + C.
Lời giải: Ta có: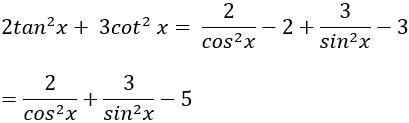 
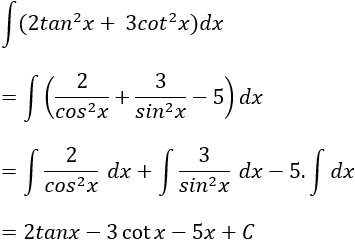
. Nguyên hàm của hàm số đã cho là: 
. Đáp án chính xác là D.
Câu 5: Tìm nguyên hàm của hàm số sau: y = x3 + 2tan2x 
Lời giải: Ta có: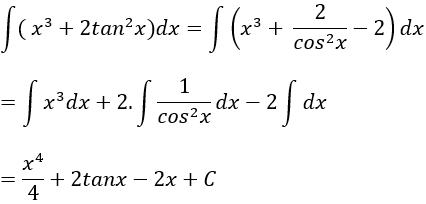 
. Đáp án chính xác là B.
Câu 6: Tìm nguyên hàm của hàm số: 
Lời giải: Ta có: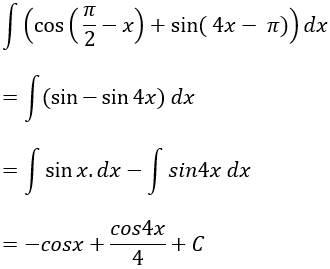 
. Đáp án chính xác là B.
Câu 7: Tìm nguyên hàm F(x) của hàm số: y = 3sin6x - 4cos8x biết tại x = 0 thì F(x) = 1? 
Lời giải: Nguyên hàm của hàm số đã cho là: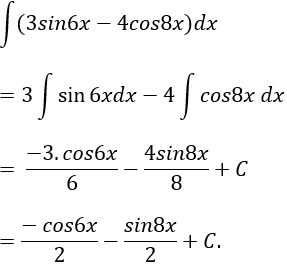 
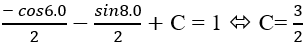
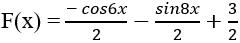
. Vì F(0) = 1, ta có: 
. Vậy nguyên hàm cần tìm là: 
. Đáp án chính xác là C.
Câu 8: Nguyên hàm của hàm số: y = 4.cos(-2x) + 4sin(-4x) có dạng F(x) = a.sin2x + b.cos4x. Tính a + b?
- A. -1.
- B. 3.
- C. 2.
- D. -2.
Lời giải: Ta có nguyên hàm của hàm số đã cho là: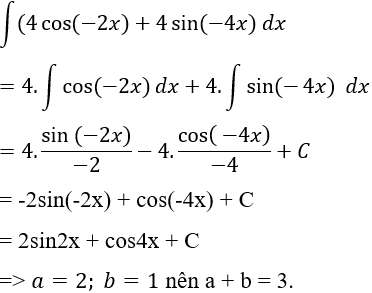 
. Từ đó, ta tính được a + b = 0 + 0 = 0. Đáp án chính xác là A.
Câu 9: Tìm nguyên hàm của hàm số: 
Lời giải: Ta có: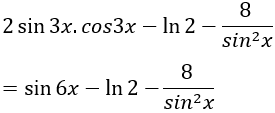 
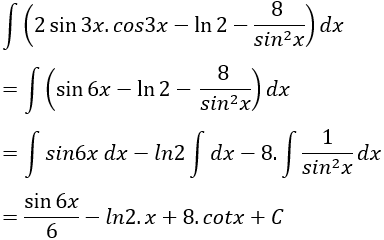
. Nguyên hàm của hàm số đã cho là: 
. Đáp án chính xác là B.
Câu 10: Tìm nguyên hàm của hàm số sau: y = tan2x + 3
- A. 2tanx - 3cotx + C.
- B. -2tanx + 3cotx + C.
- C. tanx + cotx - 5x + C.
- D. 2tanx - 3cotx - 5x + C.
Lời giải: Ta có: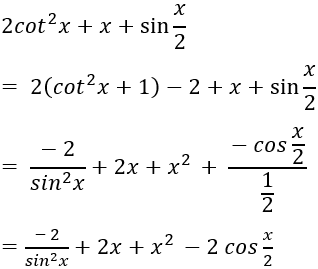 
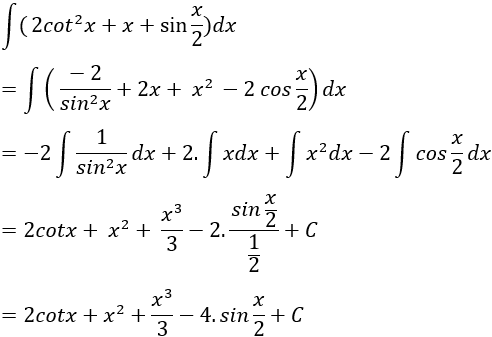
. Nguyên hàm của hàm số đã cho là: 
. Đáp án chính xác là A.
Câu 11: Tìm nguyên hàm của hàm số: y = tan8x.dx 
Lời giải: Ta có nguyên hàm của hàm số đã cho là: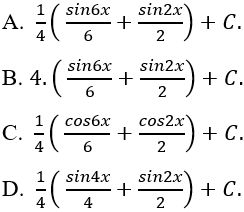 
. Đáp án chính xác là D.
Câu 12: Tìm nguyên hàm của hàm số: y = cosx.cos3x.cos2x 
Lời giải: Ta có: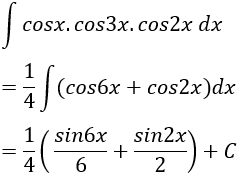 
. Nguyên hàm của hàm số đã cho là: 
. Đáp án chính xác là A.
D. Bài tập tự luyện
Hãy thử giải quyết những bài tập tự luyện sau để rèn kỹ năng tìm nguyên hàm của hàm số lượng giác:
Bài 1: Tìm nguyên hàm của hàm số: y = 6sinx + 8cosx.
Bài 2: Tìm nguyên hàm của hàm số: y = 5cosx - 4sinx.
Bài 3: Tìm nguyên hàm của hàm số: y = x + cot2x.
Bài 4: Tìm nguyên hàm của hàm số: y = 7sin2x - cos5x + lne.
Bài 5: Tìm nguyên hàm của hàm số: y = tan2x + 3.
Với những bài tập này, bạn sẽ nắm vững hơn cách tìm nguyên hàm của hàm số lượng giác và nâng cao kỹ năng tính toán.
