Tìm hiểu thuật toán Dijkstra
Thuật toán Dijkstra là một thuật toán tìm kiếm đường đi ngắn nhất rất phổ biến trong lĩnh vực tìm kiếm đường đi trên đồ thị. Trong bài học trước, chúng ta đã tìm hiểu về thuật toán Floyd-Warshall trong tìm kiếm đường đi ngắn nhất trên đồ thị. Hôm nay, chúng ta sẽ cùng nhau tìm hiểu về thuật toán Dijkstra, một thuật toán được coi là phổ biến nhất trong tìm kiếm đường đi ngắn nhất. Hãy cùng bắt đầu bài học!
Giới thiệu về thuật toán Dijkstra
Trước khi tiếp thu bài học này, để hiểu rõ hơn về thuật toán Dijkstra, bạn cần có những kiến thức cơ bản sau:
- Các kiến thức cần thiết để theo dõi khóa học
- Đồ thị và cây
- BFS và DFS
- Priority Queue
- Thuật toán Floyd-Warshall
Trong bài học ngày hôm nay, chúng ta sẽ tìm hiểu về thuật toán Dijkstra.
Bài toán đặt ra
Chúng ta có một bài toán như sau:
Cho một đồ thị có hướng gồm đỉnh (đánh số từ 1 đến n), cạnh có hướng và có trọng số là số nguyên không âm. Cho một đỉnh s, hãy tìm độ dài đường đi ngắn nhất từ đỉnh s đến tất cả các đỉnh còn lại trên đồ thị. Nếu không tồn tại đường đi giữa hai đỉnh, in ra -1.
Input:
- Dòng 1: Gồm 3 số nguyên n, m, s lần lượt thể hiện số đỉnh của đồ thị, số cạnh của đồ thị và đỉnh yêu cầu 1 ≤ n, m ≤ 10^5, 1 ≤ s ≤ n
- Dòng 2_m+1: Mỗi dòng gồm 3 số nguyên u, v, w thể hiện một cạnh có hướng nối từ đỉnh u đến đỉnh v và có trọng số w (1 ≤ u,v ≤ n, 0 ≤ w ≤ 10^9)
Output:
- Gồm m dòng, dòng thứ i thể hiện độ dài đường đi ngắn nhất từ đỉnh s đến đỉnh i
Ví dụ:
Input:
7 8 1
1 2 4
1 3 5
1 4 2
4 2 1
4 6 4
3 5 3
6 5 1
1 5 8Output:
0
3
5
2
7
6
-1Ý tưởng của thuật toán Dijkstra
Thuật toán Dijkstra chọn ra một đỉnh u mà ta biết chắc chắn đường đi từ s đến u là đường đi ngắn nhất. Sau đó, ta xét tất cả các đỉnh v mà có cạnh liên kết trực tiếp từ u và tối ưu đường đi từ s đến v dựa trên đường đi từ s đến u.
Cách cài đặt
Trước hết, để tiện trong việc thể hiện một cạnh, chúng ta sử dụng vector với kiểu dữ liệu pair
Ví dụ:
#include
using namespace std;
int main(){
pair myPair[2]; // Có 2 cách khởi tạo pair
myPair[0] = make_pair(1, 2);
myPair[1] = {2, 3};
cout << myPair[0].first << " " << myPair[0].second << endl; // Kết quả: 1 2
return 0;
} Ta sẽ cần khởi tạo hai mảng với ý nghĩa như sau:
- dist[u]: độ dài đường đi ngắn nhất từ đỉnh nguồn s đến đỉnh u. Ban đầu dist[u] = ∞ với mọi u, riêng dist[s] = 0
- mark[u]: đánh dấu đỉnh u đã được xét hay chưa. Ban đầu các phần tử trong mảng có giá trị false
==> Trong ví dụ trên, ta thấy có tối đa 10^5 cạnh, mỗi cạnh có trọng số không quá 10^9 nên độ dài một đường đi không quá 10^14. Giá trị ∞ khi này có thể là bất cứ giá trị nào lớn hơn hoặc bằng 10^14.
Thuật toán sẽ diễn ra như sau:
- Chọn một đỉnh u mà ta biết chắc chắn đường đi từ s đến u là đường đi ngắn nhất
- Với đỉnh u mà ta đã chọn ở trên, ta sẽ xét tất cả các đỉnh v mà có cạnh liên kết trực tiếp từ u. Nếu dist[u] + độ dài cạnh u-v < dist[v], hãy có nghĩa là độ dài đường đi từ đỉnh s đến đỉnh v thông qua đỉnh u ngắn hơn đường đi hiện tại từ đỉnh s đến đỉnh v thì ta sẽ cập nhật lại dist[v] = dist[u] + độ dài cạnh u-v
- Khi xét xong tất cả các đỉnh có cạnh liên kết trực tiếp từ u, đánh dấu mark[u] = true tức là đỉnh u đã xử lý xong.
Minh hoạ
Mình sẽ minh họa thuật toán bằng một đồ thị cơ bản sau với đỉnh nguồn là đỉnh 1:
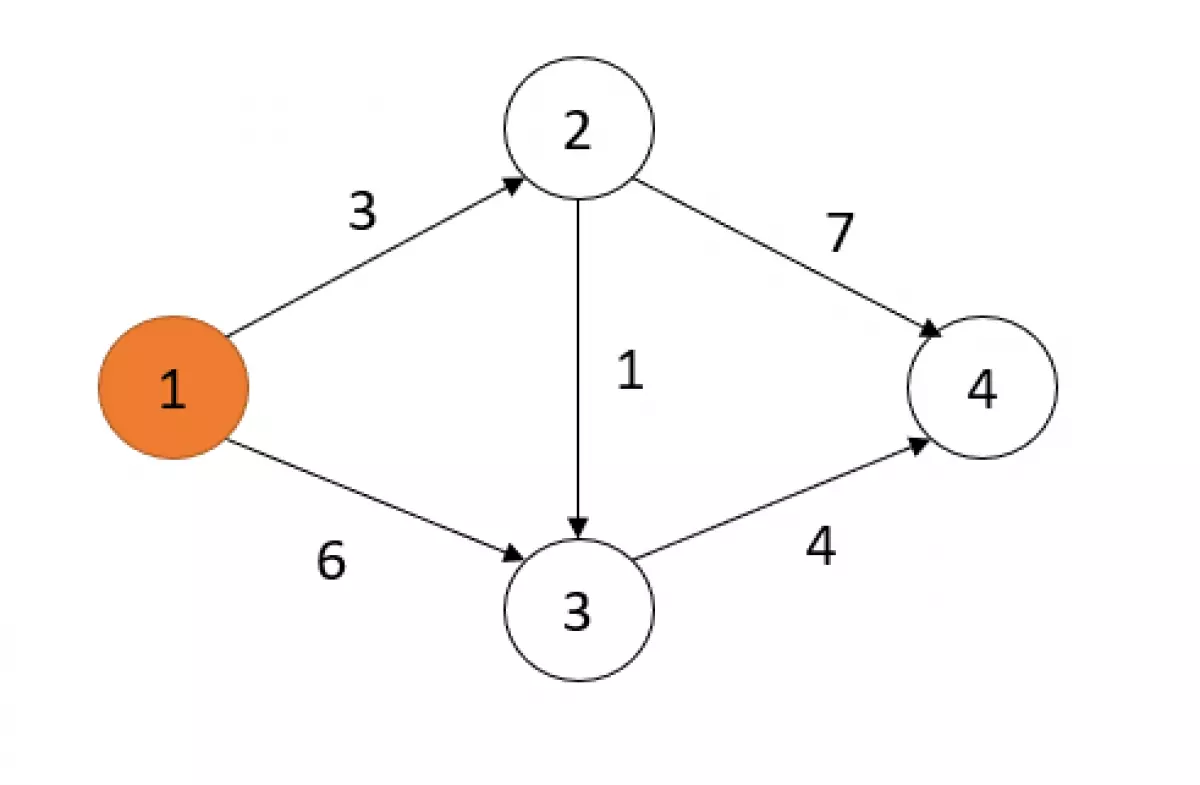
- Đầu tiên, dist = [0, ∞, ∞, ∞] và mark = [0, 0, 0, 0] (ta coi 0 là false và 1 là true).
- Ta chọn u = 1 do dist[1] = 0 nhỏ nhất và thoả mãn mark[1] = 0. Xét các đỉnh v có cạnh nối trực tiếp từ đỉnh 1.
- Xét v = 2, ta thấy dist[1] + độ dài cạnh (1, 2) = 3 < dist[2] = ∞ nên dist[2] = 3
- Xét v = 3, ta thấy dist[1] + độ dài cạnh (1, 3) = 6 < dist[3] = ∞ nên dist[3] = 6
- Do không còn đỉnh nối từ đỉnh 1 nên ta kết thúc xét đỉnh 1 và đánh dấu mark[1] = 1
- Khi này, dist = [0, 3, 6, ∞] và mark = [1, 0, 0, 0]
- Ta chọn u = 2 do dist[2] = 3 nhỏ nhất và thoả mãn mark[2] = 0. Xét các đỉnh v có cạnh nối trực tiếp từ đỉnh 2.
- Xét v = 3, ta thấy dist[2] + độ dài cạnh (2, 3) = 4 < dist[3] = 6 nên dist[3] = 4
- Xét v = 4, ta thấy dist[2] + độ dài cạnh (2, 4) = 10 < dist[4] = ∞ nên dist[4] = 10
- Do không còn đỉnh nối từ đỉnh 2 nên ta kết thúc xét đỉnh 2 và đánh dấu mark[2] = 1
- Khi này, dist = [0, 3, 4, 10] và mark = [1, 1, 0, 0]
- Ta chọn u = 3 do dist[3] = 4 nhỏ nhất và thoả mãn mark[3] = 0. Xét các đỉnh v có cạnh nối trực tiếp từ đỉnh 3.
- Xét v = 4, ta thấy dist[3] + độ dài cạnh (3, 4) = 8 < dist[4] = 10 nên dist[4] = 8
- Do không còn đỉnh nối từ đỉnh 3 nên ta kết thúc xét đỉnh 3 và đánh dấu mark[3] = 1
- Khi này, dist = [0, 3, 4, 8] và mark = [1, 1, 1, 0]
- Ta chọn u = 4 do dist[4] = 0 nhỏ nhất và thoả mãn mark[4] = 0. Xét các đỉnh v có cạnh nối trực tiếp từ đỉnh 4.
- Do không còn đỉnh nối từ đỉnh 4 nên ta kết thúc xét đỉnh 4 và đánh dấu mark[4] = 1
- Do tất cả các đỉnh đã được đánh dấu nên thuật toán kết thúc và ta thu được dist = [0, 3, 4, 8]
Code cơ bản
#include
using namespace std;
typedef long long ll;
const int MaxN = 1 + 1e2;
const ll INF = 1e18;
int n, m, s;
bool mark[MaxN];
ll dist[MaxN];
vector> adj[MaxN];
void Dijkstra(int s){
fill(dist + 1, dist + n + 1, INF);
dist[s] = 0;
for(int i = 1 ; i <= n ; ++i){
int v = -1;
for(int j = 1 ; j <= n ; ++j){
if(!mark[j] && (v == -1 || dist[j] < dist[v])) v = j;
}
if(v == -1) break;
mark[v] = 1;
for(auto u : adj[v]){
if(mark[u.first]) continue;
dist[u.first] = min(dist[u.first], dist[v] + u.second);
}
}
}
int main(){
cin >> n >> m >> s;
for(int i = 0 ; i < m ; ++i){
int u, v, w;
cin >> u >> v >> w;
adj[u].push_back({v, w});
}
Dijkstra(s);
for(int i = 1 ; i <= n ; ++i){
if(dist[i] == INF) cout << -1 << endl;
else cout << dist[i] << endl;
}
return 0;
} Độ phức tạp
Độ phức tạp của thuật toán Dijkstra là O(n^2 + m), trong đó n là số đỉnh của đồ thị và m là số cạnh. Vòng lặp ngoài cùng có độ phức tạp O(n). Vòng lặp trong cùng để tìm ra đỉnh u có dist[u] nhỏ nhất có độ phức tạp O(n). Vòng lặp để xét các đỉnh có cạnh nối trực tiếp từ u có độ phức tạp O(m). Tổng cộng, độ phức tạp là O(n^2 + m).
Code cải tiến
Thuật toán Dijkstra có thể được cải tiến bằng cách sử dụng priority_queue để tìm ra đỉnh u có dist[u] nhỏ nhất một cách nhanh chóng. Cải tiến này giúp giảm độ phức tạp của thuật toán xuống còn O(m log n).
#include
using namespace std;
typedef long long ll;
const int MaxN = 1 + 1e2;
const ll INF = 1e18;
int n, m, s;
bool mark[MaxN];
ll dist[MaxN];
vector> adj[MaxN];
void Dijkstra(int s){
fill(dist + 1, dist + n + 1, INF);
dist[s] = 0;
priority_queue, vector>, greater>> pq;
pq.push({0, s});
while(!pq.empty()){
int u = pq.top().second;
pq.pop();
if(mark[u]) continue;
mark[u] = true;
for(auto e : adj[u]){
int v = e.first;
ll w = e.second;
if(dist[v] > dist[u] + w){
dist[v] = dist[u] + w;
pq.push({dist[v], v});
}
}
}
}
int main(){
cin >> n >> m >> s;
for(int i = 0 ; i < m ; ++i){
int u, v, w;
cin >> u >> v >> w;
adj[u].push_back({v, w});
}
Dijkstra(s);
for(int i = 1 ; i <= n ; ++i){
if(dist[i] == INF) cout << -1 << endl;
else cout << dist[i] << endl;
}
return 0;
} Độ phức tạp
Khi sử dụng priority_queue, độ phức tạp của thuật toán Dijkstra giảm xuống còn O(m log n).
Vấn đề kì sau
Trong bài học kế tiếp, chúng ta sẽ tìm hiểu về thuật toán Bellman-Ford trong tìm kiếm đường đi ngắn nhất trên đồ thị. Trước đó, hãy để lại câu trả lời cho câu hỏi sau:
- Nếu các cạnh có trọng số âm, điều gì có thể xảy ra với thuật toán Dijkstra?
Kết luận
Qua bài học này, chúng ta đã nắm vững về thuật toán Dijkstra trong tìm kiếm đường đi ngắn nhất trên đồ thị. Bài học kế tiếp, chúng ta sẽ tìm hiểu về thuật toán Bellman-Ford. Nếu bạn có bất kỳ khó khăn hoặc thắc mắc nào, hãy để lại bình luận hoặc góp ý để chúng ta có thể phát triển bài viết tốt hơn. Cảm ơn bạn đã theo dõi!













