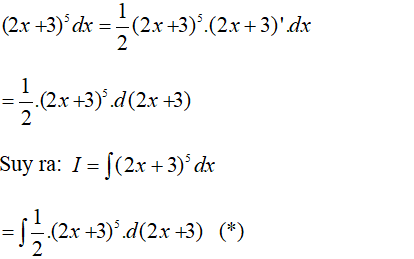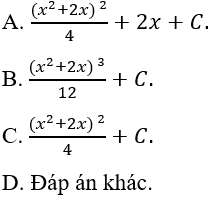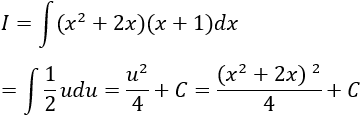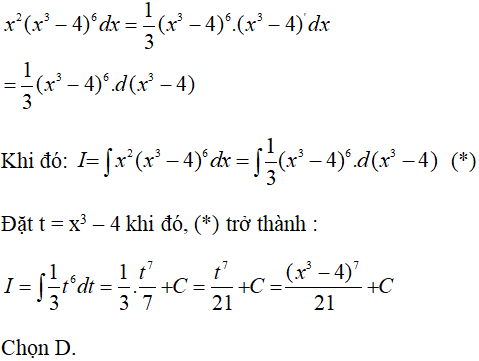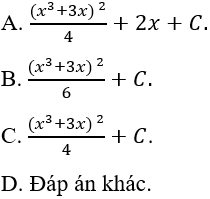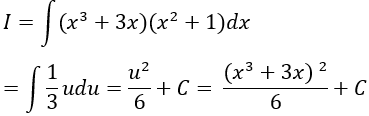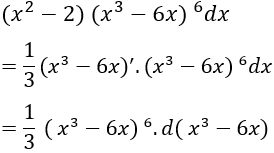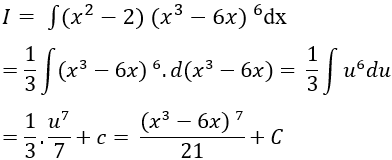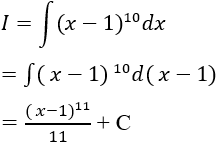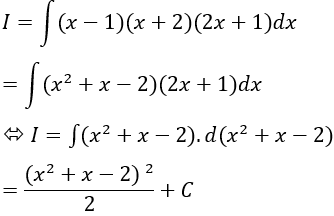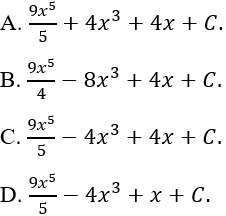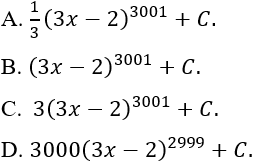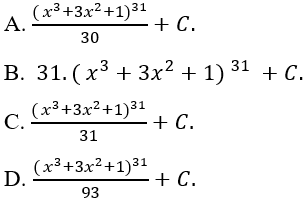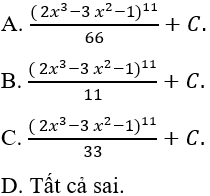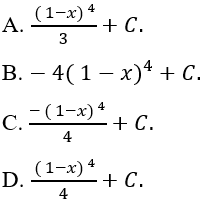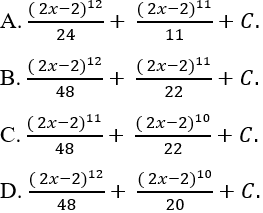Tìm nguyên hàm của hàm đa thức bằng phương pháp đổi biến số (cực hay)

Bài viết này giúp bạn ôn tập và nắm vững cách tìm nguyên hàm của hàm đa thức bằng phương pháp đổi biến số. Phương pháp này giúp chúng ta giải quyết các bài tập liên quan đến tích phân hàm một cách chi tiết và hiệu quả. Bài viết được dẫn chứng bằng ví dụ minh họa cụ thể và giải chi tiết từng bước.

Phương pháp giải

Đầu tiên, chúng ta đặt một biến số mới u = u(x), với u(x) là một hàm số có đạo hàm liên tục trên K và hàm số y = f(u) liên tục trên K. Nếu F là một nguyên hàm của f, thì ta có công thức sau:

∫f[u(x)]du = F(u(x)) + C

Trong đó, C là hằng số và xác định bởi định nghĩa nguyên hàm.

Ví dụ minh họa

Ví dụ 1: Tìm nguyên hàm của hàm số y = (2x + 3)^5

Giải:

Ta đặt u = 2x + 3, khi đó phương trình trở thành:

Chọn A.

Ví dụ 2: Tính I = ∫(x^2 + 2x)(x + 1)dx

Giải:

Ta có:

Đặt u = x^2 + 2x ta có:

Chọn C.

Ví dụ 3: Tính I = ∫x^2(x^3 - 4)^6dx

Giải:

Ta có:

Ví dụ 4: Tìm nguyên hàm của hàm số y = (2x - 3x^2)(x^2 - x^3 + 2)^5

Giải:

Ta có: (2x - 3x^2)(x^2 - x^3 + 2)^5.dx = (x^2 - x^3 + 2)^5(x^2 - x^3 + 2)'.dx = (x^2 - x^3 + 2)^5.d(x^2 - x^3 + 2)

⇒ I = ∫(2x - 3x^2)(x^2 - x^3 + 2)^5 dx = ∫(x^2 - x^3 + 2)^5 d(x^2 - x^3 + 2) (*)

Đặt u = x^2 - x^3 + 2; khi đó (*) trở thành:

Chọn A.

Ví dụ 5: Tính I = ∫(x^3 + 3x)(x^2 + 1)dx

Giải:

Ta có:

Đặt u = x^3 + 3x ta có:

Chọn B.

Ví dụ 6: Tính I = ∫(x^2 - 2)(x^3 - 6x)^6dx

Giải:

Ta có:

Đặt u = x^3 - 6x ta được:

Chọn B.

Ví dụ 7: Tính I = ∫(x - 1)^10dx

Giải:

Ta có:

Chọn C.

Ví dụ 8: Tính I = ∫(x - 1)(x + 2)(2x + 1)dx

Giải:

Ta có:

Chọn A.

Bài tập vận dụng

Câu 1: Tìm nguyên hàm của hàm số y = (3x^2 - 2)^2

Giải:

Ta có:

Chọn C.

Câu 2: Tìm nguyên hàm của hàm số y = (3x - 2)^{3000}

Giải:

Đặt t = 3x - 2 ⇒ dt = 3dx

Chọn A.

Câu 3: Tính nguyên hàm của hàm số y = (x^2 + 2x)(x^3 + 3x^2 + 1)^{30}

Giải:

Đặt t = x^3 + 3x^2 + 1 ⇒ dt = (3x^2 + 6x)dx

Chọn D.

Câu 4: Tính I = ∫x(x - 1)(2x^3 - 3x^2 - 1)^{10} dx

Giải:

Đặt t = 2x^3 - 3x^2 - 1

⇒ dt = 6x^2 - 6x = 6x(x - 1) dx

Chọn A.

Câu 5: Tính ∫(x - 1)(1 - x^2) dx

Giải:

Ta có:

Đặt t = 1 - x suy ra dt = -dx

Chọn C.

Câu 6: Tính I = ∫x(x - 1)^{209} dx

Giải:

Ta có: x(x - 1)^{209} = (x - 1)^{210} + (x - 1)^{209}

⇒ I = ∫x(x - 1)^{209} dx = ∫[(x - 1)^{210} + (x - 1)^{209}] dx

Đặt t = x - 1 ⇒ dt = dx

Chọn A.

Câu 7: Tính I = ∫x(2x - 2)^{10} dx

Giải:

Ta có:

Đặt t = 2x - 2 ⇒ dt = 2dx

Chọn B.

Bài giảng: Cách làm bài tập nguyên hàm và phương pháp tìm nguyên hàm của hàm số cực nhanh - Cô Nguyễn Phương Anh (Giáo viên VietJack)

Xem thêm các dạng bài tập Toán lớp 12 có trong đề thi THPT Quốc gia khác.