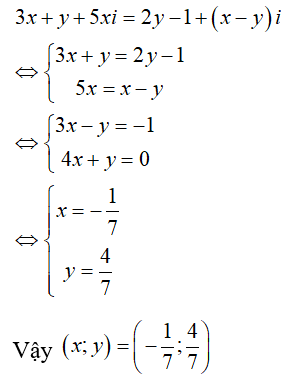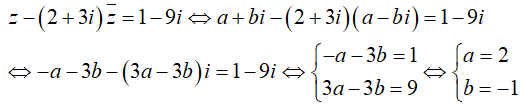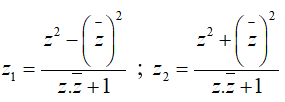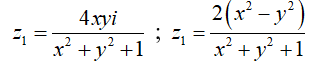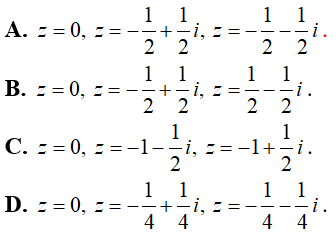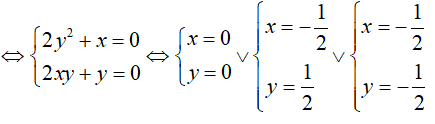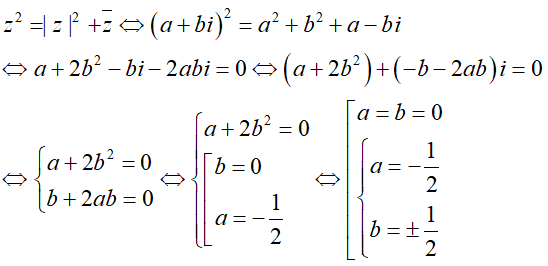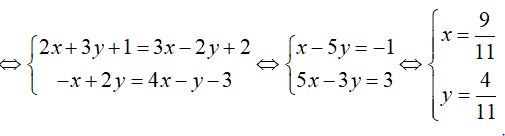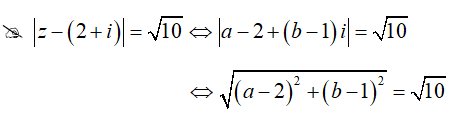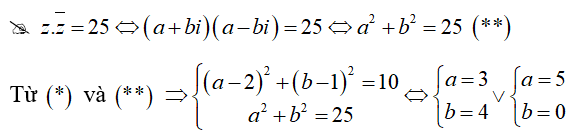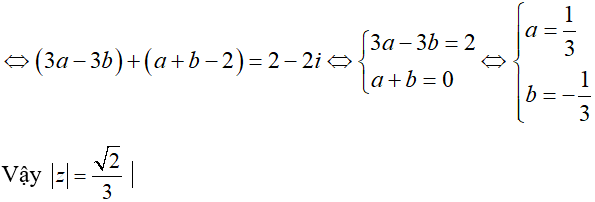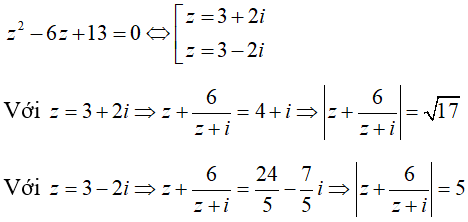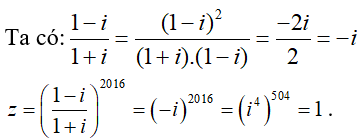Hãy cùng tìm hiểu về việc tìm số phức z thỏa mãn điều kiện cho trước cực hay trong bài toán Toán lớp 12. Chúng ta sẽ được làm quen với các phương pháp giải và các ví dụ minh họa cụ thể để hiểu rõ hơn về cách làm bài tập này.
A. Phương pháp giải & Ví dụ
Phương pháp giải
Trước tiên, hãy làm quen với phương pháp giải. Cho hai số phức z1 = a + bi và z2 = c + di, chúng ta có:
- Phép cộng số phức: z1 + z2 = (a + c) + (b + d)i
- Phép trừ số phức: z1 - z2 = (a - c) + (b - d)i
- Hai số phức z1 và z2 bằng nhau khi và chỉ khi a = c và b = d
Ví dụ minh họa
Hãy xem qua một số ví dụ minh họa để hiểu rõ hơn về cách áp dụng phương pháp giải.
Ví dụ 1: Các số thực x và y thỏa mãn: 3x + y + 5xi = 2y - 1 + (x - y)i là
Hướng dẫn:
Chọn đáp án A.
Ví dụ 2: Cho số phức z thỏa mãn: 3z + 2 = (4 - i)2. Môđun của số phức z là
A. -73. B. -√73. C. 73. D. √73.
Hướng dẫn:
Gọi z = a + bi => z̅ = a - bi
Hay 5a + bi = 15 - 8i
Vậy z = 3 - 8i
Chọn đáp án D.
Ví dụ 3: Tìm số phức z, biết z - (2 + 3i) = 1 - 9i.
A. z = -2 + i. B. z = -2 - i. C. z = 3 + 2i. D. z = 2 - i.
Hướng dẫn:
Gọi z = a + bi ta có:
Vậy z = 2 - i
Chọn đáp án D.
Ví dụ 4: Cho số phức z = a + bi thỏa mãn: z - (2 + 3i). Giá trị của ab + 1 là:
A. -1. B. 0. C. 1. D. -2.
Hướng dẫn:
Chọn đáp án A.
Ví dụ 5: Có bao nhiêu số phức z thỏa mãn |z| = √2 và z^2 là số thuần ảo?
A. 4. B. 3. C. 2. D. 1.
Hướng dẫn:
Gọi z = a + bi.
Ta có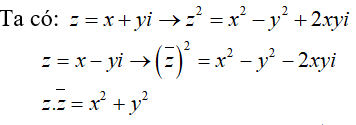 
và z^2 = a^2 - b^2 + 2abi
Yêu cầu của bài toán thỏa mãn khi và chỉ khi 
Vậy có 4 số phức thỏa mãn điều kiện bài toán
Chọn đáp án A.
Ví dụ 6: Cho 2 số phức với z = x + yi, x,y ∈ R.
Mệnh đề nào sau đây đúng?
A. z1 và z2 là số thuần ảo. B. z2 là số thuần ảo.
C. z1 là số thuần ảo. D. z1 và z2 là số thực.
Hướng dẫn:
Khi đó: 
Suy ra z1 là số thuần ảo; z2 là số thuần thực.
Chọn đáp án C.
Ví dụ 7: Tìm tất cả số phức z thỏa z2 = |z|^2 + 3.
Hướng dẫn:
Đặt z = x + yi
Ta có:
z^2 = |z|^2 + 3 <=> 2y^2 + x - (2xy + y)i = 0
Chọn đáp án A.
Ví dụ 8: Có bao nhiêu số phức thỏa mãn điều kiện z^2 = |z|^2 + ?
A. 3. B. 0. C. 1. D. 2.
Hướng dẫn:
Gọi z = a + bi là số phức thỏa mãn điều kiện trên.
Ta có:
Vậy có 3 số phức thỏa mãn yêu cầu bài toán.
Chọn đáp án A.
B. Bài tập vận dụng
Câu 1: Các số thực x và y thỏa mãn: (2x + 3y + 1) + (-x + 2y)i = (3x - 2y + 2) + (4x - y - 3)i là
Lời giải:
Đáp án: B
Giải thích:
(2x + 3y + 1) + (-x + 2y)i = (3x - 2y + 2) + (4x - y - 3)i
Câu 2: Số phức z thỏa mãn: z - (2 + 3i) = 1 - 9i là
A. z = -2 + i. B. z = -2 - i. C. z = 3 + 2i. D. z = 2 - i.
Lời giải:
Đáp án: D
Giải thích:
Gọi z = a + bi với a,b ∈ R ; i^2 = -1 => z = a - bi
z - (2 + 3i) = 1 - 9i
<=> a + bi - (2a - 2bi + 3ai + 3b) = 1 - 9i
<=> -a - 3b + (-3 + 3b)i = 1 - 9i
Câu 3: Tìm số phức z thỏa mãn hệ thức 
A. z = 3 + 4i; z = 5. B. z = 3 + 4i; z = -4.
C. z = -3 + 4i; z = 5. D. z = 3 - 4i; z = -5.
Lời giải:
Đáp án: A
Giải thích:
Gọi z = a + bi khi đó 
Hay (a-2)^2 + (b-1)^2 = 10 (*)
Vậy z = 3 + 4i hoặc z = 5.
Câu 4: Tìm số thực x, y để hai số phức z1 = 9y^2 - 4 - 10xi^5 và z2 = 82 + 20i^11 là liên hợp của nhau?
A. x = -2; y = 2. B. x = 2; y = ±2.
C. x = 2; y = 2. D. x = -2 ; y = ±2.
Lời giải:
Đáp án: D
Giải thích:
z1 và z2 là liên hợp của nhau khi và chỉ khi:
Câu 5: Cho số phức z thỏa mãn (2z - 1)(1 + i) + (i + 1)(1 - i) = 2 - 2i. Giá trị của |z| là ?
A. √17 hoặc 5. B. -√17 hoặc √175.
C. √17 hoặc 4. D. √17 hoặc √5.
Lời giải:
Đáp án: A
Giải thích:
Gọi z = a + bi ta có :
(2z - 1)(1 + i) + (i + 1)(1 - i) = 2 - 2i
<=> [(2a - 1) + 2bi](1 + i) + [(a + 1) - bi](1 - i) = 2 - 2i
<=> (2a - 2b - 1) + (2a + 2b - 1) = (a - b + 1) - (a + b + 1)i = 2 - 2i
Câu 6: Cho số phức z thỏa mãn z^2 - 6z + 13 = 0. Giá trị của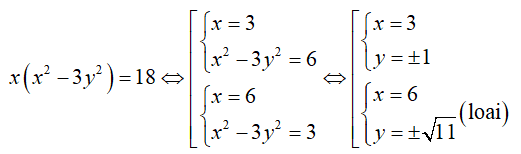 
là:
A. √17 hoặc 5. B. -√17 hoặc √175.
C. √17 hoặc 4. D. √17 hoặc √5.
Lời giải:
Đáp án: A
Giải thích:
Câu 7: Cho số phức z thỏa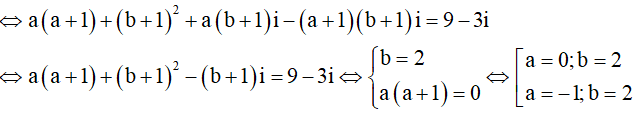 
. Viết z dưới dạng z = a + bi. Khi đó tổng a+b có giá trị bằng bao nhiêu?
A. 3. B. -1. C. 1. D. 2.
Lời giải:
Đáp án: C
Giải thích:
Gọi z = a + bi là số phức thỏa mãn đẳng thức trên. Ta có:
Do |z| > 2 => a = -1; b = 2 => a + b = 1
Như vậy, tổng a+b có giá trị là 1.
