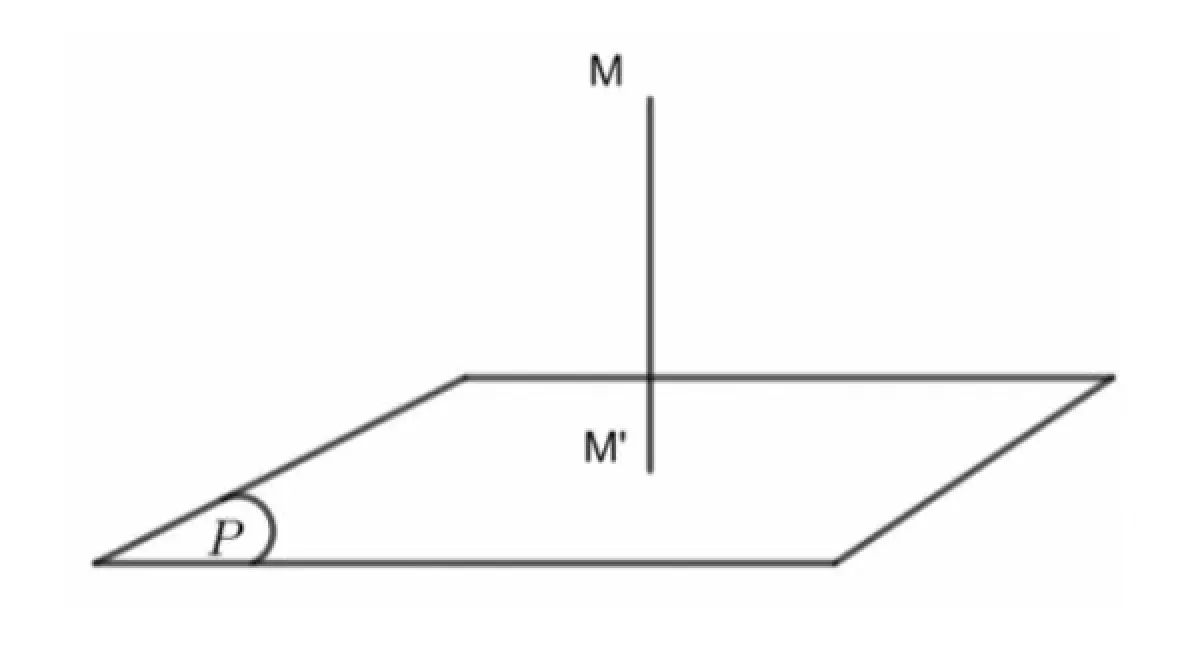
Định nghĩa khoảng cách từ điểm đến mặt phẳng
Cho một điểm M và một mặt phẳng (P) bất kì. Ta có khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa 2 điểm M và H với H là hình chiếu của M đến mặt phẳng (P).
Ký hiệu: d(M, (P)) = MH
Công thức tính khoảng cách điểm đến mặt phẳng trong không gian tọa độ
Trong hệ tọa độ không gian Oxyz, cho điểm M có tọa độ như sau: (α; β; γ). Cho mặt phẳng (P) có phương trình dạng ax + by + cz + d = 0. Công thức tổng quát tính khoảng cách từ điểm M đến mặt phẳng (P) được tính như sau:
d(M, (P)) = |aα + bβ + cγ + d|/√(a^2 + b^2 + c^2)
Các phương pháp tính khoảng cách từ điểm đến mặt phẳng
Phương pháp số 1: Dựa vào định nghĩa
Theo đúng như định nghĩa, để tính được khoảng cách từ điểm M tới mặt phẳng (P) chúng ta sẽ tìm hình chiếu của M trên mặt phẳng (ta gọi là điểm H) rồi tính độ dài MH dựa trên công thức tính khoảng cách.
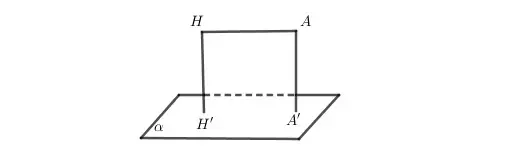
Phương pháp số 2: Tính khoảng cách gián tiếp
Ta tìm một điểm H’ sao cho đường thẳng đi qua M và H’ song song với mặt phẳng P. Vậy từ đó ta có thể suy ra được khoảng cách từ M đến mặt phẳng P bằng khoảng cách từ H’ đến P.
d(M, (P)) = d(H’, (P))
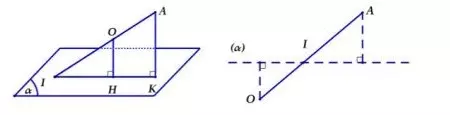
Phương pháp số 3: Sử dụng tam giác đồng dạng
Tìm 1 điểm O xác định, ta tìm giao điểm của OA với mặt phẳng (P) là I. Vậy ta tính khoảng cách từ d(O,(α))/d(A,(α)) = OI/AI (dựa theo định lý Ta-lét)

Với 3 phương pháp đã liệt kê ở trên, các em học sinh hoàn toàn có thể dễ dàng tính được khoảng cách từ điểm bất kì nào đó tới một mặt phẳng cho trước. Về cơ bản, đối với các bài tập của dạng này, các em sẽ phải đưa bài toán về dạng tìm khoảng cách từ điểm đó với hình chiếu của nó trên mặt phẳng hoặc sử dụng định lý Ta-lét, tam giác đồng dạng để tính khoảng cách.
Đăng ký ngay để được các thầy cô tư vấn và xây dựng lộ trình ôn thi THPT sớm đạt 27+.
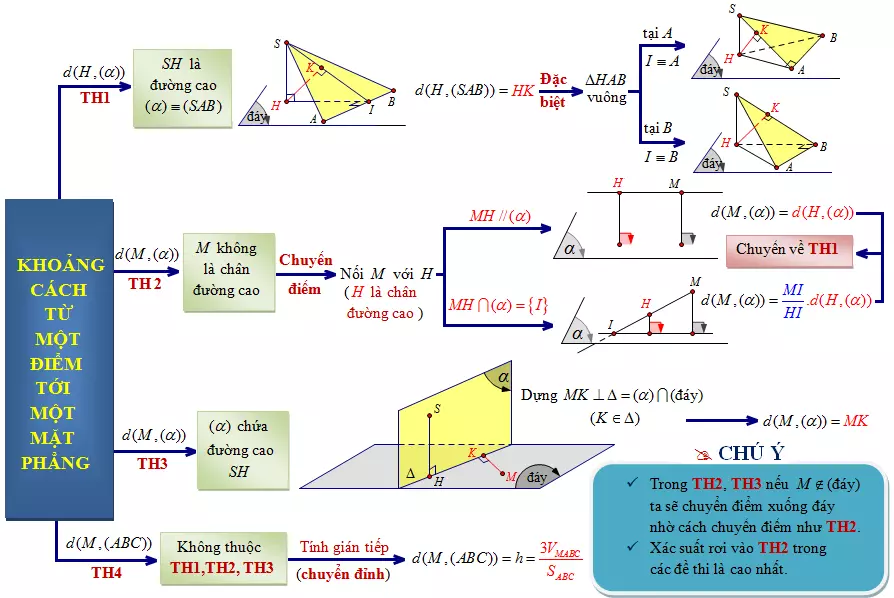
Sơ đồ tư duy khoảng cách từ điểm tới mặt phẳng
Bài tập luyện tập tính khoảng cách từ một điểm tới một mặt phẳng
Bài tập 1
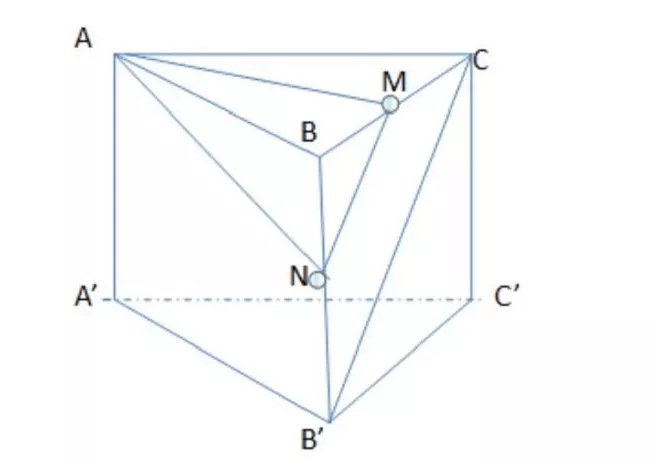
Cho lăng trụ đứng ABC.A’B’C’ với đáy là một tam giác vuông cân ABC với BC = BA = a, độ dài cạnh bên AA’ có kích thước là a√2. Gọi trung điểm của đoạn thẳng BC là M, hãy tính khoảng cách giữa 2 đường thẳng AM với B’C’.
Hướng dẫn giải
Gọi trung điểm của cạnh bên BB’ là N. Lúc này đoạn thẳng MN là đường trung bình của tam giác BB’C. Suy ra: B’C song song MN => B'C song song với mặt phẳng (AMN) Vậy ta có khoảng cách từ B'C đến mặt đến AM là d(B’C; AM) = d(B’C; (AMN)) = d(B’; (AMN))
Mà BB' giao với mặt phẳng (AMN) tại điểm N, mà N là trung điểm của BB’. Suy ra: d(B’; (AMN)) = d(B; (AMN))
Ta có: Hình chóp A.BMN có BA, BM và BN có một góc vuông
=>
Vậy khoảng cách từ điểm B' đến mặt phẳng (AM) là
Bài tập 2
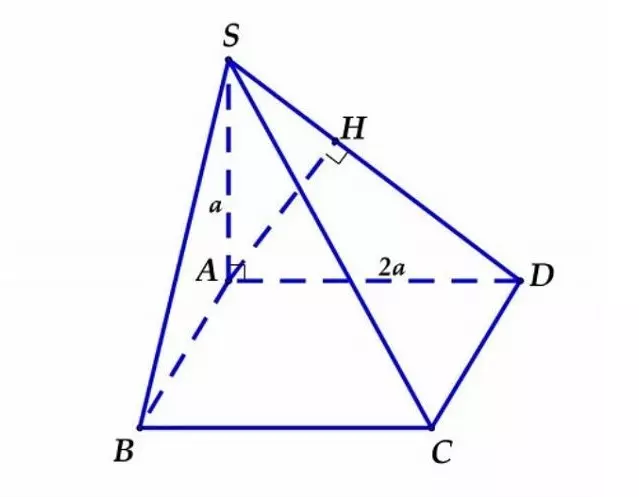
Cho hình chóp S.ABCD có đáy là hình chữ nhất ABCD, biết độ dài cạnh AD = 2a và vuông góc với đáy, cạnh SA có độ dài là a. Hãy tính khoảng cách từ điểm A tới mặt phẳng (SCD)?
Hướng dẫn giải
Trong mặt phẳng (SAD) ta kẻ đường thẳng AH vuông góc với đoạn thẳng SD (với điểm H nằm trên đoạn thẳng SD)
Vì CD vuông góc AD và CD vuông góc SA. Suy ra: SA vuông góc với mặt phẳng (SAD)
=> CD ⊥ AH
Vì AH vuông góc SD và AH vuông góc CD Suy ra: AH vuông góc với mặt phẳng (SCD)
Bài tập 3
Cho hình chóp S.ABC có đáy là tam giác vuông ABC tại B. Biết rằng độ dài các cạnh BA là a, BC là 2a và cạnh SA có độ dài là 2a, đồng thời cạnh SA vuông góc với mặt phẳng (ABC). Gọi điểm K là hình chiếu của A lên đường thẳng SC. Tính khoảng cách từ điểm K đến mặt phẳng (SAB)?
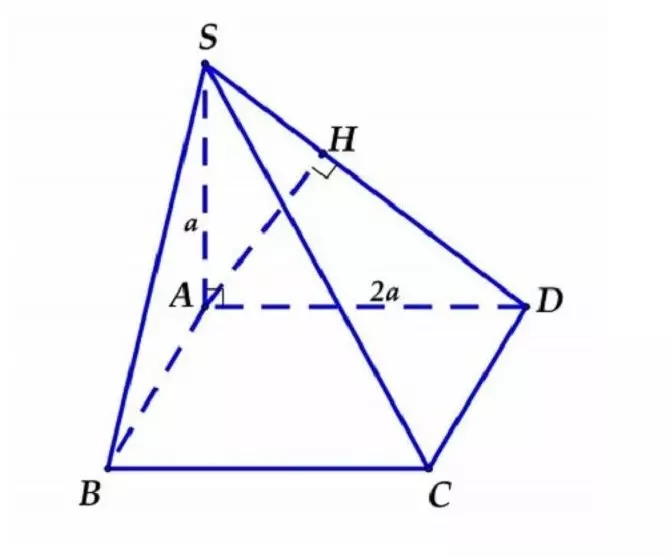
Hướng dẫn giải
Ta có: SA vuông góc với mặt phẳng (ABC) => SA ⊥ BC (1) Ta có tam giác ABC có góc vuông tại B => BC ⊥ AB (2) Từ (1) và (2) => BC song song với mặt phẳng (SAB) Trong mặt phẳng (SBC), ta kẻ một đường thẳng KH song song với cạnh BC (với điểm H nằm trên cạnh SB) => KH vuông góc với mặt phẳng (SAB) Suy ra: ta có khoảng cách từ điểm K tới mặt phẳng (SAB) là: d(K; (SAB)) = KH
Ta có SI = a√3/2 và ID = a√5/2
Vậy khoảng cách từ điểm K đến mặt phẳng (SAB) là
Bài tập 4
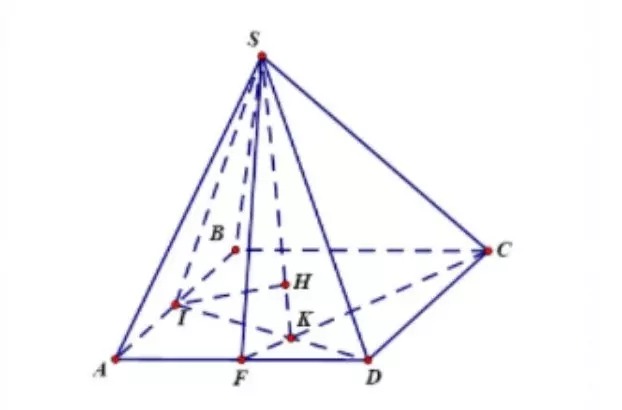
Cho một hình chóp S.ABCD, có đáy là hình vuông ABCD có cạnh là a. Biết rằng tam giác SAB là một tam giác đều và mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Gọi 2 điểm I và F lần lượt là trung điểm của AB và AD, hãy tính khoảng cách từ điểm I tới mặt phẳng SFC?

Hướng dẫn giải
Gọi điểm K là điểm giao nhau của 2 đoạn thẳng ID và FC
Kẻ đoạn thẳng IH vuông góc với SK (với điểm H nằm trên đoạn thẳng SK)
Ta có: mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD) và mặt phẳng (SAB) giao với mặt phẳng (ABCD) là đoạn thẳng AB và SI ⊂ (SAB)
Suy ra:
SI ⊥ (ABCD) => SI ⊥ FC (1)
Bên cạnh đó, ta xét 2 tam giác vuông AID và DFC có:
AI = DF và AD = DC
=> Δ AID = Δ DFC
=> ta có:
và
Mà
=> FC vuông góc với ID (2)
Từ (1) và (2) ta có: FC vuông góc với mặt phẳng (SID)
=> IH ⊥ FC (*)
Từ () và (**) => IH vuông góc với mặt phẳng (SFC)
Vậy khoảng cách từ điểm I đến mặt phẳng (SFC) là d(I, (SFC)) = IH
Ta có SI = a√3/2 và ID = a√5/2
Vậy khoảng cách từ điểm I đến mặt phẳng (SFC) là d(I, (SFC)) = IH =
Bài tập 5
Cho một hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, biết rằng độ dài cạnh AD = AB = a và độ dài cạnh CD = 2a, SD = a. T có SD vuông góc với mặt phẳng (ABCD).
a, Tính
b, Tính
Hướng dẫn giải
Gọi trung điểm của cạnh CD là điểm M Gọi giao diện của 2 đường thẳng BC và AD là điểm E
a, Kẻ đoạn thẳng DH vuông góc với SB thuộc mặt phẳng (SBD) với điểm H nằm trên cạnh SB (*)
Do BM = AD = 1/2 CD => Tam giác ∆ BCD vuông tại B => BC vuông góc BD (1)
Mặt khác, vì SD vuông góc với mặt phẳng (ABCD) => SD ⊥ BC (2)
Từ (1) và (2) => DH vuông góc với mặt phẳng (SBC)
=>
Xét tam giác SBD vuông tại đỉnh D
=>
=> DH =
Vậy khoảng cách từ điểm D đến mặt phẳng SBC là d(D, (SBC)) = DH =
b, Ta có:
=> d(A, (SBC)) =
d(D%2C%20%28SBC%29)) =
Trên đây là toàn bộ kiến thức cũng như các phương pháp tính khoảng cách từ điểm đến mặt phẳng trong chương trình toán 11. Để tìm hiểu thêm về kiến thức của các môn học khác, các em học sinh có thể truy cập VUIHOC. Chúc các em đạt kết quả tốt trong các kỳ thi trong tương lai.
Bài viết tham khảo thêm:












