Đạo hàm là một trong những phần kiến thức Toán quan trọng của học sinh cấp 3. Nắm vững kiến thức này không chỉ giúp các em đạt điểm cao trong các cuộc thi tốt nghiệp, thi đại học mà còn cần thiết trong quá trình học đại học sau này. Để giúp các bạn ôn lại nội dung này một cách đơn giản và dễ hiểu, hãy cùng trường mầm non Sakura Montessori tham khảo tổng hợp các công thức mới nhất trong bài viết dưới đây.
Tổng hợp các công thức đạo hàm mới nhất lớp 11, 12 [Bản đầy đủ 2023]
Định nghĩa & quy tắc cơ bản
Đạo hàm là một kiến thức quan trọng trong bài thi tốt nghiệp THPT quốc gia, do đó tất cả học sinh đều cần phải nắm vững phần này. Tuy nhiên, nhiều người học cảm thấy khó khăn với phần này. Để học tốt, chúng ta cần hiểu về định nghĩa và quy tắc cơ bản của đạo hàm.
1. Định nghĩa
Đạo hàm là một hàm số, dùng để mô tả sự biến thiên tại một điểm của hàm số. Nó chính là tỉ số giữa số gia và hàm số tại một điểm x0. Trong đó, chiều biến thiên và độ lớn của biến thiên thể hiện giá trị của đạo hàm.
Định nghĩa đạo hàm
2. Quy tắc cơ bản để áp dụng công thức đạo hàm lớp 11
Để áp dụng công thức đạo hàm lớp 11 một cách chính xác và nhanh chóng, chúng ta cần nắm vững các quy tắc cơ bản sau:
Quy tắc cơ bản để áp dụng công thức đạo hàm lớp 11
Công thức Đạo hàm tổng quan
Công thức đạo hàm tổng quan bao gồm 3 dạng:
- Đạo hàm của f(u) với u là hàm số
- (f(x))’ với x là biến số
- Đạo hàm của một số phân thức hữu tỉ
Công thức đạo hàm tổng quan
Công thức Đạo hàm sơ cấp
Công thức đạo hàm sơ cấp:
Ảnh công thức Đạo hàm sơ cấp (sưu tầm Internet)
Công thức Đạo hàm cấp cao
Công thức Đạo hàm cấp cao:
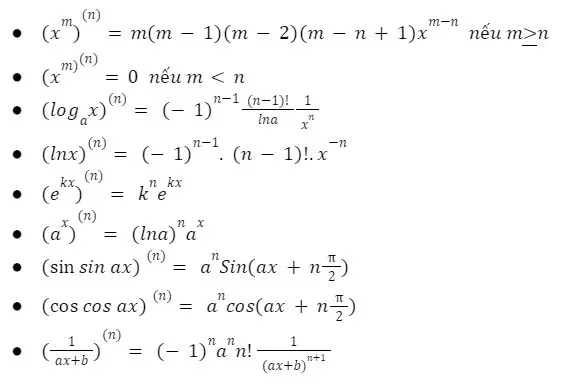Ảnh công thức Đạo hàm cấp cao (sưu tầm Internet)
Công thức Đạo hàm lượng giác
Công thức Đạo hàm lượng giác và hàm lượng giác ngược:
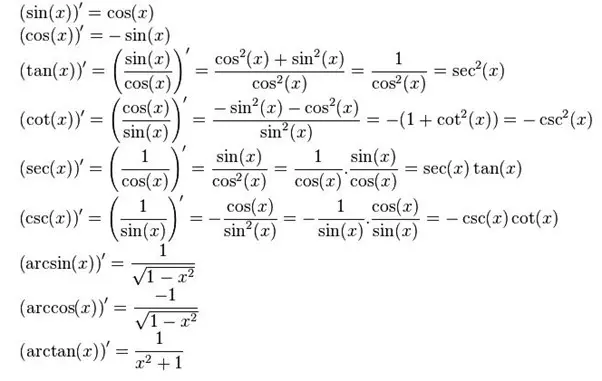Ảnh công thức Đạo hàm lượng giác (sưu tầm Internet)
Bảng công thức Đạo hàm mới nhất 2023
Bảng công thức mới nhất 2023:
Bảng công thức Đạo hàm (sưu tầm Internet)
Các dạng bài tập liên quan
Để hiểu rõ hơn về cách áp dụng công thức đạo hàm và giải các bài tập, chúng ta cần luyện tập với nhiều dạng bài tập khác nhau. Dưới đây là một số dạng bài tập phổ biến:
Dạng 1: Dạng bài tập đạo hàm áp dụng khái niệm, định nghĩa đạo hàm
Dạng bài tập này yêu cầu áp dụng khái niệm và định nghĩa để giải các bài toán cơ bản và đơn giản.
Dạng 2: Viết phương trình tiếp tuyến của hàm số
Đây là dạng bài tập phổ biến, yêu cầu viết phương trình tiếp tuyến của hàm số và tìm điểm tiếp điểm.
Dạng 3: Chứng minh đẳng thức dựa vào điều kiện liên quan đến đạo hàm
Dạng bài tập này yêu cầu chứng minh các đẳng thức dựa vào các điều kiện có sẵn liên quan đến đạo hàm.
Dạng 4: Phương trình và bất phương trình
Dạng bài tập này yêu cầu kết hợp các công thức đạo hàm và nguyên hàm để giải phương trình và bất phương trình đã cho.
Dạng 5: Cho hệ số góc, viết phương trình tiếp
Dạng bài tập này yêu cầu viết phương trình tiếp tuyến có hệ số góc đã cho.
Dạng 6: Áp dụng công thức đạo hàm, nguyên hàm giải bài tập
Dạng bài tập này yêu cầu áp dụng công thức đạo hàm và nguyên hàm để giải các bài tập phức tạp.
Dạng 7: Tính đạo hàm cấp cao
Dạng bài tập này yêu cầu tính đạo hàm cấp cao, từ cấp 2 trở lên.
Một số câu hỏi thường gặp
1. Cách ghi nhớ bảng đạo hàm hiệu quả?
Để ghi nhớ bảng đạo hàm hiệu quả, các em có thể áp dụng các cách sau:
- Học tập nghiêm túc
- Tích cực trao đổi thông tin với bạn bè và giáo viên
- Tích cực luyện các dạng bài tập
- Tìm tòi, nghiên cứu mở rộng kiến thức
2. Cách giải bài tập đạo hàm nhanh nhất?
Để giải bài tập đạo hàm nhanh chóng, các em cần:
- Nắm vững kiến thức lý thuyết về đạo hàm
- Vận dụng kiến thức vào giải các dạng bài tập
- Thực hành làm đa dạng các bài tập
- Tìm tòi, nghiên cứu mở rộng kiến thức
3. Công cụ tính đạo hàm online?
Có nhiều website miễn phí và chính xác để tính đạo hàm online, như:
- banhoituidap.com
- mathpapa.com
- wolfamalpha.com
- Mathway
- symbolab.com
Đạo hàm là một phần kiến thức quan trọng trong Toán học. Học sinh cần nắm vững công thức và luyện tập đa dạng các bài tập để hiểu sâu và áp dụng thành thạo. Nếu cần hỗ trợ, hãy liên hệ với thầy cô giáo hoặc liên hệ với chúng tôi. Chúc các em học tốt và đạt kết quả cao trong các kỳ thi sắp tới.
