Tứ giác là một loại hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó, không có hai đoạn thẳng nào cùng nằm trên một đường thẳng. Trong tứ giác ABCD, có những đặc điểm sau:
- Hai cạnh kề nhau không cùng thuộc một đường thẳng.
- Không có ba đỉnh nào thẳng hàng với nhau.
- Tên góc có thể được đọc theo tên đỉnh.
- Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.
- Quy ước: Khi nói về tứ giác mà không chú thích thêm thì ta hiểu đó là tứ giác lồi.
Tổng các góc của một tứ giác
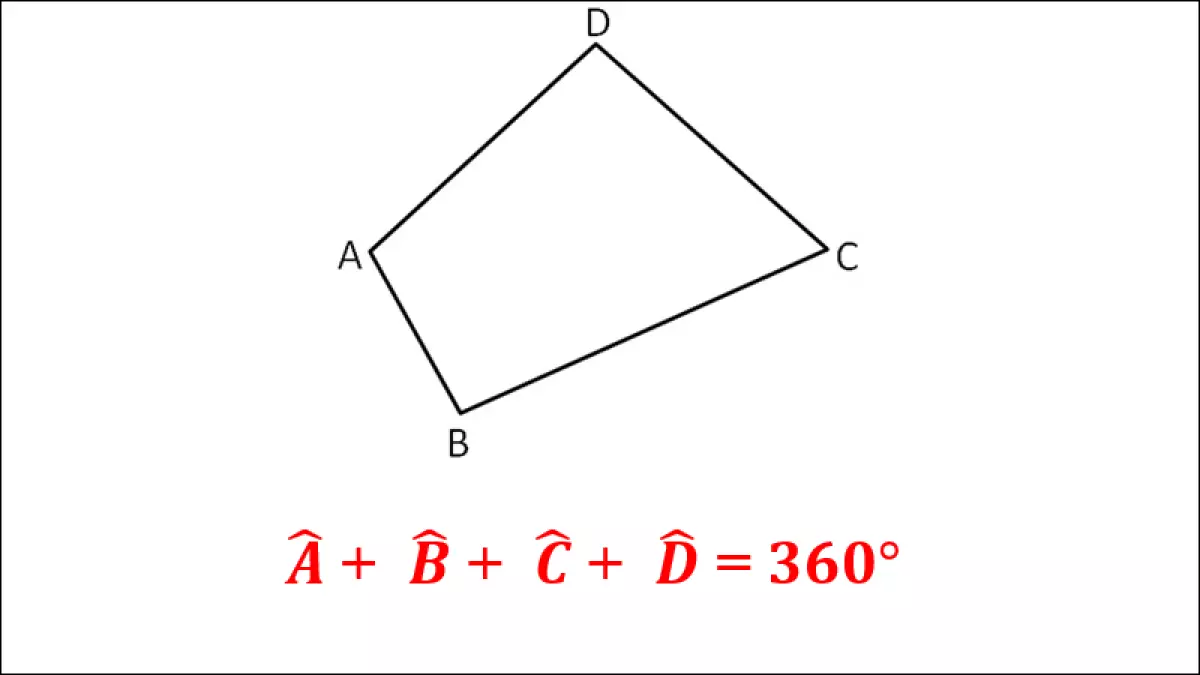
Tổng các góc của một tứ giác luôn bằng 360 độ. Ví dụ, trong tứ giác ABCD, tổng các góc là 360 độ.
Bài tập về tứ giác lớp 8 chương trình mới
Bài tập về tứ giác sách chân trời sáng tạo
Bài 1 trang 66 SGK toán 8/1 chân trời sáng tạo
a. Xét tứ giác ABCD có:
b. Xét tứ giác MNPQ có:
c. Đường thẳng TSV kề bù với góc có số đo bằng 60 độ. Vậy góc TSV bằng 180 độ - 120 độ. Xét tứ giác STUV có:
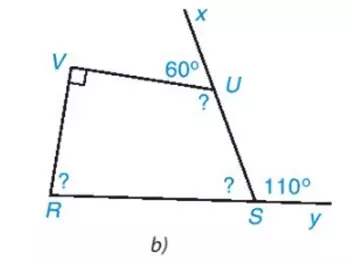
d. Xét tứ giác EFGH có:
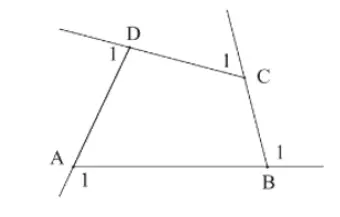
Bài 2 trang 66 SGK toán 8/1 chân trời sáng tạo
Xét tứ giác ABCD có:

Mặt khác:
Vậy:
Vậy tổng số đo của bốn góc ngoài tứ giác ABCD = 360 độ.
Bài 3 trang 67 SGK toán 8/1 chân trời sáng tạo

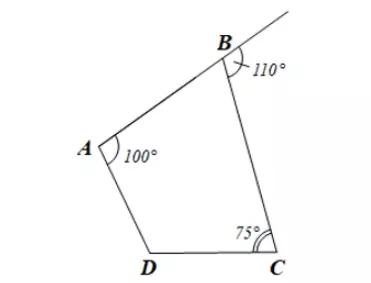
Do góc ngoài tại đỉnh B có số đo bằng 110 độ, nên góc ABC = 180 độ - 110 độ = 70 độ.
Xét tứ giác ABCD có:

Vậy:
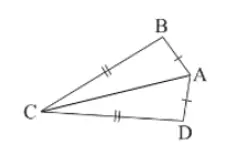
Bài 4 trang 67 SGK toán 8/1 chân trời sáng tạo
Gọi lần lượt là các góc ngoài tại đỉnh A, B, C, D.
Áp dụng kết quả của Bài tập 2, trang 66 Sách giáo khoa Toán 8, Tập một cho tứ giác ABCD ta có:
Vậy góc ngoài tại đỉnh D có số đo bằng 135°.
Bài 5 trang 67 SGK toán 8/1 chân trời sáng tạo
Xét tứ giác ABCD có:

=> x + 2x + 3x + 4x = 360°. Hay 10x = 360° => x = 36°.
Vậy:
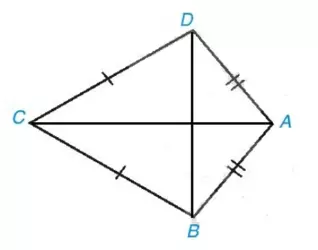
Bài 6 trang 67 SGK toán 8/1 chân trời sáng tạo
a) Vì AB = AD nên A nằm trên đường trung trực của đoạn thẳng BD. Vì CB = CD nên C nằm trên đường trung trực của đoạn thẳng BD. Do đó AC là đường trung trực của đoạn thẳng BD.
b) Xét DABC và DADC có:
- AC là cạnh chung.
- AB = AD; BC = DC (giả thiết).
Do đó DABC = DADC.
Vậy (hai góc tương ứng).
Vậy
Bài 7 trang 67 SGK toán 8/1 chân trời sáng tạo

a) Tứ giác BDNQ có:
- Các cạnh kề: BD và BQ; DB và DN; ND và NQ; QN và QB.
- Các cạnh đối: BD và NQ; DN và BQ.
b) Tứ giác BDNQ có các đường chéo BN và DQ.
Kết luận
Bài tập về tứ giác lớp 8 chương trình mới cung cấp những ví dụ và thực hành để học sinh nắm vững kiến thức về tứ giác. Việc hiểu và áp dụng các định lí và quy tắc về tứ giác sẽ giúp học sinh phát triển tư duy logic và khả năng vận dụng trong giải quyết các bài toán toán học.













