30 Bài tập Tìm đạo hàm cấp cao của hàm số cực hay (2024) có đáp án

Bạn đã từng gặp khó khăn trong việc tìm đạo hàm cấp cao của một hàm số? Bài viết này sẽ giúp bạn hiểu rõ hơn về cách tìm đạo hàm cấp cao cũng như các phương pháp giải cụ thể. Cùng tìm hiểu nhé!

Phương pháp giải

Đạo hàm cấp hai: Cho hàm số f(x) có đạo hàm f '(x). Nếu f '(x) cũng có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp hai của f(x) và được kí hiệu là: f ''(x), tức là:

f ’’(x) = (f’(x))’

Đạo hàm cấp n: Cho hàm số f(x) có đạo hàm cấp n - 1 (với n ∈ N, n ≥ 2)) là f(n-1)(x). Nếu f(n-1)(x) cũng có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của f(x) và được kí hiệu là f(n)(x), tức là:

f(n)(x) = (f(n-1)(x))'

Để tính đạo hàm cấp n:

• Tính đạo hàm cấp 1, 2, 3, ..., từ đó dự đoán công thức đạo hàm cấp n
• Dùng phương pháp quy nạp toán học để chứng minh công thức đúng

Ví dụ minh họa

Ví dụ 1: Hàm số .Tính đạo hàm cấp 2 của hàm số trên.

Hướng dẫn:

Ta có:

Ví dụ 2: Hàm số y = (x) = cos⁡(2x - π/3) . Phương trình f(4)(x) = -8 có nghiệm x ∈ [0; π/2] là:

Hướng dẫn:

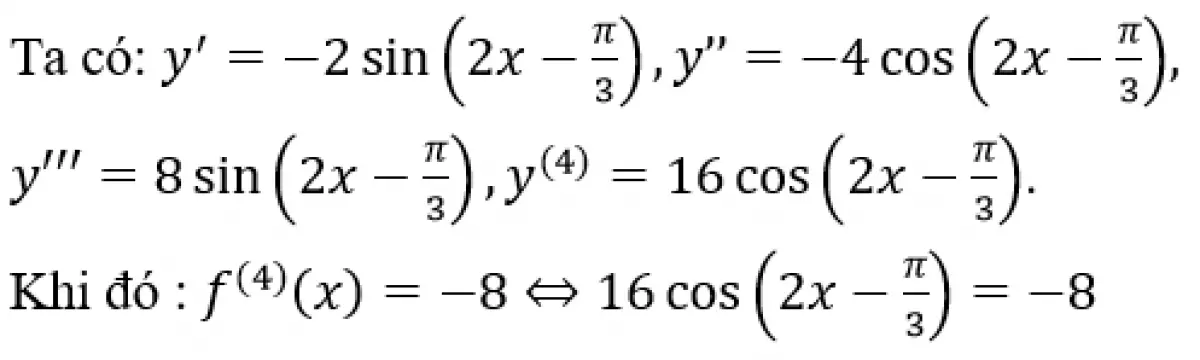
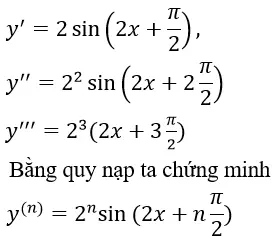
Ví dụ 3: Cho hàm số f(x) = 5(x+1)3 + 4(x+1)

Tìm tập nghiệm của phương trình f ''(x) = 0 ?

Hướng dẫn:

Vì: f '(x) = 15(x+1)2 + 4 ; f ''(x) = 30(x+1) ⇒ f ''(x) = 0 ⇔ x = -1

Ví dụ 4: Cho hàm số y = sin2⁡2x. Tính y(4)(π/6) ?

Hướng dẫn:

Vì: y ' = 2sin2x(2cos2x) = 2sin4x; y '' = 8cos4x; y ''' = -32sin4x;

y(4) = -128cos4x ⇒ y(4)(π/6) = 64√3

Ví dụ 5: Cho hàm số y = sin2x. Tính y’’

Hướng dẫn:

Ta có y' = 2cos2x ⇒ y '' = -4sin2x

Ví dụ 6: Cho hàm số y = sin2x. Tính y ''(π/3), y(4)(π/4) ?

Hướng dẫn:

Ta có y ''' = -8cos2x, y(4) = 16sin2x

Suy ra y ''' (π/3)= -8cos(2π/3) = 4; y(4)(π/4) = 16

Ví dụ 7: Cho hàm số y = sin2x. Tính y(n)?

Hướng dẫn:

Ta có

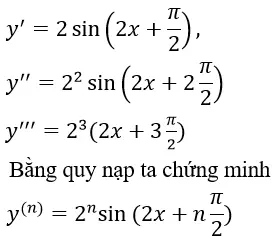
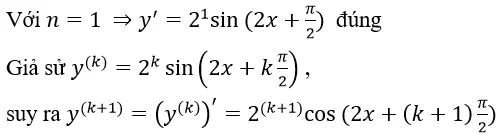
Theo nguyên lí quy nạp ta có điều phải chứng minh.

Bài tập vận dụng (có đáp án)

Bài 1: Đạo hàm cấp hai của hàm số y = (3/4)x4 - 2x3 - 5x + sinx bằng biểu thức nào sau đây?

A. 9x2-12x+sinx
B. 9x2-12x-sinx
C. 9x2-6x-sinx
D. 9x2-12x+cosx

Lời giải:

Đáp án: B

y’ = 3x3 - 6x2 - 5 + cosx. Do đó y” = 9x2 - 12x - sinx. Chọn đáp án B

Bài 2: Đạo hàm cấp 4 của hàm số y = sin2x bằng biểu thức nào sau đây?

Lời giải:

Đáp án: D

y’ = 2sinxcosx = sin2x

Chọn đáp án D

Bài 3: Đạo hàm cấp hai của hàm số y = 1/(2x-3) bằng biểu thức nào dưới đây?

Lời giải:

Đáp án: A

Ta có:

y’ = -(1/2)(2/(2x-3)^2)

y’’ = (1/2)(4/(2x-3)^3) = 2/(2x-3)^3

Đáp án A

Bài 4: Đạo hàm cấp hai của hàm số y = cosx.cos2x.cos3x bằng biểu thức nào dưới đây?

A. cos2x + 4cos4x + 9cos6x
B. - cos2x - 4cos4x - 9cos6x
C. - cosx - 4cos2x - 9cos3x
D. (-1/4)cos2x + (1/4)cos4x + (-1/4)cos6x

Lời giải:

Đáp án: B

Ta có: y = (1/2)(cos3x+cosx)cos3x = (1/4)(cos6x+1+cos4x+cos2x)

Khi đó y ’’ = - cos2x - 4cos4x - 9cos6x

Đáp án B

Bài 5: Đạo hàm cấp 2016 của hàm số y = sinx bằng biểu thức nào sau đây?

A. cosx
B. sinx
C. -sinx
D. -cosx

Lời giải:

Đáp án: B

Đáp án B

Ta có:

Vậy đạo hàm cấp 2016 của hàm số đã cho là : sinx

Bài 6: Cho hàm số f(x) = x2015 + 2x2014 + 3x2013 +⋯ + 2015x + 2016. Giá trị f(2016)(x) bằng:

A. 2016!
B. 2015!
C. 2014!
D. 0

Lời giải:

Đáp án: D

Đáp án D

Do số mũ cao nhất trong đa thức x2015 + 2x2014 + 3x2013 +⋯ + 2015x + 2016 là 2015 nên f(2016)(x) = 0

Bài 7: Hàm số có đạo hàm cấp hai là:

Lời giải:

Đáp án: D

Chọn D.

Ta có

Bài 8: Hàm số y = (x2 + 1)3 có đạo hàm cấp ba là:

A. y ''' = 12(x2+1)
B. y ''' = 24(x2+1)
C. y ''' = 24(5x2+3)
D. y ''' = -12(x2+1)

Lời giải:

Đáp án: C

Chọn C.

Ta có y = x6+3x4+3x2+1; y' = 6x5+12x3+6x

y'' = 30x4+36x2+6; y ''' = 120x3+72x = 24x(5x2+3)

Bài 9: Hàm số có đạo hàm cấp hai bằng:

Lời giải:

Đáp án: C

Chọn C

Ta có

Bài 10: Hàm số có đạo hàm cấp 5 bằng:

Lời giải:

Đáp án: A

Chọn A.

Ta có

Bài 11: Hàm số có đạo hàm cấp 5 bằng:

Lời giải:

Đáp án: A

Chọn A.

Ta có:

Bài 12: Hàm số có đạo hàm cấp 2 bằng:

Lời giải:

Đáp án: C

Chọn C.

Bài 13: Hàm số y = (2x+5)5 có đạo hàm cấp 3 bằng:

A. y ''' = 80(2x+5)5
B. y ''' = 480(2x+5)2
C. y ''' = -480(2x+5)2
D. y ''' = -80(2x+5)3

Lời giải:

Đáp án: B

Chọn B.

Ta có: y' = 5(2x+5)4.2 = 10(2x+5)4; y'' = 80(2x+5)3; y ''' = 480(2x+5)2.

Bài 14: Hàm số y = tanx có đạo hàm cấp 2 bằng:

Lời giải:

Đáp án: D

Chọn D

Ta có:

Bài 15: Cho hàm số y = sinx. Chọn câu sai.

Lời giải:

Đáp án: D

Chọn D

Ta có:

Xem thêm các dạng bài tập toán hay khác:

• 30 bài tập về Giới hạn, đạo hàm của hàm số mũ, lũy thừa, lôgarit (2024) có đáp án, cực hay
• 30 bài tập Cách tính đạo hàm của hàm hợp cực hay, chi tiết (2024)
• 70 Bài tập về đạo hàm cấp hai (có đáp án năm 2024) có đáp án