Giải hệ phương trình đôi là một trong những bài toán quan trọng trong học Toán. Phương pháp cộng đại số là một công cụ quan trọng giúp giải quyết các bài toán này một cách nhanh chóng và chính xác. Trong bài viết này, chúng ta sẽ cùng nhau tìm hiểu về phương pháp cộng đại số và giải 50 bài tập giải hệ phương trình bằng phương pháp này.
Kiến thức cần nhớ
1. Quy tắc cộng đại số
Quy tắc cộng đại số là một phương pháp biến đổi một hệ phương trình thành hệ phương trình tương đương. Đây là những bước cơ bản để giải hệ phương trình bằng phương pháp cộng đại số.
Bước 1: Cộng hay trừ từng vế của hai phương trình đã cho để được phương trình mới.
Bước 2: Dùng phương trình mới đó thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia).
Ví dụ 1:
Xét hệ phương trình:
2x - y = 5
3x + y = 10Áp dụng quy tắc cộng đại số để biến đổi hệ phương trình.
Từ phương trình thứ nhất, ta có:
2x - y = 5Từ phương trình thứ hai, ta có:
3x + y = 10Cộng vế với vế của phương trình (1) với phương trình (2) ta được hệ mới:
2x - y + 3x + y = 5 + 10Simplifying the equation, we have:
5x = 15Điều này cho ta biết x = 3.
Substituting the value of x into either of the original equations, we can find the value of y. Let's use the first equation:
2(3) - y = 5
6 - y = 5Simplifying the equation, we have:
y = 6 - 5
y = 1Vậy, hệ phương trình đã cho có nghiệm (x; y) là (3; 1).
2. Giải hệ phương trình bằng phương pháp cộng đại số
a) Trường hợp thứ nhất: Các hệ số của cùng một ẩn nào đó trong hệ phương trình đã bằng nhau hoặc đối nhau
Bước 1: Cộng (trừ) vế với với của hai phương trình ban đầu với nhau để được phương trình mới.
Bước 2: Viết lại hệ phương trình mới với một phương trình là phương trình mới sau khi đã cộng (trừ) đại số và một phương trình là phương trình ban đầu của hệ. Giải hệ phương trình.
Ví dụ 2:
Xét hệ phương trình:
x + 3y = 5
4x + 3y = 11Từ phương trình thứ nhất, ta có:
x + 3y = 5Từ phương trình thứ hai, ta có:
4x + 3y = 11Trừ vế với vế của phương trình (1) cho phương trình (2) ta được hệ phương trình mới:
x + 3y - 4x - 3y = 5 - 11Simplifying the equation, we have:
-3x = -6Điều này cho ta biết x = 2.
Substituting the value of x into either of the original equations, we can find the value of y. Let's use the first equation:
2 + 3y = 5
3y = 5 - 2Simplifying the equation, we have:
3y = 3
y = 1Vậy, hệ phương trình đã cho có nghiệm (x; y) là (2; 1).
b) Trường hợp thứ hai: Các hệ số của mỗi ẩn trong phương trình không bằng nhau hoặc không đối nhau
Bước 1: Nhân hai vế của mỗi phương trình với các số thích hợp sao cho với một ẩn nào đó các hệ số bằng nhau hoặc đối nhau.
Bước 2: Cộng (trừ) vế với với của hai phương trình ban đầu với nhau để được phương trình mới.
Bước 3: Viết lại hệ phương trình mới với một phương trình là phương trình mới sau khi đã cộng (trừ) đại số và một phương trình là phương trình ban đầu của hệ. Giải hệ phương trình.
Ví dụ 3:
Xét hệ phương trình:
2x + 3y = 5
1x + 2y = 7Nhân hai vế của phương trình (1) với 3 và hai vế của phương trình (2) với 2 ta được hệ mới:
6x + 9y = 15
2x + 4y = 14Từ hai phương trình trên, chúng ta có thể thấy rằng hệ số của ẩn y đã trở thành 9 và 4. Ta có thể tiếp tục giải hệ phương trình mới này bằng cách cộng hoặc trừ các phương trình này với nhau.
Bài tập tự luyện
Bài 1: Giải các hệ phương trình sau bằng phương pháp cộng đại số:
x + 3y = 5
2x - y = 1Lời giải: (Các phần giải thích học sinh không phải trình bày).
(Vì hệ số của y ở 2 phương trình đối nhau nên cộng từng vế của 2 phương trình).
Vậy hệ phương trình có nghiệm duy nhất (2; -3).
(Hệ số của x ở 2 phương trình bằng nhau nên ta trừ từng vế của 2 phương trình)
Vậy hệ phương trình có nghiệm duy nhất
(Nhân cả hai vế của phương trình 2 với 2 để hệ số của x bằng nhau)
(Hệ số của x bằng nhau nên ta trừ từng vế của 2 phương trình)
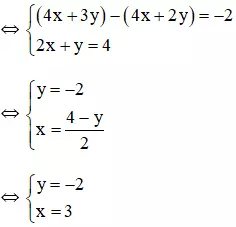Vậy hệ phương trình có nghiệm duy nhất (3; -2).
(Nhân hai vế phương trình 1 với 2 để hệ số của y đối nhau)
(Hệ số của y đối nhau nên cộng từng vế hai phương trình)
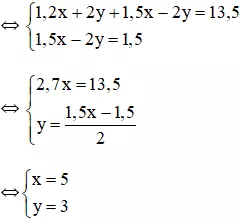Vậy hệ phương trình có nghiệm duy nhất (-1; 0).
(Nhân hai vế phương trình 1 với 4 để hệ số của y đối nhau)
(Hệ số của y đối nhau nên ta cộng từng vế 2 phương trình)
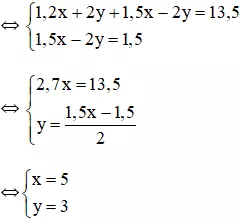Vậy hệ phương trình có nghiệm duy nhất (5; 3).
Bài 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:
x^2 − 3y = 1
2x^6 − y^2 = 2Lời giải: a) x^2 − 3y = 1
⇔ 2x^6 − y^2 = 2 (nhân cả hai vế phương trình thứ nhất với 2)
⇔ 2x^6 − y^2 = 2
b) 5x^3 + y = 2
⇔ 2x^6 − y^2 = 2
Vậy hệ phương trình đã cho có nghiệm (x; y) = (2/3; −2/3).
Bài 3: Giải các hệ phương trình sau bằng phương pháp cộng đại số:
x^2 − 3y = 1
2x^6 − y^2 = 2Lời giải: a) Đặt x + y = u và x - y = v (*)
Khi đó hệ phương trình trở thành
u - v = 1
u + v = 6Thay u = 3 và v = 2 vào (*) ta được hệ phương trình:
x + y = 3
x - y = 2Vậy hệ phương trình đã cho có nghiệm (x; y) = (2.5; 0.5).
Với những kiến thức vừa học, bạn đã có thể giải 50 bài tập giải hệ phương trình bằng phương pháp cộng đại số một cách thành thạo. Hãy tiếp tục rèn luyện và ứng dụng kiến thức này vào giải các bài toán thực tế khác. Chúc bạn thành công!
