Nguyên hàm và cách giải bài tập cơ bản - Toán lớp 12
A. LÝ THUYẾT.
1. Khái niệm nguyên hàm.
- Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x thuộc K. F'(x) = f(x), ∀x ∈ K
Định lí:
- Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
- Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số. Do đó F(x) + C, C ∈ ℝ là họ tất cả các nguyên hàm của f(x) trên K.
2. Tính chất của nguyên hàm.
- Nếu F(x) có đạo hàm thì: ∫dF(x) = F(x) + C
- ∫k.f(x)dx = k∫f(x)dx với k là hằng số khác 0.
- ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
3. Sự tồn tại của nguyên hàm.
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
4. Bảng nguyên hàm các hàm số thường gặp.

B. CÁC DẠNG BÀI TOÁN HAY GẶP VÀ VÍ DỤ.
Phương pháp giải: Áp dụng các công thức nguyên hàm cơ bản đã nêu ở phần lý thuyết để giải các bài toán sau.
Bài toán 1: Tìm nguyên hàm F(x) của hàm số f(x) trên D ⊂ ℝ. Ví dụ 1: Cho hàm số f(x) = x^2 + 3. Khẳng định nào sau đây đúng? A. ∫f(x)dx = x^2 + 3x + C B. ∫f(x)dx = x^3/3 + 3x + C C. ∫f(x)dx = x^3 + 3x + C D. ∫f(x)dx = 2x + C
Lời giải: ∫f(x)dx = ∫(x^2 + 3)dx = ∫x^2dx + ∫3dx = x^3/3 + 3x + C
Chọn B.
Bài toán 2: Tìm F(x) là một nguyên hàm của f(x) trên D ⊂ ℝ. Ví dụ 2: Cho F(x) = 16.ln(x) - 3x + 3 + 1/12. Hỏi F(x) là nguyên hàm của hàm số nào dưới đây? A. f(x) = 1/x^2 - 9 B. f(x) = 1/x - 9 C. f(x) = 1/x^2 - 9 + x^(-1/2) D. f(x) = 1/x^2 + 9 + x^(-1/2)
Lời giải:
Ta có:
Chọn A.
Bài toán 3: Xác định nguyên hàm của một hàm số với điều kiện cho trước. Ví dụ 3: Cho hàm số f(x) thỏa mãn f'(x) = 3 - 5sin(x) và f(0) = 10. Mệnh đề nào dưới đây đúng? A. f(x) = 3x + 5cos(x) + 5 B. f(x) = 3x + 5cos(x) + 2 C. f(x) = 3x - 5cos(x) + 2 D. f(x) = 3x - 5cos(x) + 15
Lời giải:

Chọn A.
Bài toán 4: Tìm giá trị của tham số để F(x) là một nguyên hàm của f(x). Ví dụ 4: Cho kết quả của ∫(x^2 + 2x^3)dx có dạng a^3x^3 + b^4x^4 + C, trong đó a, b là hai số hữu tỉ. Giá trị a bằng: A. 2 B. 1 C. 9 D. 32
Lời giải: Theo đề, ta cần tìm ∫(x^2 + 2x^3)dx. Sau đó, ta xác định giá trị của a. Ta có: ∫(x^2 + 2x^3)dx = ∫x^2dx + 2∫x^3dx = 1/3x^3 + 2/4x^4 + C Suy ra để ∫(x^2 + 2x^3)dx có dạng a^3x^3 + b^4x^4 + C thì a = 1, b = 2.
Chọn B.
C. BÀI TẬP TỰ LUYỆN.
Câu 1. Nguyên hàm của hàm số f(x) = x^3 + x là A. x^4 + x^2 + C. B. 1/3x^2 + 1/2x + C. C. x^3 + x + C. D. 1/4x^4 + 1/2x^2 + C.
Câu 2. Nguyên hàm của f(x) = x^3 - x^2 + 2x là: A. 1/4x^4 - x^3 + 4/3x^3 + C. B. 1/4x^4 - 1/3x^3 + 4/3x^3 + C. C. 1/4x^4 - x^3 + 2/3x^3 + C. D. 1/4x^4 - 1/3x^3 + 2/3x^3 + C.
Câu 3. Nguyên hàm của f(x) = 1/x + 2x^3 + 3 là: A. 2x + 3x^2 + 3x + C. B. 2x + 4/3x^2 + 3x + C. C. 1/2x + 3/2x^2 + 3x + C. D. 1/2x + 4/3x^2 + 3x + C.
Câu 4. Hàm số f(x) có nguyên hàm trên K nếu: A. fx xác định trên K. B. fx có giá trị lớn nhất trên K C. fx có giá trị nhỏ nhất trên K D. fx liên tục trên K
Câu 5. Mệnh đề nào sau đây sai? A. Nếu F(x) là một nguyên hàm của f(x) trên [a, b] và C là hằng số thì ∫f(x)dx = F(x) + C. B. Mọi hàm số liên tục trên [a, b] đều có nguyên hàm trên [a, b]. C. F(x) là một nguyên hàm của f(x) trên [a, b] ⇔ F'(x) = f(x), ∀x ∈ [a, b] D. ∫f(x)dx' = f(x)
Câu 6. Gọi F(x) là nguyên hàm của hàm số f(x) = 4x^3 + 2m^(-1)x + m + 5, với m là tham số thực. Tìm một nguyên hàm của f(x) biết rằng F(1) = 8 và F(0) = 1. A. F(x) = x^4 + 2x^2 + 6x + 1 B. F(x) = x^4 + 6x + 1. C. F(x) = x^4 + 2x^2 + 1. D. Đáp án A và B.
Câu 7. Họ nguyên hàm của I = ∫e^x dx là: A. 2e^x + C. B. e^x. C. e^(2x) + C. D. e^x + e^x + C.
Câu 8. Cho ∫(2a + 1)x^3 + bx^2 dx, trong đó a, b là hai số hữu tỉ. Biết rằng ∫(2a + 1)x^3 + bx^2 dx = 3/4x^4 + x^3 + C. Giá trị a, b lần lượt bằng: A. 1; 3. B. 3; 1. C. -1/8; 1. D. 2; 4.
Câu 9. Tính ∫(2 + e^(3x))^2 dx A. 3x + 4/3e^(3x) + 16/3e^(6x) + C. B. 4x + 4/3e^(3x) + 5/6e^(6x) + C. C. 4x + 4/3e^(3x) - 16/3e^(6x) + C. D. 4x + 4/3e^(3x) + 16/3e^(6x) + C.
Câu 10. Nguyên hàm của hàm số f(x) = x^2 - 3x + 1/x là: A. x^(4/4) - 3x^2/(2.2) - ln|x| + C. B. x^(3/3) - 3x^(2/2) + ln|x| + C. C. x^(4/4) - 3x^2/(2.2) + ln|x| + C. D. x^(3/3) + 3x^(2/2) + ln|x| + C.
Câu 11. Nguyên hàm của hàm số y = 3x - 1 trên [1/3;+∞] là: A. 3/2x^2 - x + 2 + C. B. 2/9x - 1/3 + C. C. 3/2x^2 - x + 2 + C. D. 19/3x - 1/3 + C.
Câu 12. Hàm số F(x) = e^x + e^(-x) + x là một nguyên hàm của hàm số nào sau đây? A. f(x) = e^(-x) + e^x + 1. B. f(x) = e^x - e^(-x) + 1/2x^2. C. f(x) = e^x - e^(-x) + 1. D. f(x) = e^x + e^x + 1/2x^2.
Câu 13. Tính ∫2x + 1 dx. A. 2x + 1ln(2) + C. B. 2x + 1 + C. C. 3.2x + 1ln(2) + C. D. 2x + 1ln(2) + C.
Câu 14. Tính ∫(x^2 - 3x + 1/x) dx. A. x^3 - 3x^2 + ln|x| + C. B. x^(3/3) - 3x^(2/2) + ln|x| + C. C. x^(3/3) - 3x^(2/2) + 1/x^2 + C. D. x^(3/3) - 3x^(2/2) + ln|x| + C.
Câu 15. Tính ∫(2x + 1) dx. A. 2x + 1ln(2) + C. B. 2x + 1 + C. C. 3.2x + 1ln(2) + C. D. 2x + 1.ln(2) + C.
Câu 16. Tìm một nguyên hàm F(x) của f(x) = x^3 - 1/x^2 biết F(1) = 0. A. F(x) = x^2/2 - 1/x + 1/2 B. F(x) = x^2/2 + 1/x - 3/2 C. F(x) = x^2/2 - 1/x - 1/2 D. F(x) = x^2/2 + 1/x - 3/2
Câu 17. Tìm hàm số F(x) biết rằng F'(x) = 4x^3 - 3x^2 + 2 và F(-1) = 3. A. F(x) = x^4 - x^3 - 2x - 3 B. F(x) = x^4 - x^3 + 2x + 3 C. F(x) = x^4 - x^3 - 2x + 3 D. F(x) = x^4 + x^3 + 2x + 3
Câu 18. Họ nguyên hàm của hàm số f(x) = 2x + 3x là : A. 4x + 3ln|x| + C. B. 2x + 3ln|x| + C. C. 4x - 1 + 3ln|x| + C. D. 16x - 3ln|x| + C.
Câu 19. Họ nguyên hàm của hàm số f(x) = 4/3x - 2 là : A. 16ln(3x) - 1 + C. B. -1/3ln(3x) - 1 + C. C. -16ln(3x) - 1 + C. D. 4/3ln(3x) - 2 + C.
Câu 20. Họ nguyên hàm của hàm số f(x) = e^x - e^(-x) là : A. e^x + e^(-x) + C. B. e^x - e^(-x) + C. C. -e^x + e^(-x) + C. D. e^x + e^x + C.
Câu 21. Họ nguyên hàm của hàm số f(x) = 3/2x^(-2) - 3x^3.ln(2) là : A. 3/2x^2.ln(3) + 2 - 3/2x^3.ln(2) + C. B. 3/2x^2.ln(3) - 2 - 3/2x^3.ln(2) + C. C. 3 - 2x^2.ln(3) + 2/3x^3.ln(2) + C. D. 3 - 2x^2.ln(3) - 2/3x^3.ln(2) + C.
Câu 22. Nguyên hàm F(x) của hàm số f(x) = x^2 + 1/x^2 là hàm số: A. F(x) = x^(3/3) - 1/x + 2x + C. B. F(x) = x^(3/3) + x + 2x + C. C. F(x) = x^(3/3) + x + x^(2/2) + C. D. F(x) = x^(3/3) + x + x^(2/2) + 3x + C.
Câu 23. Nguyên hàm F(x) của hàm số f(x) = 2x^2 + x^3 - 4 thỏa mãn điều kiện F(0) = 0 là: A. 2x^3 - 4x^4. B. 2/3x^3 + x^4/4 - 4x. C. x^3 - x^4 + 2x. D. Đáp án khác.
Câu 24. Biết F(x) là nguyên hàm của hàm số 1/x - 1 và F(2) = 1. Khi đó F(3) bằng bao nhiêu: A. e + ln(2) B. 1/2 C. ln(3^2) D. ln(2e)
Câu 25. Hàm số f(x) có nguyên hàm trên K nếu A. fx xác định trên K. B. fx có giá trị lớn nhất trên K C. fx có giá trị nhỏ nhất trên K D. fx liên tục trên K
Câu 26. Cho hai hàm số f(x),g(x) là hàm số liên tục, có F(x),G(x) lần lượt là nguyên hàm của f(x),g(x). Xét các mệnh đề sau: (I): F(x) + G(x) là một nguyên hàm của f(x),g(x) (II): k.F(x) là một nguyên hàm của k.f(x) (k∈R) (III): F(x).G(x) là một nguyên hàm của f(x).g(x) Mệnh đề nào là mệnh đề đúng ? A. I B. I và II C. I, II, III D. II
Câu 27. Trong các khẳng định sau khẳng định nào sai? A. ∫0dx = C (là hằng số) B. ∫1xdx = ln|x| + C (là hằng số) C. ∫x^αdx = 1/(α+1)x^(α+1) + C (là hằng số) D. ∫dx = x + C (là hằng số)
Câu 28. ∫[3x - 1]/[3x^2] dx bằng: A. 3xln(3) - ln(3)/3x^2 + C B. 1/(3x)ln(3) - 1/3(3x)^ln(3) + C C. 9x^2ln(3) - 12.9xln(3) - 2x + C D. 1/(2ln(3))x + 1/(9ln(3))x - 2x + C
Câu 29. Trong các khẳng định sau, khẳng định nào sai? A. F(x) = x^2 là một nguyên hàm của f(x) = 2x. B. F(x) = x là một nguyên hàm của f(x) = 2x. C. Nếu F(x) và G(x) đều là nguyên hàm của hàm số f(x) thì F(x) - G(x) = C (hằng số). D. ∫[f1(x) + f2(x)]dx = ∫f1(x)dx + ∫f2(x)dx
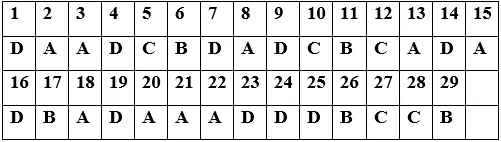
Đáp án [^1^]:

[^1^]: Một số đáp án có thể khác do markdown không hỗ trợ ký tự mũ và ghi chú hình ảnh.












