Tính Chất Ba Đường Cao Của Tam Giác

Đường cao của tam giác

Trong tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện được gọi là đường cao của tam giác đó. Có thể xem đường cao là đường thẳng dọc xuất phát từ đỉnh của tam giác và kết thúc tại đường chứa cạnh đối diện của đỉnh đó. Mỗi tam giác đều có ba đường cao.

Tính chất ba đường cao của tam giác

Theo định lí, ba đường cao của một tam giác cùng đi qua một điểm. Điều này có nghĩa là ba đường cao của tam giác cắt nhau tại một điểm duy nhất.

Về các đường cao, trung tuyến, trung trực, phân giác của tam giác cân

Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường phân giác và đường trung tuyến, cùng xuất phát từ đỉnh đối diện với cạnh đáy. Điều này đồng nghĩa với việc ba đường cao cũng cắt nhau tại một điểm. Như vậy, nếu hai trong bốn loại đường trên trùng nhau, tam giác đó được coi là tam giác cân.

Bài tập luyện tập tính chất ba đường cao của tam giác

Bài 1.

Cho tam giác MNI nhọn, với MN < MI. Các đường cao MA và NB cắt nhau tại H.

1. Chứng minh: H là trực tâm của tam giác MNI.
2. Gọi C là giao điểm của đường thẳng IH và đường thẳng MN. Vẽ điểm D sao cho C là trung điểm của HD. Tam giác MDH là tam giác gì? Vì sao?
3. Chứng minh:

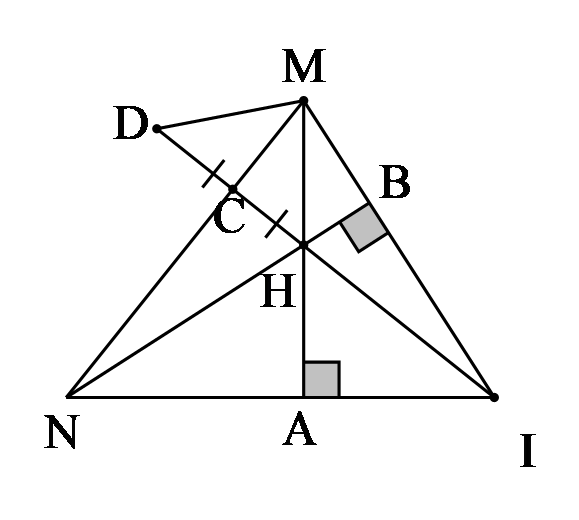
ĐÁP ÁN: a. Tam giác MNI có hai đường cao là NA và MB (giả thiết). H là trực tâm của tam giác MNI. Do đó, HI là đường cao của tam giác MNI.

b. Xét tam giác MHD:

• MC là đường trung trực (C là trung điểm của HD).
• MC là cạnh đáy của tam giác MHD. Vậy tam giác MHD là tam giác cân.

c. Tam giác MHD cân tại M có MC là đường cao cũng như đường phân giác. Ta có: MC = MC (cùng cạnh chung). Vậy tam giác MHC là tam giác cân.

Bài 2.

Cho tam giác DEC vuông tại D (DE < DC). Trên tia ED, lấy điểm B sao cho EB = ED. Đường phân giác của góc E cắt DC tại A và cắt BC tại F. Trên cạnh EC, lấy điểm G sao cho GE = EC. Chứng minh:

1. AG ⊥ EC.
2. Ba điểm A, B, G thẳng hàng.

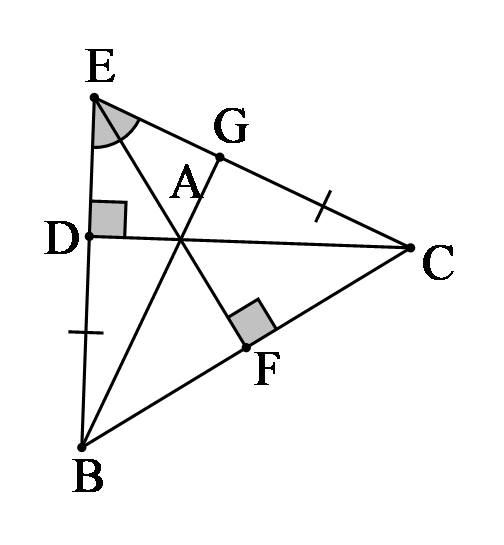
ĐÁP ÁN: a. Ta có:

• Góc DEC = Góc EDC (góc vuông).
• Góc EDA = Góc EAG (đường phân giác chia đôi góc).
• ED = EG (giả thiết). Xét tam giác EAD và EAG:
• ED = EG (chứng minh trên).
• Góc EDA = Góc EAG (đường phân giác).
• Cạnh chung EA.
• Do đó, tam giác EAD và EAG đồng dạng. Vậy, góc DAH = Góc GAH (đồng dạng).

b. Tam giác EBC có EB = EC (giả thiết). Đường phân giác EF chính là đường cao của tam giác EBC. Các đường cao CD và EF cắt nhau tại A. A là trực tâm của tam giác EBC. Do đó, đường AH cũng là đường cao của tam giác EBC. Ta có: AH = AH (cùng phụ với tam giác EBC). Vậy, hai đường thẳng BA và AG trùng nhau. Từ đó, suy ra ba điểm A, B, G thẳng hàng.

Biên soạn: PHẠM NGỌC DIỆU (Trường THCS - THPT Nguyễn Khuyến BD)