Trong lĩnh vực công nghệ thông tin, bài toán tìm đường đi ngắn nhất (Shortest Path Problems) trong đồ thị trọng số không còn xa lạ với sinh viên chuyên ngành này nữa. Trong bài viết này, chúng ta sẽ đi qua 3 nội dung chính:

1. Giới thiệu bài toán tìm đường đi ngắn nhất và ứng dụng của nó

Bài toán tìm đường đi ngắn nhất được minh họa bằng một ví dụ cơ bản như sau:

Bài toán: Cho một đồ thị trọng số gồm các nodes A, B, C, D, E, F và khoảng cách giữa các nodes như hình bên dưới. Tìm đường đi ngắn nhất từ node B đến các node còn lại trong đồ thị?
Xem thêm:

Trở thành kỹ sư lập trình nhúng cần những gì? Học ở đâu tốt nhất?

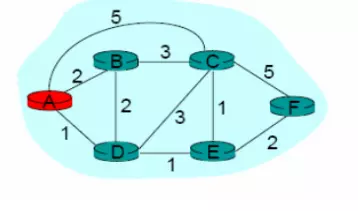
Bài toán tìm đường đi ngắn nhất với giải thuật Dijkstra

Sau khi giải bài toán, ta thu được kết quả như sau. Đường đi ngắn nhất từ A đến 5 node còn lại:

Từ A -> B: A - B, tổng độ dài đường đi = 2
Từ A -> C: A - C, tổng độ dài đường đi = 5
Từ A -> D: A - D, tổng độ dài đường đi = 1
Từ A -> E: A - D - E, tổng độ dài đường đi = 2
Từ A -> F: A - D - E - F, tổng độ dài đường đi = 4

Ứng dụng của việc giải bài toán này rất phổ biến, một ví dụ điển hình là tìm đường đi ngắn nhất trên bản đồ. Thay các node bằng các giao lộ, và các cạnh của đồ thị là các tuyến đường, chúng ta sẽ có một bài toán quen thuộc. Cũng có thể áp dụng giải thuật này để tìm đường đi ngắn nhất trong các hệ thống mạng, nơi các node là các router mạng hoặc các host.

2. Giải thích về giải thuật Dijkstra

Giải thuật Dijkstra hoạt động theo các bước sau:

Bước 1: Chọn tập S = {} là tập các source_node bao gồm current_node và passed_node. Current_node là node đang được xét đến, passed_node là các node đã được xét. Current_node đầu tiên sẽ là node đích của bài toán tìm đường đi ngắn nhất.
Bước 2: Khởi tạo giải thuật với current_node là node đích và cost(N) là giá trị của đường đi ngắn nhất từ N đến node đích.
Bước 3: Xét các node kề N với current_node. Gọi d(current_node, N) là khoảng cách giữa node kề N và current_node. Với p = d(current_node, N) + cost(current_node), nếu p < cost(N) thì cost(N) = p, ngược lại cost(N) giữ nguyên giá trị.
Bước 4: Sau khi xét hết các node kề N, đánh dấu current_node thành passed_node.
Bước 5: Tìm current_node mới với 2 điều kiện: không phải passed_node và cost(current_node) là nhỏ nhất.
Bước 6: Nếu tập S = {} chứa đủ các node của đồ thị thì dừng thuật toán, ngược lại quay trở lại Bước 3.

Để minh họa cách giải thuật Dijkstra hoạt động, chúng ta sẽ sử dụng đồ thị trọng số dưới đây để tìm đường đi ngắn nhất từ node C đến mọi node còn lại trong đồ thị:

Bài toán tìm đường đi ngắn nhất với giải thuật Dijkstra

Trong quá trình thuật toán chạy, ta gọi cost(node) là "khoảng cách ngắn nhất từ mỗi node đến node C" và đánh dấu nó trên hình (giá trị số màu xanh da trời). Khi thuật toán bắt đầu, ta mặc định lưu cost(C) = 0, cost(A) = cost(B) = cost(D) = cost(E) = vô cùng.

Ta cũng đánh dấu current_node (node đang xét hiện tại) bằng một dấu chấm đỏ trên hình. Current_node đầu tiên sẽ là node đích của bài toán - ở đây là C.

Thuật toán bắt đầu bằng cách xét tất cả các node kề với current_node (các node được nối trực tiếp với current_node), ở đây là A, B và D. Ta sẽ bắt đầu với node B trước và thực hiện 4 bước:

Đầu tiên ta tìm được khoảng cách từ current_node đến node B: d(C, B) = 7.
Tính toán giá trị đường đi từ node đích -> current_node -> node B: p = d(C, B) + cost(current_node) = 0 + 7 = 7.
Nếu giá trị vừa tính p < cost(B) thì cost(B) = p, ngược lại giữ nguyên giá trị cost(B) (ở đây 7 < vô cùng nên cost(B) = 7).
Đánh dấu cost(B) lên hình.

Tương tự với A và D, ta cũng tìm được cost(A) = 1 và cost(D) = 2.

Sau khi xét hết tất cả các node kề với current_node, ta chuyển current_node thành passed_node - tức là node đã được xét rồi. Passed_node sẽ được đánh 1 dấu tích xanh trên hình.

Bây giờ chúng ta sẽ chọn 1 current_node mới với 2 điều kiện:

Current_node không thể là passed_node.
Cost(current_node) có giá trị nhỏ nhất.

Nếu xét trên hình, current_node tiếp theo sẽ là node A. Ta đánh dấu node A với 1 dấu chấm đỏ.

Ta tiếp tục giải thuật bằng cách xét các node kề với current_node với điều kiện node kề không được là passed_node. Như vậy ở đây ta chỉ được xét node B.

d(A, B) = 3, cost(A) = 1.
p = d(A, B) + cost(A) = 4.
p < cost(B) (4 < 7). Vậy cost(B) = 4.
Đánh dấu cost(B) lên hình.

Đánh dấu node A trở thành passed_node. Ta tiếp tục tìm current_node mới, lần này nó là node D với cost(D) = 2.

Có 2 node kề với D là B và E.

Xét với node B:

d(D, B) = 5, cost(D) = 2.
p = d(D, B) + cost(D) = 7.
p > cost(B) (7 > 4). Vậy cost(B) giữ nguyên giá trị.

Xét với node E:

d(D, E) = 7, cost(D) = 2.
p = d(D, E) + cost(D) = 9.
p < cost(E) (7 < vô cùng). Vậy cost(E) = 9.
Đánh dấu cost(E) lên hình.

Đánh dấu node D trở thành passed_node. Ta tiếp tục tìm current_node mới, lần này nó là node B với cost(B) = 4.

Chỉ còn 1 node kề với B là E.

Xét với node E:

d(B, E) = 1, cost(B) = 4.
p = d(B, E) + cost(B) = 5.
p < cost(E) (5 < 9). Vậy cost(E) = 5.
Đánh dấu cost(E) lên hình.

Giờ chúng ta không còn node nào để kiểm tra nữa. Đánh dấu node E trở thành passed_node và kết thúc thuật toán.

Vậy ta có kết quả của thuật toán với đường đi ngắn nhất từ C đến các điểm còn lại là:

Từ C -> A: C - A, cost(A) = 1
Từ C -> B: C - A - B, cost(B) = 4
Từ C -> D: C - D, cost(D) = 2
Từ C -> E: C - A - B - E, cost(E) = 5

3. Giải thuật Dijkstra với code Ruby

Việc triển khai giải thuật Dijkstra trong code Ruby khá dễ hiểu. Dưới đây là một đoạn mã Ruby để thực hiện giải thuật này:

class Graph   # Constructor   def initialize     @g = {} # the graph // {node => {edge1 => weight, edge2 => weight}, node2 => ...}     @nodes = Array.new     @INFINITY = 1 << 64   end    def add_edge(s, t, w)     # s = source, t = target, w = weight     if (not @g.has_key?(s))       @g[s] = {t => w}     else       @g[s][t] = w     end      # Begin code for non-directed graph (inserts the other edge too)     if (not @g.has_key?(t))       @g[t] = {s => w}     else       @g[t][s] = w     end     # End code for non-directed graph (i.e. deletme if you want it directed)      if (not @nodes.include?(s))       @nodes << s     end     if (not @nodes.include?(t))       @nodes << t     end   end    # based on wikipedia's pseudocode: http://en.wikipedia.org/wiki/Dijkstra's_algorithm   def dijkstra(s)     @d = {}     @prev = {}     @nodes.each do |i|       @d[i] = @INFINITY       @prev[i] = -1     end      @d[s] = 0     q = @nodes.compact      while (q.size > 0)       u = nil       q.each do |min|         if (not u) or (@d[min] and @d[min] < @d[u])           u = min         end       end        if (@d[u] == @INFINITY)         break       end        q = q - [u]       @g[u].keys.each do |v|         alt = @d[u] + @g[u][v]         if (alt < @d[v])           @d[v] = alt           @prev[v] = u         end       end     end   end    # To print the full shortest route to a node   def print_path(dest)     if @prev[dest] != -1       print_path @prev[dest]     end     print ">#{dest}"   end    # Gets all shortest paths using Dijkstra   def shortest_paths(s)     @source = s     dijkstra s      puts "Source: #{@source}"      @nodes.each do |dest|       puts "Target: #{dest}"        if @d[dest] != @INFINITY         print_path dest         puts "\nDistance: #{@d[dest]}"       else         puts "NO PATH"       end     end   end end  gr = Graph.new gr.add_edge("a", "b", 5) gr.add_edge("b", "c", 3) gr.add_edge("c", "d", 1) gr.add_edge("a", "d", 10) gr.add_edge("b", "d", 2) gr.add_edge("f", "g", 1)  gr.shortest_paths("a")

Chúng ta có thể chạy đoạn mã trên trong terminal:

Bài viết của mình còn thiếu sót, mong nhận được nhiều phản hồi tích cực từ các bạn.  ---  Tham khảo: - [https://gist.github.com/yaraki/1730288](https://gist.github.com/yaraki/1730288) - [https://en.wikipedia.org/wiki/Dijkstra's_algorithm](https://en.wikipedia.org/wiki/Dijkstra's_algorithm)