Trong lập trình máy tính, một phép toán bitwise hoạt động trên chuỗi bit, mảng bit hoặc số nhị phân (được coi là một chuỗi bit) trên cấp độ từng bit. Đây là một hoạt động nhanh và đơn giản, cơ bản cho các phép toán số học cấp cao và được hỗ trợ trực tiếp bởi bộ xử lý. Hầu hết các phép toán bitwise được trình bày dưới dạng các chỉ thị hai toán hạng, trong đó kết quả thay thế một trong các toán hạng đầu vào.
Trên các bộ xử lý giá trị thấp đơn giản, phép toán bitwise thường nhanh hơn phép chia, nhiều lần nhanh hơn phép nhân và đôi khi nhanh hơn nhiều so với phép cộng. Trong khi các bộ xử lý hiện đại thông thường thực hiện phép cộng và phép nhân cũng nhanh như phép toán bitwise do độ dài của pipeline hướng dẫn dài hơn và những lựa chọn thiết kế kiến trúc khác, phép toán bitwise thường sử dụng ít công suất hơn do sự giảm thiểu việc sử dụng tài nguyên.
Các toán tử Bitwise
Trong các giải thích dưới đây, bất kỳ chỉ thị nào của một bit đều được tính từ phía bên phải (tức là phía không quan trọng nhất), tiến lên bên trái. Ví dụ, giá trị nhị phân 0001 (thập phân 1) có các số không ở mọi vị trí ngoại trừ vị trí đầu tiên (tức là vị trí bên phải nhất).
Phủ định
NOT, hoặc phủ định bitwise, là một hoạt động số đơn vị thực hiện phủ định logic trên mỗi bit, tạo thành phần bù một giá trị nhị phân đã được cho. Bit bằng 0 trở thành 1 và những bit bằng 1 trở thành 0. Ví dụ:
NOT 0111 (thập phân 7) = 1000 (thập phân 8)
NOT 10101011 (thập phân 171) = 01010100 (thập phân 84)
Kết quả bằng giá trị bù hai của giá trị trừ đi một. Nếu sử dụng phép toán bù hai, thì NOT x = -x - 1.
Đối với các số nguyên không dấu, phần bù của một số là "phản ảnh đối xứng" của số đó qua điểm "giữa chừng" của phạm vi số nguyên không dấu. Ví dụ, đối với các số nguyên không dấu 8-bit, NOT x = 255 - x, điều này có thể được xem như là một đường xuống đơn giản nhưng minh họa để "lật" một phạm vi tăng từ 0 đến 255 thành một phạm vi giảm từ 255 đến 0. Một ví dụ đơn giản nhưng có tính chỉ dẫn là đảo ngược một hình ảnh xám mà mỗi pixel được lưu trữ dưới dạng một số nguyên không dấu.
AND
BITWISE AND là một hoạt động nhị phân mà mỗi cặp bit tương ứng của các biểu diễn nhị phân cùng chiều dài và thực hiện phép toán AND logic trên từng cặp bit tương ứng. Do đó, nếu cả hai bit trong vị trí so sánh đều bằng 1, thì bit trong biểu diễn nhị phân kết quả cũng là 1 (1 x 1 = 1); nếu không, kết quả sẽ là 0 (1 × 0 = 0 và 0 × 0 = 0). Ví dụ:
0101 (thập phân 5) AND 0011 (thập phân 3) = 0001 (thập phân 1)Phép toán này có thể được sử dụng để xác định xem một bit cụ thể là được thiết lập (1) hoặc được xóa (0). Ví dụ, với mẫu bit 0011 (thập phân 3), để xác định xem bit thứ hai được thiết lập chúng ta sử dụng phép AND bitwise với mẫu có giá trị 1 chỉ trong bit thứ hai:
0011 (thập phân 3) AND 0010 (thập phân 2) = 0010 (thập phân 2)Bởi vì kết quả 0010 không phải là số không, chúng ta biết rằng bit thứ hai trong mẫu ban đầu đã được thiết lập. Đây thường được gọi là "bit masking". (Từ đồng nghĩa, việc sử dụng băng keo mặt tránh, hoặc mask, các phần không được thay đổi hoặc các phần không được quan tâm. Trong trường hợp này, các giá trị 0 mask các bit không được quan tâm.)
Bitwise AND có thể được sử dụng để xóa các bit được chọn (hoặc cờ) của một thanh ghi trong đó mỗi bit đại diện cho một trạng thái Boolean cá nhân. Kỹ thuật này là một cách hiệu quả để lưu trữ một số giá trị Boolean bằng cách sử dụng ít bộ nhớ nhất có thể. Ví dụ, 0110 (thập phân 6) có thể được coi là một tập hợp bốn cờ, trong đó cờ thứ nhất và cờ thứ tư được xóa (0), và cờ thứ hai và cờ thứ ba được thiết lập (1). Cờ thứ ba có thể bị xóa bằng cách sử dụng phép AND bitwise với mẫu chứa số 0 chỉ trong cờ thứ ba:
0110 (thập phân 6) AND 1011 (thập phân 11) = 0010 (thập phân 2)Vì thuộc tính này, việc kiểm tra tính chẵn lẻ của một số nhị phân rất dễ dàng bằng cách kiểm tra giá trị của bit có giá trị thấp nhất. Sử dụng ví dụ trên:
0110 (thập phân 6) AND 0001 (thập phân 1) = 0000 (thập phân 0)Vì 6 AND 1 là không, 6 chia hết cho 2 và do đó là số chẵn.
OR
BITWISE OR là một phép toán nhị phân mà mỗi cặp bit tương ứng của các biểu diễn nhị phân cùng chiều dài được thực hiện phép toán OR bao hàm logic trên mỗi cặp bit tương ứng. Kết quả ở mỗi vị trí bằng 0 nếu cả hai bit đều bằng 0, trong khi ngược lại kết quả bằng 1. Ví dụ:
0101 (thập phân 5) OR 0011 (thập phân 3) = 0111 (thập phân 7)Phép toán OR có thể được sử dụng để thiết lập các bit đã chọn của thanh ghi đã được mô tả ở trên. Ví dụ, bit thứ tư của 0010 (thập phân 2) có thể được đặt bằng cách thực hiện phép OR bitwise với mẫu có giá trị 1 chỉ trong bit thứ tư:
0010 (thập phân 2) OR 1000 (thập phân 8) = 1010 (thập phân 10)XOR
BITWISE XOR là một phép toán nhị phân mà mỗi cặp bit tương ứng của các biểu diễn nhị phân cùng chiều dài thực hiện phép toán XOR logic trên từng cặp bit tương ứng. Kết quả ở từng vị trí là 1 nếu chỉ có một trong hai bit tương ứng là 1, nhưng sẽ là 0 nếu cả hai bit đều bằng 0 hoặc cả hai đều bằng 1. Điều này thể hiện sự so sánh giữa hai bit, bằng 1 nếu hai bit khác nhau và bằng 0 nếu hai bit giống nhau. Ví dụ:
0101 (thập phân 5) XOR 0011 (thập phân 3) = 0110 (thập phân 6)Phép toán XOR có thể được sử dụng để đảo ngược các bit đã chọn trong một thanh ghi (còn được gọi là chuyển đổi hoặc flip). Bất kỳ bit nào cũng có thể được chuyển đổi bằng cách XOR nó với 1. Ví dụ, sau khi thực hiện phép XOR với mẫu có giá trị 1 chỉ trong các bit thứ hai và thứ tư của 0010 (thập phân 2), chúng ta có:
0010 (thập phân 2) XOR 1010 (thập phân 10) = 1000 (thập phân 8)Kỹ thuật này có thể được sử dụng để xử lý các mẫu bit đại diện cho các tập hợp trạng thái Boolean. Các lập trình viên mã hợp ngữ và các trình biên dịch tối ưu hóa đôi khi sử dụng XOR như một phím tắt để đặt giá trị của một thanh ghi thành không. Thực hiện XOR trên một giá trị so với chính nó luôn cho kết quả bằng không và trên nhiều kiến trúc, hoạt động này yêu cầu ít chu kỳ đồng hồ hơn và ít bộ nhớ hơn so với việc tải một giá trị bằng không và lưu nó vào thanh ghi.
Nếu tập các chuỗi bit của độ dài cố định n (tức là từ ngôn ngữ máy) được coi như một không gian vector n chiều F2n {displaystyle {bf {F}}{2}^{n}} qua trường F2 {displaystyle {bf {F}}{2}}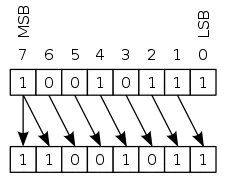 
, thì việc cộng vector tương ứng tương ứng với phép XOR bitwise.
Tổng quan về nhị phân
Có 16 hàm chân trị có thể có của hai biến nhị phân; điều này xác định một bảng chân trị. Dưới đây là các phép toán tương ứng của hai bit P và Q:
p q F0 NO1 Xq2 ¬p3 ↛4 ¬q5 XOR6 NAND7 AND8 XNOR9 q10 If/K11 p12 Then/K13 OR14 T15
1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1Điều này giúp giải thích các phép toán bitwise tương ứng của hai bit P và Q:
- P NOR Q = ¬(P ∨ Q) = ¬P ∧ ¬Q
- P XNOR Q = ¬(P ⊕ Q) = P ∨ Q
- P AND Q = P ∗ Q
- P NAND Q = ¬(P ∧ Q) = ¬P ∨ ¬Q
- P OR Q = P + Q
- P IF/THEN Q = P ∨ Q = Q IF P
- P THEN/IF Q = P ∨ Q = P IF Q
Các phép dịch bit
Các phép dịch bit có thể được coi là các phép toán bitwise vì chúng xử lý giá trị như một chuỗi bit thay vì một số lượng số học. Trong các phép toán này, các chữ số được di chuyển hoặc "dịch" sang trái hoặc phải. Các thanh ghi trong bộ xử lý máy tính có độ rộng cố định, do đó một số bit sẽ "dịch ra" khỏi thanh ghi ở một đầu, trong khi cùng số lượng bit "dịch vào" từ đầu kia; sự khác biệt giữa các phép toán dịch bit nằm ở cách chúng xác định giá trị của các bit được dịch vào.
Dịch trái
Trong một phép dịch trái, các bit ở bên phải được thay thế bằng các bit 0. Trong một phép dịch trái, một số bit được dịch ra (có thể là dấu lớn nhất nếu đang sử dụng bù hai) và một số bit mới được sao chép vào vị trí bên trái, duy trì dấu của toán hạng.
Dịch phải
Trong một phép dịch phải, các bit 0 được dịch vào thay thế các bit bị loại bỏ. Do đó, phép dịch phải logic chèn các giá trị bit 0 vào bit đại diện số hiệu, thay vì sao chép bit dấu. Kết quả là hoạt động này lý tưởng cho các số nguyên không dấu, trong khi phép dịch phải số học lý tưởng cho các số nguyên bù hai có dấu.
Dịch tròn
Một hình thức khác của phép dịch được gọi là dịch tròn, xoay hoặc xoay bit. Trong phép toán này, các bit "được dịch" như cách hai đầu của thanh ghi được nối lại. Giá trị được dịch vào (ở cả hai đầu) trở thành giá trị của cờ nhớ cũ, và bit được dịch ra (ở đầu kia) trở thành giá trị cờ nhớ mới.
Dịch qua cờ nhớ
Dịch qua cờ nhớ là một biến thể của phép dịch, trong đó bit được dịch vào (ở cả hai đầu) là giá trị cũ của cờ nhớ, và bit được dịch ra (ở đầu kia) trở thành giá trị mới của cờ nhớ.
Một lần dịch qua cờ nhớ duy nhất có thể mô phỏng một phép dịch về một vị trí bằng cách thiết lập trước cờ nhớ. Ví dụ, nếu cờ nhớ chứa 0, thì x DỊCH-QUA-CỜ-NHỚ-BỞI-MỘT là một phép dịch qua phải logic, và nếu cờ nhớ chứa một bản sao của bit dấu, thì x DỊCH-QUA-CỜ-NHỚ-BỞI-MỘT là phép dịch qua phải số học.
Vì phép dịch qua cờ nhớ, một giá trị tuyệt đối có thể mô phỏng một phép dịch phải một vị trí bằng cách thiết lập trước cờ nhớ. Ví dụ, nếu giá trị ban đầu của cờ nhớ là 0, thì x DỊCH-QUA-CỜ-NHỚ-BỞI-MỘT là một phép dịch qua trái logic, và nếu cờ nhớ chứa một bản sao của bit dấu, thì x DỊCH-QUA-CỜ-NHỚ-BỞI-MỘT là phép dịch qua trái số học.
Vì dịch qua cờ nhớ, điều này hữu ích khi thực hiện các phép dịch trên số lượng bit lớn hơn kích thước từ gốc của bộ xử lý, vì nếu một số lớn được lưu trữ trong hai thanh ghi, bit bị dịch ra một đầu của thanh ghi đầu tiên phải được di chuyển vào đầu thanh ghi thứ hai. Với dịch qua cờ nhớ, bit này được "lưu giữ" trong cờ nhớ trong lần dịch đầu tiên, sẵn sàng dịch vào trong lần dịch thứ hai mà không cần chuẩn bị bổ sung nào.
Trong các ngôn ngữ lập trình bậc cao
Trong gia đình ngôn ngữ C
Trong các ngôn ngữ C và C++, toán tử dịch trái là "<<", toán tử dịch phải là ">>", và số lượng bit cần dịch được cung cấp dưới dạng đối số thứ hai của toán tử. Ví dụ:
x = y << 2;thiết lập giá trị của x bằng kết quả của việc dịch y sang trái hai bit, tương đương với việc nhân y với bốn.
Các phép dịch có thể dẫn đến hành vi được định nghĩa bởi người triển khai hoặc hành vi không xác định, vì vậy cần thận trọng khi sử dụng chúng. Kết quả của việc dịch một số lượng bit lớn hơn hoặc bằng kích thước từ là hành vi không xác định trong C và C++.[2][3] Việc dịch phải một giá trị âm được định nghĩa bởi người triển khai và không được khuyến nghị bởi các quy tắc viết mã tốt;[4] kết quả của việc dịch trái một giá trị có dấu là không xác định nếu kết quả không thể được biểu diễn trong kiểu kết quả.[2]
Trong C#, việc dịch phải là một phép dịch số học khi toán hạng đầu tiên là một int hoặc long. Nếu toán hạng đầu tiên là uint hoặc ulong, việc dịch phải là một dịch phải logic.[5]
Dịch tròn
Dịch tròn là một biến thể của phép dịch, trong đó giá trị bit được dịch vào (ở cả hai đầu) là giá trị cũ của cờ tròn, và bit được dịch ra (ở đầu kia) trở thành giá trị mới của cờ tròn.
Dịch qua cờ tròn
Dịch qua cờ tròn là một biến thể của phép dịch, trong đó bit được dịch vào (ở cả hai đầu) là giá trị cũ của cờ tròn, và bit được dịch ra (ở đầu kia) trở thành giá trị mới của cờ tròn.
Một lần dịch qua cờ tròn duy nhất có thể mô phỏng một phép dịch qua vị trí bằng cách để trước cờ tròn. Ví dụ, nếu cờ tròn chứa 0, thì x DỊCH-QUA-CỜ-TRÒN-BỞI-MỘT là một phép dịch qua phải logic, và nếu cờ tròn chứa một bản sao của bit dấu, thì x DỊCH-QUA-CỜ-TRÒN-BỞI-MỘT là một phép dịch qua phải số học.
Vì dịch qua cờ tròn, giá trị này có thể mô phỏng một phép dịch qua trái một vị trí bằng cách để trước cờ tròn. Ví dụ, nếu giá trị ban đầu của cờ tròn là 0, thì x DỊCH-QUA-CỜ-TRÒN-BỞI-MỘT là một phép dịch qua trái logic, và nếu cờ tròn chứa một bản sao của bit dấu, thì x DỊCH-QUA-CỜ-TRÒN-BỞI-MỘT là một phép dịch qua trái số học.
Vì dịch qua cờ tròn, cụ thể đại diện cho một phép dịch qua một vị trí có thể được mô phỏng bằng cách sử dụng cờ tròn. Xem ví dụ trước:
x = y DỊCH-QUA-CỜ-TRÒN-BỞI-MỘT;đặt x bằng kết quả của việc dịch y qua một vị trí, tương đương với việc nhân y với hai.
Vì dịch qua cờ tròn, x DỊCH-QUA-CỜ-TRÒN-BỞI-1 có thể mô phỏng một phép dịch qua trái một vị trí bằng cách sử dụng cờ tròn. Ví dụ, xác định xem bit thấp nhất của một số có bằng không hay không có thể được thực hiện bằng cách sử dụng XOR bitwise với cờ tròn:
x = x XOR (x DỊCH-QUA-CỜ-TRÒN-BỞI-1);Nếu x ban đầu bằng 0, thì sau một vòng lặp duy nhất, x sẽ bằng 1 nếu số ban đầu có bit thấp nhất bằng 1 và bằng 0 nếu không có.
Vì dịch qua cờ tròn, điều này hữu ích khi thực hiện các phép dịch trên số lượng bit lớn hơn kích thước từ gốc của bộ xử lý, vì nếu số lớn được lưu trữ trong hai thanh ghi, bit bị dịch ra một đầu của thanh ghi đầu tiên phải được di chuyển vào đầu thanh ghi thứ hai. Với dịch qua cờ tròn, bit này được "lưu giữ" trong cờ tròn trong lần dịch đầu tiên, sẵn sàng dịch vào trong lần dịch thứ hai mà không cần chuẩn bị bổ sung nào.
Trong Java
Trong Java, tất cả các kiểu số nguyên đều có dấu, vì vậy các toán tử "<<" và ">>" thực hiện các phép dịch số học. Java thêm toán tử ">>>" để thực hiện các phép dịch qua phải logic, nhưng vì phép dịch qua trái hợp lệ cho số nguyên có dấu tương tự với phép dịch qua trái số học, không có toán tử "<<<" trong Java.
Chi tiết hơn về toán tử dịch trong Java:[10]
- Các toán tử << (dịch qua trái), >> (dịch qua phải đã ký) và >>> (dịch qua phải không ký) được gọi là các toán tử dịch.
- Kiểu biểu thức dịch là kiểu thăng cấp của toán hạng bên trái.
- Nếu kiểu thăng cấp của toán hạng bên trái là int, chỉ có năm bit hàng đầu của toán hạng bên phải được sử dụng làm khoảng dịch. Nó giống như toán tử AND AND bằng cắt 0x1f (0b11111).[11] Khoảng cách dịch thực sự được sử dụng nằm trong khoảng từ 0 đến 31, bao gồm.
- Nếu kiểu thăng cấp của toán hạng bên trái là long, thì chỉ có sáu bit hàng đầu của toán hạng bên phải được sử dụng làm khoảng dịch. Giống như toán tử AND 0x3f (0b111111).[11] Khoảng cách dịch thực sự được sử dụng nằm trong khoảng từ 0 đến 63, bao gồm.
- Giá trị của n >>> s là n dịch sang phải s bit với sự mở rộng 0.
- Trong các phép toán bit và dịch bit, kiểu byte được chuyển đổi ngầm định thành int. Nếu giá trị byte là âm, bit cao nhất là một, sau đó những người được sử dụng để điền đến những byte bổ sung trong int. Vì vậy, byte b1 = -5; int i = b1 | 0x0200; sẽ cho kết quả i == -5.
Trong Pascal
Trong Pascal, cũng như tất cả các dialekt của nó (chẳng hạn như Object Pascal và Pascal tiêu chuẩn), các toán tử dịch trái và dịch phải được gọi là "shl" và "shr" tương ứng. Ngay cả đối với số nguyên có dấu, shr hoạt động như một dịch phải trong logic, và không sao chép bit dấu. Số bit cần dịch được cung cấp dưới dạng đối số thứ hai. Ví dụ:
x := y shl 2;đặt x bằng kết quả của việc dịch y sang trái hai bit, tương đương với việc nhân y với bốn.
Dịch bit có thể dẫn đến hành vi được định nghĩa bởi người triển khai hoặc hành vi không xác định, nên cần cẩn thận khi sử dụng chúng. Kết quả của việc dịch số lượng bit lớn hơn hoặc bằng kích thước từ gốc là hành vi không xác định trong Pascal.[1]
Dịch trái
Phép toán dịch trái bằng kí tự 'shl', cú pháp như sau:
x := y shl n;trong đó x là biến nhận giá trị sau khi dịch, y là giá trị cần dịch và n là số lượng bit dịch.
Dịch phải
Phép toán dịch phải bằng kí tự 'shr', cú pháp như sau:
x := y shr n;trong đó x là biến nhận giá trị sau khi dịch, y là giá trị cần dịch và n là số lượng bit dịch.
Định vị bit
Để xác định bit thứ n của một số, ta có thể sử dụng phép toán AND bitwise. Ví dụ:
bit := number and (1 shl n);trong đó number là số cần xác định bit, n là vị trí của bit cần xác định.
Trên đây là một số khái niệm cơ bản về bitwise operation trong lập trình máy tính. Hi vọng rằng thông qua bài viết này, bạn có cái nhìn sâu hơn về các phép toán này và tầm quan trọng của chúng khi lập trình.
