Bài viết này sẽ cung cấp cho bạn kiến thức quan trọng về căn bậc 3 trong chương trình Toán lớp 9. Những kiến thức này thường xuyên xuất hiện trong các đề thi học kỳ và thi vào lớp 10. Chúng ta hãy cùng tìm hiểu!
A. Lý thuyết về căn bậc 3 - Toán lớp 9
1. Định nghĩa về căn bậc 3
Căn bậc ba của một số thực hay một biểu thức là x (x là số thực) hoặc X (X là biểu thức) khi và chỉ khi a³ = x hoặc A³ = X. Khi đó, chúng ta sẽ ký hiệu:
- ∛x = a (với x và a là số thực)
- ∛X = A (với X và A là biểu thức)
Số 3 trong căn bậc 3 được gọi là chỉ số căn. Phép lấy căn bậc ba được gọi là phép khai căn bậc ba. Ví dụ: ∛27 = 3 vì 3³ = 27.
Lưu ý: Mỗi số thực a chỉ có duy nhất một căn bậc 3 và căn bậc 3 luôn thỏa mãn các điều kiện sau:
- Nếu a > 0 ⇒ ∛a > 0
- Nếu a < 0 ⇒ ∛a < 0
- Nếu a = 0 ⇒ ∛a = 0
2. Điều kiện của căn bậc 3
Khác với căn bậc 2, căn bậc 3 không yêu cầu nhân tố trong căn phải lớn hơn hoặc bằng 0. Điều này có nghĩa là căn bậc 3 có thể là số âm hoặc số dương tùy ý. Tùy từng dạng bài, điều kiện và tập xác định sẽ khác nhau.
3. Một số tính chất của căn bậc 3
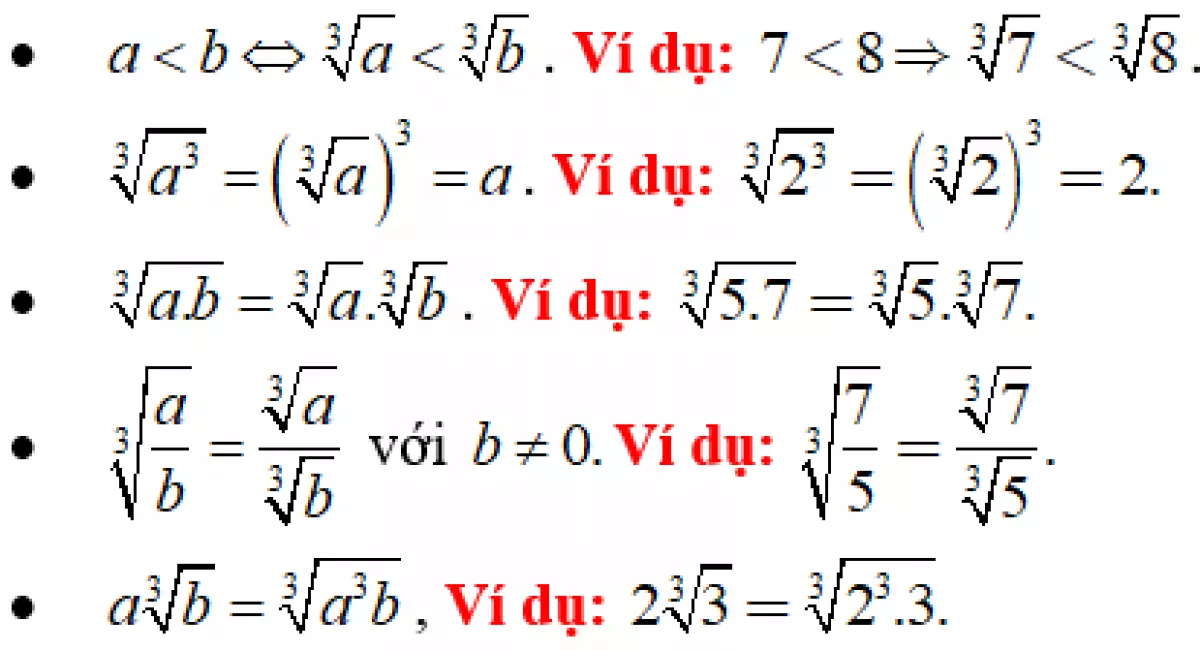Ảnh minh họa: Các tính chất của căn bậc 3
Việc khai căn và áp dụng các tính chất của căn bậc 3 khá đơn giản và không phức tạp như căn bậc 2 do chúng ta không cần phải xét về dấu của giá trị.
4. Áp dụng các tính chất của căn bậc 3
Dựa trên các tính chất đã nêu ở trên, ta có thể áp dụng các quy tắc đưa thừa số vào trong căn hoặc khai căn, các quy tắc khử mẫu của biểu thức lấy căn bậc ba hoặc quy tắc trục căn bậc ba ở mẫu.
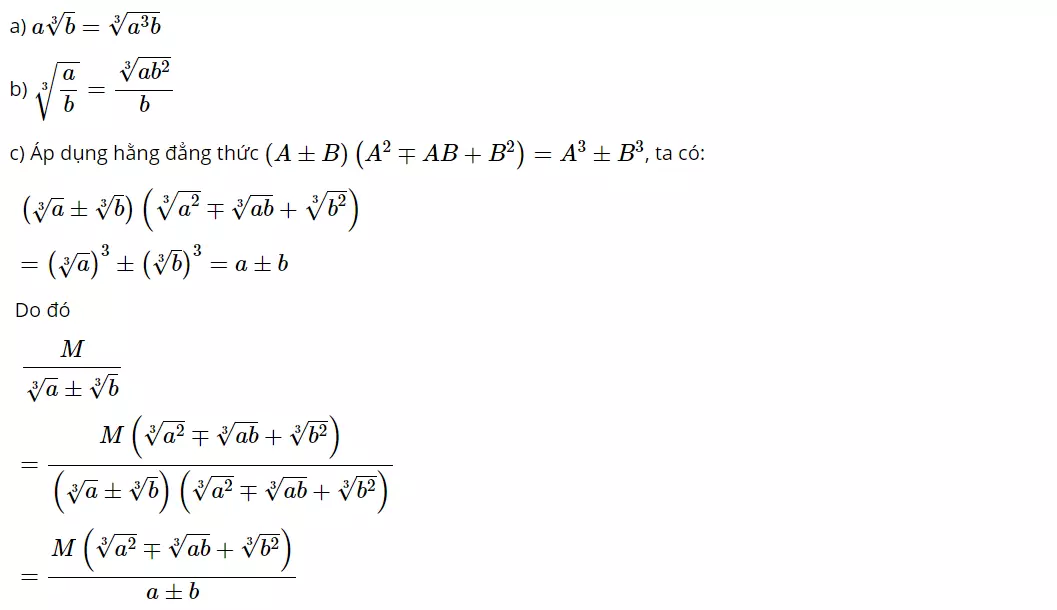
B. Một số dạng bài thường gặp về căn bậc 3
Dạng 1: Tính giá trị căn bậc 3 của số thực, của biểu thức
Để làm được dạng bài này, bạn cần nắm được quy tắc đưa số, giá trị vào trong căn và ra khỏi căn. Dưới đây là quy tắc cụ thể:
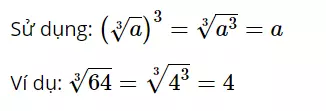
Dạng 2: So sánh các căn bậc 3 với nhau
Khi làm dạng bài này, bạn chỉ cần nhớ quy tắc sau:
Dạng 3: Giải phương trình chứa căn bậc 3
Với dạng bài này, bạn cần áp dụng các quy tắc biến đổi vào căn và sử dụng phương pháp khai căn để tìm giá trị.
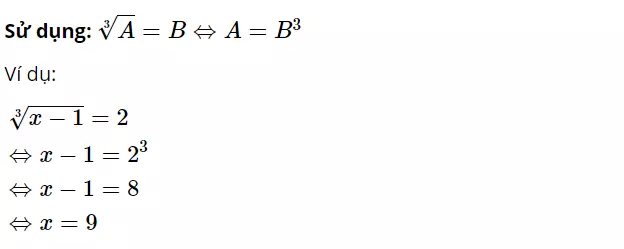
C. Bài tập thực hành về căn bậc 3
Dưới đây là một số bài tập thực hành để bạn ôn tập và củng cố kiến thức về căn bậc 3:
Bài tập 1: Chứng minh giá trị của biểu thức
Bài tập: Hãy chứng minh rằng giá trị của biểu thức sau không bị ảnh hưởng bởi biến:
∛(a³ + 3a² + 3a + 1) = a + 1Hướng dẫn giải:
a³ + 3a² + 3a + 1 = (a + 1)³
∛(a³ + 3a² + 3a + 1) = ∛((a + 1)³)
∛(a³ + 3a² + 3a + 1) = a + 1Bài tập 2: Giải các phương trình
Bài tập: Giải các phương trình sau:
∛(x + 1) + ∛(x - 1) = 2Hướng dẫn giải:
Đặt u = ∛(x + 1) và v = ∛(x - 1)
Ta có hệ phương trình sau:
u + v = 2
u³ + v³ = x + 1 + x - 1 = 2x
Từ đó, ta có:
u³ + v³ = (u + v)(u² - uv + v²) = 2(u² - uv + v²)
Thay u + v = 2 vào, ta có:
2(u² - uv + v²) = 4
u² - uv + v² = 2
Đặt t = uv, ta có:
u² + v² = (u + v)² - 2uv = 4 - 2t
Từ đó, ta có:
u² - uv + v² = 2
4 - 2t = 2
t = 1
Thay t = uv vào, ta có:
uv = 1
∛(x + 1)∛(x - 1) = 1
Giả sử ∛(x + 1) = a và ∛(x - 1) = b, ta có:
a*b = 1
Từ đó, ta có hệ phương trình sau:
a + b = 2
a*b = 1
Giải hệ phương trình này, ta tìm được a = 1 và b = 1.
Vậy:
∛(x + 1) = 1
∛(x - 1) = 1
Từ đó, ta có:
x + 1 = 1
x - 1 = 1
Giải phương trình trên, ta tìm được x = 0.Bài tập 3: Rút gọn các biểu thức
Bài tập: Rút gọn các biểu thức sau:
∛(a³ - 3a² + 3a - 1)Hướng dẫn giải:
Đặt b = ∛(a³ - 3a² + 3a - 1), ta có:
b³ = a³ - 3a² + 3a - 1
Từ đó, ta có:
∛(a³ - 3a² + 3a - 1) = bHy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về căn bậc 3 và áp dụng linh hoạt vào các dạng bài. Chúc bạn học tốt môn Toán và đạt kết quả cao!
Tham khảo thêm: Rút gọn biểu thức chứa căn bậc 2
